火焰参数对辐射图像法不同测温模型的影响

丁永三，秦永新，林 楠，张 彪，许传龙

(1.国家能源集团谏壁发电厂，江苏 镇江 212006; 2.东南大学 能源与环境学院，江苏 南京 210096)

燃烧是最为常见的能源利用形式[1]，在高温工业设备中，如锅炉、燃气轮机、发动机燃烧室等，为了提高燃烧效率和加强燃烧安全防护，通常需要实时监测各项燃烧参数[2]。温度是最重要的热工参数之一，通过对火焰温度分布的实时测量，能够进一步推出火焰中组分的浓度和密度分布，探讨出包括燃烧反应的速率、燃烧产物的生成、燃烧火焰的结构等物理过程和化学机理，全方位了解燃烧过程，进而对火焰燃烧效率做出准确评估[3-4]。实时而准确的火焰温度场检测无论是对能源燃烧的理论研究，还是对预防工业事故、诊断设备故障、优化结构设计等生产实践活动都有着重大的指导意义[5]。

火焰的辐射图像法测温考虑了火焰内部的辐射传输过程，由于火焰燃烧过程中的复杂性，得到更加接近真实的三维火焰温度场分布结果，同时由于测量装置便携易操作、无需外部主动激励(激光、超声等)以及无温度测量上限等优势，该方法在环境条件恶劣的工业现场中的温度测量上有着广阔的发展前景[6-8]。然而，目前的辐射图像火焰温度场测量中通常假定燃烧火焰内部介质的折射率均匀分布，即假定了穿过火焰体的光线传播轨迹可以按直线处理，这样虽然在一定程度上简化了计算过程，提高了计算效率，但在实际工业燃烧中，火焰内部的温度梯度和未燃烧充分的炭黑颗粒，都会导致火焰内部的折射率并不相同[9]。尤其是在内部存在多个高温区的大型燃烧火焰中，如果不考虑由于折射率分布不均带来的光线偏折的影响，将为火焰三维温度场的反演重建带来不可避免的系统误差。

本文结合梯度折射率介质中的辐射传输特点，在传统有限体积法求解的基础上，建立了梯度折射率介质下的火焰辐射成像模型和图像法测温模型，分别针对辐射平衡问题及传热平衡问题，验证了梯度折射率介质下的辐射算法求解结果的正确性，最后分析了火焰尺寸和内部炭黑颗粒浓度对火焰成像和温度场重建的影响特性。

1 梯度折射率下温度辐射测量模型

半透明火焰中除了大多来自碳氢混合物由于燃烧产生的辐射光线，在火焰内部还四散分布着由于燃烧不充分而剩余的炭黑颗粒。相比之下，气相分子由于能级不多、波长受限等原因发出的辐射光线可见程度比较微弱，而在高温火焰中分布的炭黑颗粒可以辐射连续光谱，发出的辐射光线亮度明显更高[10]。在具体的辐射图像测温过程中，半透明火焰中的辐射介质从火焰内部P点发射出的一束辐射光线(如图1所示)，沿不同方向在经历吸收、散射后穿出火焰，到达相机的镜头，光线在主透镜的投射下被图像探测器的某一个像素点全部接收，最终信息被记录后以火焰图像的形式输出。

图1 火焰辐射图像测温原理图

火焰虽然是一个实时变化的动态研究对象，而电磁波的传播速度是光速，对于大多数的火焰，仍然可以把它的成像过程看作一个稳态辐射传输问题，用梯度折射率介质下的稳态辐射传递方程[11]来描述火焰成像过程中内部的辐射传输情况

式中n——介质的折射率;

I(r,Ω)——火焰内r处沿Ω方向的辐射强度;

s——沿Ω方向的距离;

ka和ks——火焰的吸收和散射系数;

Ib(r)——火焰内r处的自身发射强度;

Φ(Ω,Ω′)——沿Ω′方向入射朝Ω方向散射的散射相函数;

Ω′——立体角大小。

对于梯度折射率介质下的火焰辐射传输模型的光线追迹，如图2所示，从P点发出的辐射光线，如果按照均匀介质模型追迹，光线应该沿着虚线箭头的方向传播；而实际传播过程中，由于火焰内部燃烧不充分，残余的炭黑颗粒四散分布导致火焰中的折射率场非均匀分布(n0,n1,n2,…,nm)，光线在传播的过程中不断发生偏折，最终光线的传播方向与假定的均匀介质中光线传播的方向中间偏差了一个θ角，而从火焰中穿出时的位置来看，两者也偏差了一个Δs的距离。

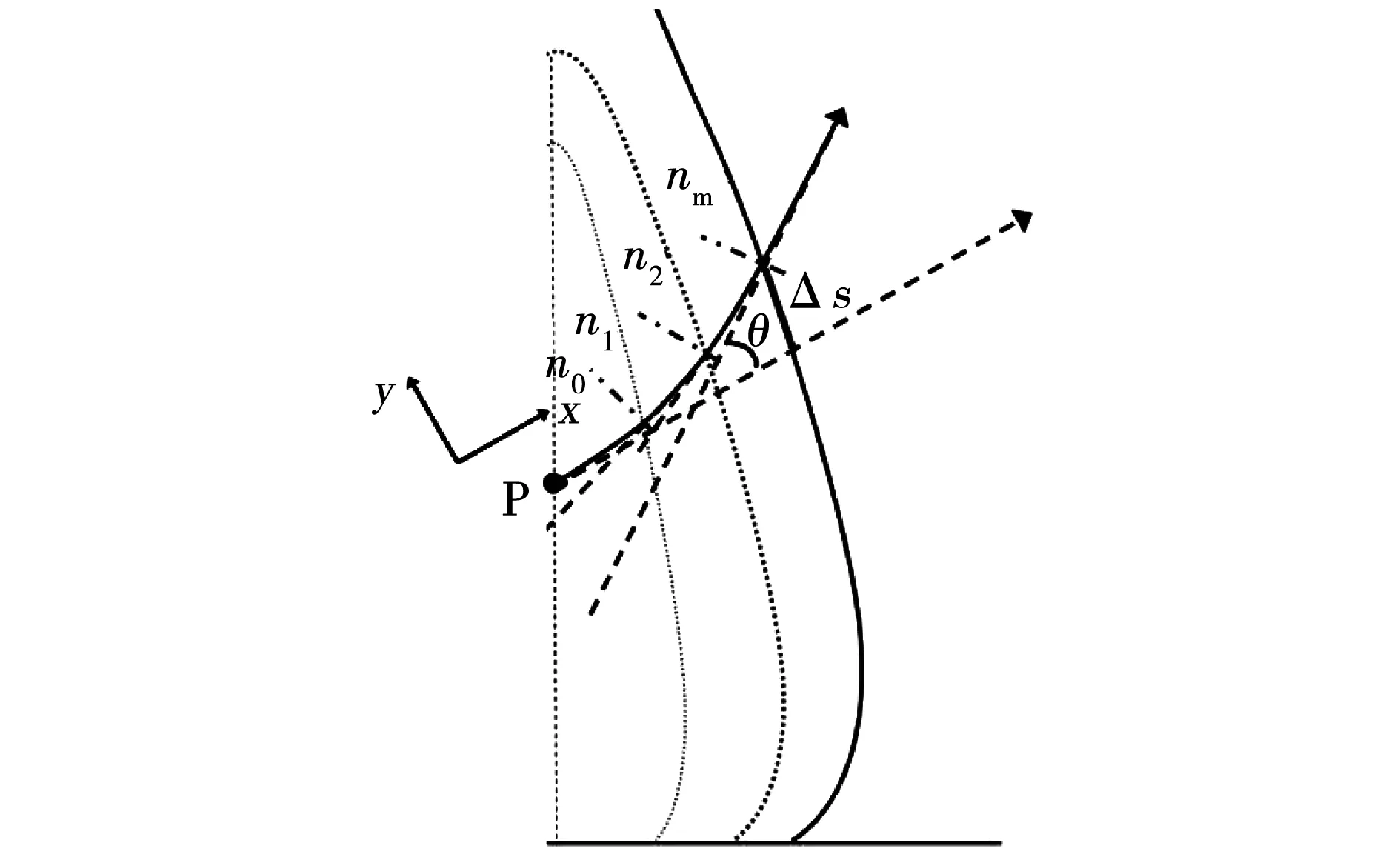
图2 火焰内部由于非均匀介质形成的光线轨迹偏差示意图

根据火焰内部炭黑颗粒的浓度，利用有效介质VAT模型[12]可计算得到火焰每段区间内的有效折射率和吸收系数分布

公式中A、B的数学表达式分别为

B=2ndkdfv+2nckc(1-fv)

式中nd和nc——离散相和连续项的折射率;

φ——分散相的体积分数;

kd和kc——离散相和连续项的吸收系数，气体的吸收系数可由Gladstone-Dale关系式导出，炭黑的吸收系数和散射系数可由Mie理论计算得到。

根据公式(2)和公式(3)在计算出物性参数后，将其代入公式(1)，利用直角坐标系下梯度折射率介质的有限体积法求解火焰内部任意方向的辐射强度I(r,Ω)，根据射线追踪的结果，获得火焰的成像模型

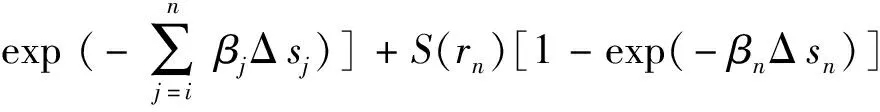
式中S(r)——广义辐射源项，它可由下式来定义[13];

β——衰减系数，β=ka+ks;

Δs——该成像光线穿过当前火焰微元体所经过的路径长度。

根据成像模型获得的线性方程组，利用LSQR反演算法可以重建出广义辐射源项的分布，进而获得火焰自身辐射强度与温度分布。

2 算法验证

2.1 一维平板介质

假设存在一个厚度L=1 m的一维大平板形模型，模型中的介质对辐射具有发射、吸收、散射的性质。如图3所示，平板左右两个壁面的温度分别为T1=1 000 K，T2=1 500 K；壁面发射率ε1=ε2=1；介质的折射率分布为n(z)=1.2+0.6z/L，散射反照率为0，计算光学厚度τL=1.0及τL=3.0下传热平衡时平板间温度分布[14]。

图3 一维半透明平板辐射传递示意图

采用一维坐标系下的有限体积法处理，此处先将该空间沿z轴方向划分为Nz=500个互不重叠的微元段，然后将每个微元段按照角度离散为Nθ=50个辐射方向，计算结果如图4所示。从图中可以看出靠近温度较低的左侧壁面区域，温度变化的梯度较大，且该区域在设定的光学厚度越大的时候，整体温度越低；温度较高的右侧壁面区域则相反，温度变化的梯度较小，且光学厚度越小，整体温度越低。曲线整体与参考文献中的结果吻合得很好。

图4 不同光学厚度下的一维平板介质温度分布结果图

2.2 二维矩形介质

矩形封闭域内充满各向同性散射介质如图5所示，其单向散射反照率ω=1.0，下壁面为热壁面，其它壁面和介质均保持冷0 K(Tw2=Tw3=Tw4=Tg=0 K)。基于矩形封闭域边长L(L=0.1 m)的光学厚度为τL=0.1。矩形域内介质的温度Tg、吸收系数ka与散射系数ks均匀分布，折射率为空间分布为n(x,y)=1+2(x+y)/L，试计算下壁面无量纲壁面热流qw[15]。

图5 二维矩形介质辐射传输模型

此处先将该矩形计算域划分为Nx×Ny=20×20个网格，空间立体角划分为Nθ×Nφ=8×10，计算结果如图6所示。从图中可以看出本文的结果与参考文献的结果吻合得很好。由于折射率的分布不对称，无量纲净辐射热流曲线的形状也是不对称的，这是与均匀折射率介质的情形不同的，从而证明了本文方法的正确性。

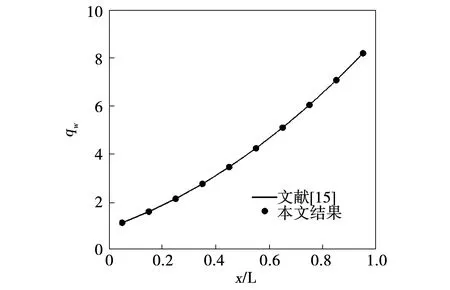
图6 二维矩形介质辐射传输模型热流密度分布结果图

3 结果与讨论

3.1 火焰尺寸对成像的影响

如图7所示，火焰的计算区域为一个长方体，其底面长、高、宽分别为xl，yl和zl，其中yl=3xl=3zl，CCD的探测位置坐标为(0,0,-zl)。将火焰体按x、y、z三个方向划分为10×30×10个控制体；给定的温度T关于火焰体中心轴对称分布，如图8所示，其温度分布和炭黑颗粒浓度分布的数学表述形式如下

图7 火焰尺寸及相机布置示意图

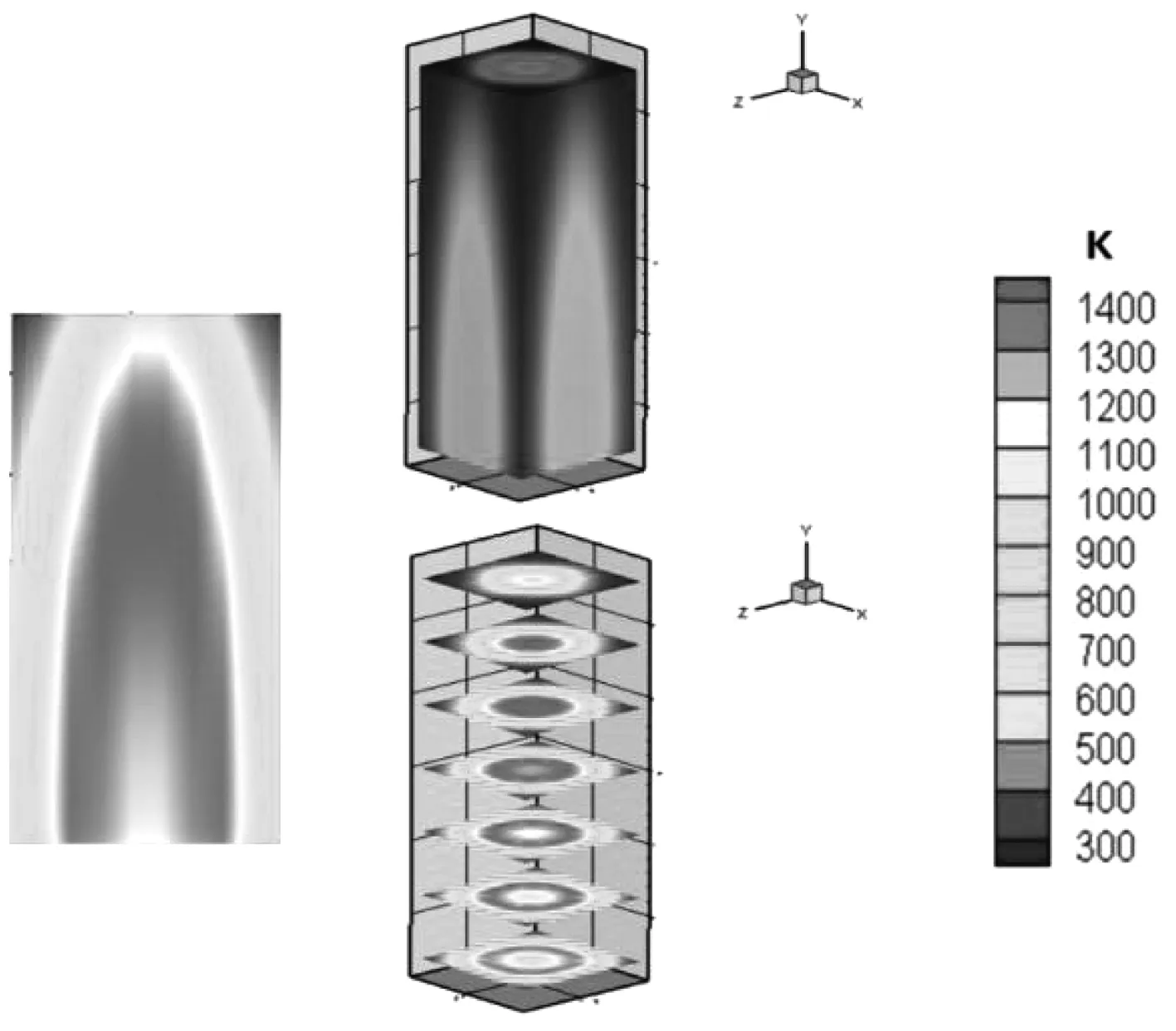
图8 火焰温度场分布示意图

T(x,y,z)=

F(x,y,z)=

火焰成像选用相机的镜头焦距为50 mm，CCD图像探测器的分辨率为720×720，CCD上的像素尺寸为8 μm×8 μm。设定炭黑颗粒浓度Ys=5 ppm，设定三组火焰尺寸，具体的模拟工况如表1所示，成像结果如图9所示。

图9 不同尺寸下的火焰成像

表1 不同尺寸下的火焰工况

比较不同火焰尺寸下的辐射成像结果(如工况A1、B1、C1)，可以看出随着火焰尺寸的增大，火焰图像的亮度呈现出先增强后减弱的趋势。这是由于在CCD探测点与火焰的相对位置不变的情况下，随着火焰尺寸的增大，光在火焰中穿行的距离随之增加，导致火焰的辐射源项对像素点接收到的光强值的增强作用越来越强烈，因此工况B1的图像比工况A1的更加明亮；然而随着火焰尺寸进一步增大，距离CCD较远的控制体发出的光线在穿行的过程中被前面的火焰吸收，导致CCD相机无法捕捉其发出的辐射光线，此时的火焰图像反映的是火焰距离CCD较近的控制体区域的辐射强度信息，但根据温度的设定，外层火焰的温度较低，因此相较于工况C1，工况B1的火焰图像亮度较强。不同模型下光强的计算结果如表2所示。

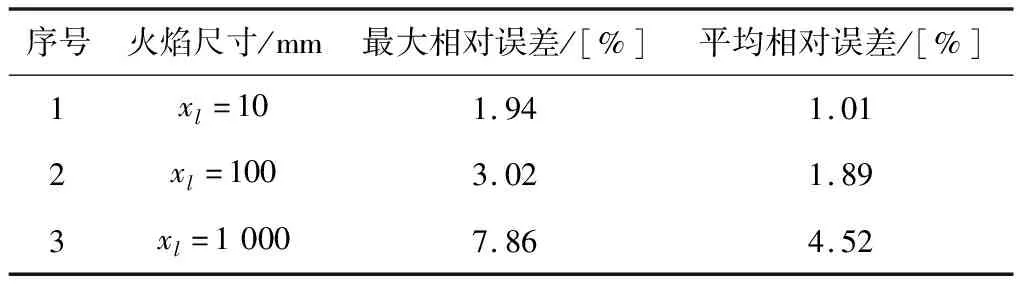
表2 不同模型下辐射强度差值

从表2中的计算结果可以观察到梯度介质辐射模型与均匀介质辐射模型的辐射光强计算结果存在着相对偏差，而且随着火焰尺寸的增大，该偏差也会呈现增加的趋势，在第3组对照中，辐射强度的相对差值最大值达到了7.86%，且该相对差值最大值出现在炭黑颗粒浓度较高的区域附近。一方面，炭黑颗粒浓度越高，该区域的折射率梯度越大，梯度介质辐射模型的计算结果与均匀介质模型的差异就越大；另一方面，随着火焰几何尺寸的增加，其光学厚度也随之增加，火焰源项对其辐射光强值的影响越来越强，导致两种模型下的光强相对差值越来越大。

3.2 炭黑颗粒浓度对温度重建的影响

针对上述火焰，当xl=zl=1 800 mm,yl=5 400 mm；设定的三组炭黑颗粒浓度分别为：Ys=2 ppm、Ys=10 ppm、Ys=50 ppm，CCD的探测位置坐标为(0,-0.5yl,-zl)。将火焰体按x、y、z三个方向划分为10×30×10个控制体，选用相机的镜头焦距为50 mm，CCD图像探测器的分辨率为720 × 720，CCD上的像素尺寸为8 μm×8 μm。其火焰的温度场重建结果如图10～图12所示。

图10 2 ppm时火焰的三维温度场重建结果

图11 10 ppm时火焰的三维温度场重建结果

图12 50 ppm时火焰的三维温度场重建结果

对比以上三组不同炭黑颗粒浓度下的火焰三维温度场重建结果，可以观察到，当炭黑颗粒浓度较小的时候(Ys=2 ppm)，梯度介质下的火焰辐射模型与均匀介质下的火焰辐射模型的重建结果与真实分布比较吻合，两者的相对差值最大值为2.98%，相对差值的平均值为1.14%，这是由于炭黑颗粒浓度较小的时候，火焰的吸收系数也比较小，介质折射率对火焰的三维重建影响并不明显，因此两种辐射模型的火焰三维温度场重建结果都比较好；而当炭黑颗粒浓度增大的时候(Ys=10 ppm)，可以明显看出采用梯度介质辐射模型的火焰三维温度场重建结果依然很好，然而均匀介质辐射模型的火焰三维温度场重建效果已经很不理想，虽然重建出的温度仍与设定温度保持在一个数量级，但几乎分辨不出火焰内部的温度分布，这是由于随着炭黑颗粒浓度的继续增加，火焰的吸收系数也在增大，导致介质折射率对火焰内部的辐射传热和光线传播的影响作用越来越强，此时不能忽视火焰内部折射率的梯度分布；当炭黑颗粒浓度继续加大时(Ys=50 ppm)，可以看到此时两者的火焰三维温度场重建结果都很不理想，均匀介质辐射模型的重建温度已经完全不符合设定的温度分布，而梯度介质辐射模型则只能重建出距离CCD相机探测点较近的火焰控制体的温度分布，这是由于光学厚度过大，距离探测点较远的火焰控制体发出的辐射光线信息已经不能被CCD相机完全捕获。

4 结论

本文建立了梯度折射率介质下的火焰辐射成像模型，验证了梯度折射率介质下的辐射算法求解结果的正确性，在此基础上研究了火焰参数对辐射图像法不同测温模型的影响，得到如下结论：

(1)随着火焰尺寸的增大，火焰图像的亮度呈现出先增强后减弱的趋势，梯度介质模型和均匀介质模型的差异逐渐增强。

(2)当炭黑颗粒浓度较小的时候，梯度介质模型与均匀介质模型的重建结果与真实分布比较吻合，当炭黑颗粒浓度增大的时候，均匀介质模型的火焰三维温度场重建效果已经很不理想。

(3)当炭黑颗粒浓度继续加大时，均匀介质模型的重建温度已经完全不符合设定的温度分布，而梯度介质辐射模型则只能重建出距离CCD相机探测点较近的火焰控制体的温度分布。