The Centroids of the Lie Algebra W(a,b)

SHI Chenmiao, GAO Shoulan

(1.School of Science, Huzhou University, Huzhou 313000, China;2.Department of Mathematics, Shanghai Normal University, Shanghai 200234, China)

Abstract：The Lie algebra W(a,b) is an important infinite dimensional Lie algebra both in Mathematics and Physics. The centroid of Lie algebra has close relationship with derivations and the Poisson algebra structure. By using the grading and ad-semisimple element in this paper we determine the centroids of the Lie algebra W(a,b) and its central extensions, which is helpful to determine the centroids of other Lie algebras.

Keywords：Lie algebra W(a,b); centroid; central extension

0 Introduction

For two complex numbersa,b,the Lie algebraW(a,b) is an infinite dimensional vector space with a basis {Lm,Im|m∈} over the complex fieldsatisfying the following brackets:

[Lm,Ln]=(m-n)Lm+n, [Lm,In]=-(n+a+bm)Im+n, [Im,In]=0

for allm,n∈[1]. The subalgebraW=⊕m∈Lmis the Witt algebra andJ=⊕m∈Imis the tensor density module ofW. The Lie algebraW(a,b) plays an important role in many fields of mathematics and physics. The twisted Heisenberg-Virasoro algebra[2]and the W(2,2) algebra[3]are both central extensions of the Lie algebraW(a,b). The Lie algebraW(a,b) and its central extensions have been extensively studied, such as [1]～[5].

The centroid of a Lie algebraL, denoted by Cent(L), is the space ofL-module homomorphismsχonL:χ([x,y])=[x,χ(y)] for allx,y∈L(viewingLas anL-module under the adjoint action)[6]. The centroid has close relationship with derivations and the Poisson structure of Lie algebra. So the centroid is an ingredient part in the theory of Lie algebras. In this paper, we will determine the centroids of the Lie algebraW(a,b) and its central extensions.

Throughout this paper, we denote byandthe set of integers and the set of complex numbers, respectively. All the vector spaces are assumed over the complex field, andidis the identity transformation of the vector space.

1 The centroid of the Lie algebra W(a,b)

NoteJis the maximal proper ideal of the Lie algebraW(a,b), thenχ(Im)∈Jfor anyχ∈Cent(W(a,b))[7].

Theorem1 Up to isomorphism, the centroid of the Lie algebraW(a,b)

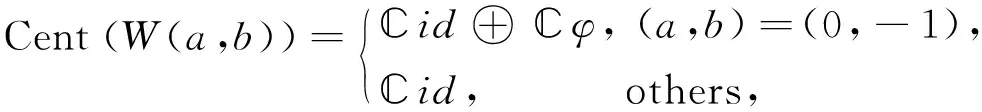
whereφ∈Cent(W(a,b)) defined as follows:

φ(Lm)=Im,φ(Im)=0,m∈.

ProofFor anyχ∈Cent(W(a,b)), assume

χ(Lm)=∑amiLmi+∑bmjImj,χ(Im)=∑gmlIml.

Usingχ([L0,Lm])=[L0,χ(Lm)] andχ([L0,Im])=[L0,χ(Im)],we have

-∑miamiLmi-∑(mj+a)bmjImj=-m(∑amiLmi+∑bmjImj),

-∑(ml+a)gmlIml=-(m+a)∑gmlIml.

Then we get the following identities:

miami=mami， (mj+a)bmj=mbmj，

(1)

(ml+a)gml=(m+a)gml.

(2)

Case1a∈. SinceW(a+kb,b)≅W(a,b) for anyk∈[1], we only need to considera=0. From (1)～(2), we can see thatmi=ml=m,mj=m-a=mifami≠0,bmj≠0,gml≠0.So

χ(Lm)=amLm+bmIm,χ(Im)=gmIm.

Usingχ([Lm,Ln])=[Lm,χ(Ln)], we can get

(m-n)am+nLm+n+(m-n)bm+nIm+n=(m-n)anLm+n-(n+bm)bnIm+n.

Then

an=am+n,m≠n,

(3)

-(n+bm)bn=(m-n)bm+n.

(4)

Takem=-n,n≠0 in (3), then we haveam=a0for allm∈. So

χ(Lm)=a0Lm+bmIm.

(5)

Since [Im,L0]=mIm, we have

mχ(Im)=χ[Im,L0]=[Im,χ(L0)]=[Im,a0L0+b0I0]=ma0Im.

Hence

χ(Im)=a0Im,m≠0.

Using [L1,I-1]=(1-b)I0, we get

(1-b)χ(I0)=χ[L1,I-1]=[L1,χ(I-1)]=[L1,a0I-1]=a0(1-b)I0.

Ifb≠1, we haveχ(I0)=a0I0. Ifb=1, using [L1,I0]=-I1, we can obtain

-a0I1=-χ(I1)=χ[L1,I0]=[L1,χ(I0)]=[L1,g0I0]=-g0I1.

Sog0=a0, which showsχ(I0)=a0I0. Therefore, fora=0, we always have

χ(Im)=a0Im,m∈.

(6)

Letn=0 in (4), then we can get

bm=-bb0,m≠0.

(7)

Letn=-m≠0 in (4), then we have

(1-b)bm=2b0,m≠0.

(8)

Using (7), we obtain

(b-2)(b+1)b0=0.

(9)

Subcase1b≠-1,2. Then we haveb0=0 via (9) andbm=0 for allm∈by (7). By (5) and (6), we have

χ(Lm)=a0Lm,χ(Im)=a0Im,m∈.

Subcase2b=-1. Using (8), we havebm=b0for allm∈. By (5) and (6), we have

χ(Lm)=a0Lm+b0Im,χ(Im)=a0Im,m∈.

Subcase3b=2. By (7), we havebm=-2b0form≠0. Letm=2,n=1 in (4), it is easy to seeb0=0. Thenbm=0 for allm∈. Hence, by (5) and (6),

χ(Lm)=a0Lm,χ(Im)=a0Im,m∈.

Case2a∉. Thenmj≠m-afor anymj,m∈. By (1), we havebmj=0. Using (1)～(2), we getmi=ml=mifami≠0,gml≠0. So

χ(Lm)=amLm,χ(Im)=gmIm,m∈.

Byχ([Lm,Ln])=[Lm,χ(Ln)], we have

(m-n)am+nLm+n=(m-n)anLm+n.

So

(m-n)an=(m-n)am+n.

(10)

Similar to Case 1, we haveam=a0for allm∈. Henceχ(Lm)=a0Lmfor allm∈. Using [Im,L0]=(m+a)Im, we have

(m+a)χ(Im)=χ[Im,L0]=[Im,χ(L0)]=[Im,a0L0]=(m+a)a0Im.

Sincea∉, we havem+a≠0 for allm∈. Henceχ(Im)=a0Imfor allm∈. Therefore,

χ(Lm)=a0Lm,χ(Im)=a0Im,m∈.

2 The centroids of the central extensions of the Lie algebra W(a,b)

The second cohomology groupsH2(W(a,b),) were determined in Theorem 2.3 in [1]. Hence the central extensions of the Lie algebraW(a,b) are all known. Up to isomorphism, the Lie algebraW(a,b) has universal central extension except(a,b)≠(0,1). In this section, we determine the centroids of Vir(a,b), which is the universal central extension of the Lie algebraW(a,b).

2.1 The centroid of the twisted Heisenberg-Virasoro Lie algebra

The twisted Heisenberg-Virasoro Lie algebraHVis the universal central extension ofW(0,0).HVhas a basis {Lm,Im,CL,CLI,CI|m∈} satisfying the following relations:

[Lm,In]=-nIm+n+(m2+m)δm+n,0CLI,

[Im,In]=mδm+n,0CI, [CL,HV]=[CLI,HV]=[CI,HV]=0

for allm,n∈.

HVhas a natural-grading:HV=⊕n∈HVn, where

HVn={x|adL0(x)=-nx,x∈HV},∀n∈.

Using the Lie bracket ofHV, we can see that

HVn=span{Ln,In,δn,0CL,δn,0CLI,δn,0CI},∀n∈.

Theorem2 The centroid of the twisted Heisenberg-Virasoro Lie algebra

Cent(HV)=id.

ProofLetχ∈Cent(HV). Sinceχ[L0,x]=[L0,χ(x)]=adL0(χ(x)), for anyx∈HVn, wheren∈, we have adL0(χ(x))=-nχ(x). Soχ(x)∈HVn, that is,χ(HVn)⊆HVn.

Assume

χ(Lm)=amLm+bmIm+δm,0λCL+δm,0μCLI+δm,0νCI,

χ(CL)=x11CL+x12CLI+x13CI.

Byχ([Lm,Ln])=[Lm,χ(Ln)], we have

(m-n)[am+nLm+n+bm+nIm+n+δm+n,0λCL+δm+n,0μCLI+δm+n,0νCI]+

According to the coefficients ofLm+n,Im+n,CL,CLI,CI, we can obtain

Then we can getam=a0,bm=0,λ=μ=ν=0,x11=a0,x12=x13=0 for allm∈. Therefore,χ(Lm)=a0Lm,χ(CL)=a0CLfor allm∈.

Similar to Case 1 in Theorem 1, we can obtainχ(Im)=a0Imfor allm∈.

Furthermore, byχ([L1,I-1])=[L1,χ(I-1)], we have

a0I0+2χ(CLI)=a0I0+2a0CLI.

Soχ(CLI)=a0CLI. Moreover,

χ(CI)=χ([I1,I-1])=[I1,χ(I-1)]=[I1,a0I-1]=a0CI.

Therefore, Cent(HV)=id, where id is the identity transformation ofHV.

2.2 The centroid of the Lie algebra W(2,2)

The Lie algebra W(2,2), denoted byL, is the universal central extension ofW(0,-1).Lhas a basis {Lm,Im,CL,CLI|m∈} satisfying the following relations:

[Im,In]=0, [CL,L]=[CLI,L]=0

for allm,n∈.

Lhas a natural-grading:L=⊕n∈Ln, where

Ln={x|adL0(x)=-nx,x∈L},∀n∈.

Using the Lie bracket ofL, we can see that

Ln=span{Ln,In,δn,0CL,δn,0CLI},∀n∈.

Theorem3 The centroid of the Lie algebra W(2, 2)

Cent(L)=id⊕

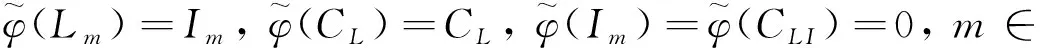
(11)

ProofFor anyχ∈Cent(L), similar to Theorem 2, we haveχ(Ln)⊆Lnfor alln∈. Then we can assume

χ(Lm)=amLm+bmIm+δm,0λCL+δm,0μCLI,χ(CL)=x11CL+x12CLI.

For anym,n∈, byχ([Lm,Ln])=[Lm,χ(Ln)], we can get

Hence, we have

am+n=an,bm+n=bn,m≠n,

It is easy to get thatam=a0,bm=b0for allm∈andλ=μ=0,x11=a0,x12=b0. Henceχ(Lm)=a0Lm+b0Im,χ(CL)=a0CL+b0CLIfor allm∈. Similar to Case 1 in the proof of Theorem 1.1, we can obtainχ(Im)=a0Imfor allm∈.

Usingχ([L2,I-2])=[L2,χ(I-2)], we can get

2.3 The centroid of the universal central extension of

[Im,In]=(2m+1)δm+n,-1CI, [CL,SV]=[CI,SV]=0

for allm,n∈[5].

Similar to the proof of the cases above, we can get the following result.

Theorem4Cent(SV)=id.

2.4 The centroid of the universal central extension of other cases

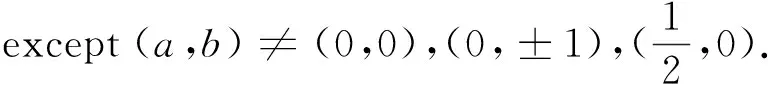
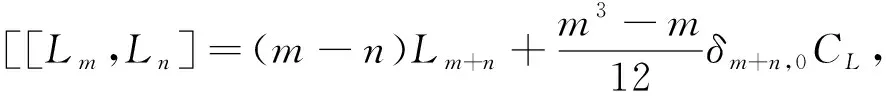
[Lm,In]=-(n+a+bm)Im+n,

[Im,In]=0, [CL,G]=0

for allm,n∈.

Theorem5Cent(G)=id.

ProofLetχ∈Cent(G). Assumeχ(L0)=∑aiLi+∑bjIj+λCL.

Since 0=χ([L0,L0])=[L0,χ(L0)], we have

0=[L0,∑aiLi+∑bjIj+λCL]=-∑iaiLi-∑(j+a)bjIj.

Then

iai=0, (j+a)bj=0.

(12)

Obviously,ai=0 fori≠0.

Case1a∉. Thenj+a≠0 for anyj∈. By (12), we havebj=0. So

χ(L0)=a0L0+λCL.

Form≠0, usingmχ(Lm)=χ([Lm,L0])=[Lm,χ(L0)], we have

mχ(Lm)=[Lm,a0L0+λCL]=ma0Lm.

Soχ(Lm)=a0Lmfor allm≠0. Since

2χ(L0)=χ([L1,L-1])=[L1,χ(L-1)]=[L1,a0L-1]=2a0L0,

we haveχ(L0)=a0L0. Therefore, we obtain

χ(Lm)=a0Lm,∀m∈.

Henceχ(CL)=a0CL.

Using [In,L0]=(n+a)In, we have

(n+a)χ(In)=χ([In,L0])=[In,χ(L0)]=[In,a0L0]=(n+a)a0In.

Sincen+a≠0 for alln∈, we have

χ(In)=a0In, ∀n∈.

Therefore,χ=a0id.

Case2a∈. Up to isomorphism, we only need to considera=0 andb≠0,±1. Thenbj=0 forj≠0 via (12). So

χ(L0)=a0L0+b0I0+λCL.

Form≠0, usingmχ(Lm)=χ([Lm,L0])=[Lm,χ(L0)], we have

mχ(Lm)=[Lm,a0L0+b0I0+λCL]=m(a0Lm-bb0Im).

Hence

χ(Lm)=a0Lm-bb0Im,m≠0.

Since

2χ(L0)=χ([L1,L-1])=[L1,χ(L-1)]=

[L1,a0L-1-bb0I-1]=2a0L0+b(b-1)b0I0,

we have

2a0L0+2b0I0+2λCL=2a0L0+b(b-1)b0I0.

Soλ=0 and 2b0=b(b-1)b0, which shows (b-2)(b+1)b0=0. Becauseb≠-1, we have

(b-2)b0=0.

(13)

Subcase1b≠2. Then we getb0=0 via (13). Hence

χ(Lm)=a0Lm, ∀m∈.

Henceχ(CL)=a0CL.

Using [In,L0]=nIn, we have

nχ(In)=χ([In,L0])=[In,χ(L0)]=[In,a0L0]=na0In.

Henceχ(In)=a0Inforn≠0. In addition,

(1-b)χ(I0)=χ([L1,I-1])=[L1,χ(I-1)]=[L1,a0I-1]=(1-b)a0I0.

Notice thatb≠1, then we getχ(I0)=a0I0. So

χ(In)=a0In,n∈.

Therefore,χ=a0id.

Subcase2b=2. Then

χ(L0)=a0L0+b0I0,χ(Lm)=a0Lm-2b0Im,m≠0.

Notice that the center of this Lie algebra isCL, then we can assumeχ(CL)=ρCL.

ThenρCL=a0CL+8b0I0. Therefore,b0=0 andρ=a0. Then

χ(Lm)=a0Lm,χ(CL)=a0CL, ∀m∈.

Using [In,L0]=nIn, we have

nχ(In)=χ([In,L0])=[In,χ(L0)]=[In,a0L0]=na0In.

Henceχ(In)=a0Inforn≠0. In addition,

χ(I0)=χ([I-1,L1])=[I-1,χ(L1)]=[I-1,a0L1]=a0I0.

Soχ(In)=a0Infor alln∈.

Therefore,χ=a0id. The theorem holds.