列表分析法在初中数学教学中的应用探究

林赞娟

【摘要】数学问题中信息（条件）的读取与分析，每一个信息的内在关联与因果关系，信息所能延伸的最近结论与重构生长结论，都是学生在解决问题中的难点。本文选取人教版初中数学课本中部分应用问题与规律探究问题，阐述了列表分析法的构建、教学应用与实质性价值.

【关键词】列表分析法;核心素养;实际应用;规律探究

一、问题提出

第一，课标与数学核心素养。一是《数学课程标准》总目标中提到“问题解决”，明确指出：使学生综合运用数学知识解决简单的实际问题，增强应用意识，获得分析问题和解决问题的一些基本方法，体验解决问题方法的多样性;二是数学核心素养包括数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析六个方面。通过列表法，培养学生思维的缜密性和有序性，有助于提高学生的数学建模、数据分析能力;三是解决问题的方法就是解决问题的核心，其中“列表法”就是应用广泛且有效的一种分析问题的方法，它在信息量较大、数量关系较为复杂的问题中有非常明显的优越性。

第二，中考命题与考试情况反馈（以广州市为例）。从广州市近几年的中考中，发现应用题的得分并不高，每年有15%的考生直接放弃，得0分，主要原因：审题类错误：对条件或问题信息的提取不全面或无法提取信息，不能将实际问题抽象为常见的应用型问题模型;思维类错误：知识缺漏，分析、整理条件能力弱，找不到等量关系;计算类错误。

第三，教学情况反馈。一是应用题的学习是初中生的一大难点。如对两个班学生进行学习应用题的问卷调查，两个班84名学生，有近一半40名学生选择一般，有20名学生选择较差，还有10名学生选择很差。二是规律探究问题。规律探索题是数学发现过程的一种创造思维。规律探索题成为许多省市中考題的热点，这类题大都作为“小压轴题”出现在选择、填空的最后一题，具有较强的选拔性。这类问题基本上是学生的难点。

二、问题思考

第一，列表分析法概念的内涵。列表分析法是将问题中的数量以表格的形式呈现，通过表格分析数量之间的关系或规律，从而构建合适的等量关系（或不等关系），进一步建立方程（不等式）。

第二，列表分析法在初中数学中的基本应用。列表法在初中数学中的应用主要体现在以下四大领域：构建方程（不等式）解实际问题、数与式及图形中探索规律问题、概率问题、函数问题。七年级列一次方程（不等式）、八年级列分式方程、九年级列一元二次方程来解实际问题，是这四个领域中用列表分析法最多的一块。

第三，列表分析法的教学意义。一是列表分析法能够为学生建构一种基于解决课本核心问题的方法与能力，形成其基本的数学素养，包括建模意识与能力，数据分析能力等;二是列表分析法能力的形成，可以延伸到其它问题的研究方法，以及初高中数学能力的衔接，对高中数学的学习在思想方法打下基础.

三、问题解决

第一，列表分析法的教学实践。一是应用问题类。解应用题的一般步骤是：“审、设、列、解、验、答” 。六个步骤里面，“审”是最难的一个步骤，突破此难点可用列表法。列表法的步骤：①分析问题：找出基本量，把它作为表格的“行”，而“列”通常表示量与量之间的比较;②列表填空：把已知量和未知量填入表格;③找等量关系列方程，如例1;二是规律探究问题类，如例2。

例1（人教版七年级下册P100例2）：

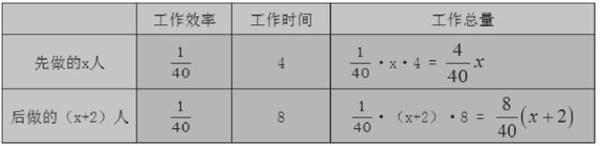
整理一批图书，由一个人做要40 h完成。现计划由一部分先做4 h，然后增加2人与他们一起做8 h，完成这项工作;假设这些人的工作效率相同，具体先安排多少人工作？

①审题-构建表格

表格的“行”：三个基本量，工作效率，工作时间、工作总量。

表格的“列”：两者的比较可以是先做的x人和后做的（x+2）人。

②列表填空

设先安排x人工作。

列出表格：

③等量关系：先做的x人的工作量+后做的（x+2）人的工作量 =工作总量1。强调：工程问题中，如果没有具体指出工作总量是多少时，工作总量通常设为单位1。

④列出方程：

例2（人教版七年级P43）：

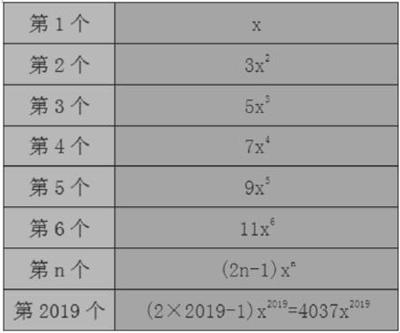
观察下列关于x的单项式，探究其规律：x，3x2，5x3，7x4，9x5，11x6，……。按照上述规律，第2019个单项式是什么？

列表分析数据：

通过列表的方法整理分析数据，简单清晰可见这个单项式的系数就是一个奇数数列，从而归纳出第n项的规律，进而求出第2019个单项式的表达。

第二，列表分析法的实践性效果。一是在解决应用题与规律问题中的意义。列表分析法可以引导学生寻找题中各种量之间的联系，降低了问题的难度，对培养学生学习兴趣、提高学生学习成绩、提升学生的思维能力都有很大帮助。如曾在讲评人教版八年级数学下册P153的例4的这道应用题时：某次列车平均提速 v km/h，用相同的时间，列车提速前行驶 s km，提速后比提速前多行驶 50 km，提速前列车的平均速度为多少？在自己所任教的两个班，分别用不同的方法讲评这道题，一个班用传统的方法讲，另一个班用列表法讲。讲完后，让这两个班同时测验课文P155第8题的一部分。题目：两个小组同时开始攀登一座高为h 米的山，第一组的攀登速度是第二组的a倍，并比第二组早t 分钟到达顶峰，则两组的攀登速度各是多少？结果显示，传统方法讲解班级（42人）做对题目13人;列表法讲解班级（42人）做对题目31人。二是能力的迁移。学生掌握列表分析法，能实现能力的正迁移，在函数列表法、概率列表法中会掌握得更好，对学生在高中用列表分析数列也是一种能力上的储备。三是存在的主要问题。不能准确完整地构建表格，行与列如何设计，分别填哪些量，学生有难度。

列表分析法作为解决问题的高效方法，目的是帮助学生分析问题。但在实际教学中，必然会遇到一些学生，他们提炼信息和建立模型的能力都很强，无需列表便可解题，列表对他们来说是没有必要的，千万不可为了列表而列表，否则这就有违运用列表法解题的初衷了。

参考文献：

[1] 潘军.列表学习法在初中数学中的作用探究[J].时代教育，2015（04）.

[2] 董杰玲.运用列表法解决问题，引导学生有序思考[J].掌桥科研，2016.

[3] 凌娟，吴高平.关于列表法解决问题的思考和初探[J].爱学术，2014（12）.