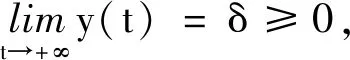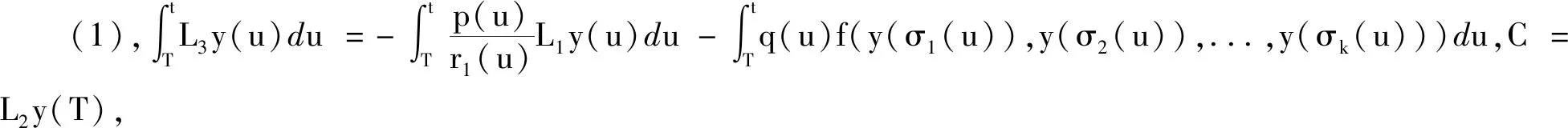三阶时滞泛函微分方程的振动性

侯晓磊

山西工商学院计算机信息工程学院，山西 太原 030006

文献[1]研究了方程((r2(t)r1(t)y′)′)′+p(t)y′+q(t)f(y)=0，利用广义Riccati变换建立了该方程至少存在一个振动解的充分条件.文献[2]进一步研究了形式为((r2(t)r1(t)y′)′)′+p(t)y′+q(t)f(y(g(t)))=0的三阶非线性时滞微分方程的振动性.文献[3]研究了

(a)r1,r2∈C[T0,+∞),r1>0,r2>0;

(b)q∈C[T0,+∞),q(t)≥0且当t趋于无穷大时q(t)≠0;

(c)p∈C1[T0,+∞),p(t)≥0;

(e)f∈C1(-∞,+∞)∩C1(-∞,0)∩C′(0,+∞),uf(u)>0,f′(u)≥0(u≠0);

在以上研究的基础上，本文讨论的是下列三阶时滞泛函微分方程的振动性

(r2(t)(r1(t)y′(t))′)′+p(t)y′(t)+q(t)f(y(σ1(t)),y(σ2(t)),...,y(σk(t)))=0t≥T0

(1)

这里T0>0，此方程满足下列条件：

(a)r1,r2∈C[T0,+∞),r1>0,r2>0;

(b)q∈C[T0,+∞),q(t)≥0且当t趋于无穷大时q(t)≠0;

(c)p∈C1[T0,+∞),p(t)≥0;

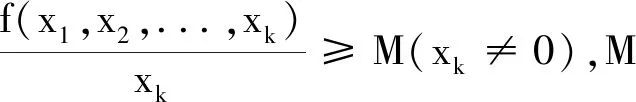
1 准备工作

引理1 假设

(2)

是非振动的,如果y(t)是方程(1)的一个非振动解,那么如果存在一个T1≥T0,对于所有的t≥T1,有y(t)L1y(t)>0或y(t)L1y(t)<0.

证明 设y(t)是方程(1)的一个最终正解,存在一个T1≥T0对于所有的t≥T1时,总有y(t)>0,y(σi(t))>0(σi(t)≥T1).显然x(t)=-L1y(t)是二阶非齐次微分方程

(3)

的解.下证方程(3)的所有是非振动的.令z(t)是(2)式的一个解,z(t)>0.设x(t)是方程(3)的一个解，如果它有两个相邻的零点b,c(b0,t∈(b,c),x′(b)≥0,x′(b)≤0,并有

(4)

(5)

将(2)式乘以x(t)减去(3)式乘以z(t)有

x(t)(r2(t)z′(t))′-z(t)(r2(t)x′(t))′=-q(t)z(t)f(y(σ1(t)),y(σ2(t)),...,y(σk(t)))=0

即

r2(t)(x(t)z′(t))-(x′(t)z(t))′=-q(t)z(t)f(y(σ1(t)),y(σ2(t)),...,y(σk(t)))=0

(6)

将(6)式从b到c积分得

矛盾,所以对于所有的t≥T1,有y(t)L1y(t)>0或y(t)L1y(t)<0.

(7)

若y(t)是方程(1)的一个非振动解,并且当t充分大时,有y(t)L1y(t)≥0,那么存在一个T2≥T1,使得对于所有的t≥T2时有

L0y(t)Lky(t)>0k=0,1,2L0y(t)L3y(t)≤0

(8)

证明y(t)是方程(1)的一个非振动解,我们不妨设y(t)>0,显然

L0y(t)L0y(t)=y2(t)>0L0y(t)L1y(t)=y(t)L1y(t)>0

由L3y(t)≤0知L2y(t)是递减函数,不妨设L2y(t)≤0,那么存在一个正数M1，使

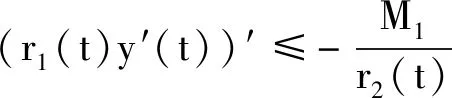
(9)

(10)

易证每个具有V2性质的非振动解y(t)是无界的.

p2′(t)≥0φ(t)≥0φ′(t)≥0

(11)

(12)

2 主要结果

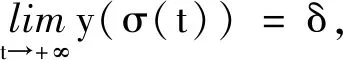
其中,C=L2y(T),得L2y(t)<0.矛盾.