基于事件触发的二阶随机时延系统的有限时间一致

崔艳，王晓珊

山西师范大学物理与信息工程学院，山西 临汾 041000

多智能体由于具有自主性、分布性、协调性等特点，被广泛应用于许多科学研究，包括一致性问题[1～3]，编队控制[4]，模拟动物集群[5]，智能体的蜂拥等问题.但是从资源利用角度看，当系统达到一致时，保持数据的状态不再进行更新，就可以减少系统更新的次数，不会造成通信信道的负担.于是基于事件触发的控制策略得以发展，文献[6]提出了一种事件触发的分布式同步控制算法，Jiang等人采用反馈控制研究了一系列非线性系统的一致性问题.文献[7]中，Xie等人利用每一个跟随者的事件触发线性反馈律来设计控制更新协议，解决了多智能体的全局领导跟随控制问题.文献[8]中，由Zhang等人改进的集中式和分布式事件触发函数被用来解决领导跟随系统网络的一致性问题.以上文献研究的都是基于事件触发的多智能体系统的一致性.

除了对通信信道的更新次数的研究外，对于信道因为数据传输慢或者拓扑网络变化而造成输入数据的延迟，对系统的影响也较大，这也是研究者们关注的一个重点.已经有文献研究了带有时滞的多智能体系统的一致性[9～11]，文献[9]采用频域分析法研究了定拓扑网络下有领导者的二阶时滞系统的一致性问题，并计算出所允许的最大时滞.而文献[10]研究了混合阶多智能体系统的组一致性问题，利用模型转换，将闭环系统转化为等价系统，利用一系列的理论推导得出了系统到达组一致性的充分条件.随机时滞多智能体系统的研究作为随机多智能体系统一致稳定性分析的一部分在文献[11]中呈现.

以上文献都是针对多智能体系统一致性进行研究的，但是一些实际系统，要求系统在有限时间内达到一致，这样才能精确的应用到人工智能，无人机飞行控制[12]，智能机器人机械臂的协调控制[13,14]等实际中.因此，本文不仅借助事件触发策略，研究了二阶多智能体系统的有限时间一致，而且对实际应用中存在的时延问题也进行了讨论，同时对于芝诺现象的排除也给出了具体的证明过程.

本文的主要结构如下：第一部分是文章的基础知识、一些基本的理论和必要的引理.第二部分是所设计的非线性协议和触发条件.第三部分是一些例子及仿真的结果.最后一部分给出的是结论及今后要做的工作.

1 基础知识和问题描述

1.1 基础知识

1.2 问题描述

加权无向通信拓扑G(V,E,A)，每个智能体可视为拓扑图中的顶点，智能体之间的信息传输可视为图的边，具有跟随者和领导者的二阶多智能体系统的动态模型如下：

(1)

其中，Xi(t)、Vi(t)、U(t)分别是智能体的位置状态、速度状态和控制输入.x0(t),v0(t)是领导者的状态，并且Vit(s)=Vi(t+s)

定义1 有限时间一致：多智能体系统(1)称为有限时间一致，如果存在一个确定时间T0∈[0,+∞)，使得每一个智能体的状态满足以下等式：确定允许每个智能体的状态满足以下条件：

并且对于任意的t≥T0都满足Xi(t)-X0(t)→0,Vi(t)-V0(t)→0,i,j∈I.

定义2[ 15]考虑系统

(2)

其中，f(x)=(f1(x),f2(x),...,fn(x))T是一个连续的向量场.如果对于任意的f(x)都有fi(εr1x1,εr2x2,...,εrnxn)=εk+rifi(x),ε>0,i∈1,2,...,n,∀x∈Rn则f(x)是带有扩张(r1,r2,...,rn)的度k(k∈R)的齐次性.

如果系统的向量场是齐次的，则该系统就是齐次的.

定义3[15]此外，考虑以下系统

(3)

(4)

其中，ri是系统状态变量xi对应的权重.

引理1 如果系统是齐次的，并且是局部渐近稳定的，则系统是全局渐近稳定的.这个性质同样适用于有限时间稳定.

引理2 考虑下列系统

其中，X(t),V(t),U(t)∈Rn，a,bk,τk是正的常数.

现在系统(1)具体表示为如下形式：

+β1sig(Xj(t)-Xi(t))α1+β2sig(Vj(t)-Vi(t))α2

-bisig(Xi(t-τk)-X0(t-τk))α1-bisig(Vi(t-τk)-V0(t-τk))α2

应用引理2，系统可以转换为如下形式：

2 主要结果

定义智能体i的位置测量误差定义为

(5)

智能体i的速度测量误差表示为

(6)

(7)

因此，我们得到：

(8)

因此可以得到

(9)

其中，

(10)

本文所采用的协议是分布式控制协议，它不仅可以有效地降低智能体之间的连通强度，同时可以降低智能体的触发次数.下面研究的是控制协议在拓扑网络中的有限时间一致.

引理3 相似于参考文献[15]的分析，如果系统(9)是渐近稳定的，且带有扩张(2,2,...,2|α1+1,α2+1,...,αn+1)的度k=α1-1<0是齐次的，则系统可以在有限时间内达到一致.

智能体i的触发条件表示如下：

(11)

其中，M,N是确定的正常数.

定理1 对于系统(9)中的无向连通网络拓扑图，结合事件触发条件(11)，使得系统在控制协议(7)作用下实现具有随机时延的二阶系统限时间一致.

证明 构造候选李雅普诺夫函数

对V(t)进行求导，

则

(12)

因为

(13)

结合事件触发条件得到

所以

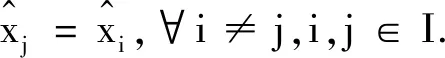
根据LaSalle’s的不变原理，系统(9)是渐近稳定的.即，当t→+∞，有xi-x0→0;vi-v0→0,∀i∈I.

接下来要证明的是系统有负的齐次度并且满足等式(4).控制协议改写成为u=u1+u2,

其中,R1=r1+β1,R2=r2+β2.

而且

接下来，证明事件触发引起的芝诺现象可以排除.芝诺现象指的是在有限的事件内存在无限次触发，即任意两个连续触发时刻的间隔为0.

定理2 对于多智能体系统(1)，如果设计一个事件触发条件(11)，结合一致性控制(7)，满足系统中任意两个连续触发时刻间隔tk+1-tk都不小于τ，其中

(14)

3 仿真

在这一部分中，基于事件触发的非线性一致性控制协议应用到二阶随机时延系统中，验证所提出理论的有效性.

图1 拓扑图中4个智能体的位置状态Fig.1 Thepositionstatesofthefouragentsinthetopology图2 拓扑图中4个智能体的速度状态Fig.2 Thevelocitystatesofthefouragentsinthetopology

图3 拓扑图中4个智能体触发时刻的值Fig.3 Theevent-triggeredvaluesofthefouragentsinthetopology图4 拓扑图中4个智能体的触发间隔Fig.4 Theevent-triggeredintervalofthefouragentsinthetopology

图5 文献[16]中4个智能体触发时刻的值Fig.5 Theevent-triggeredvaluesoffouragentsin[16]图6 文献[16]中4个智能体的触发间隔Fig.6 Theevent-triggeredintervaloffouragentsin[16]

4 结论

本文研究的是二阶随机时延有限时间一致问题.首先将系统通过函数转化为一般的系统，再结合分布式事件触发条件，提出了一个新的非线性控制输入协议.在异步更新的控制策略下，不仅使得智能体的更新次数减少，而且拓扑中的跟随者可以跟踪到领导者.另外，也证明了所提出的协议和触发条件可以排除芝诺现象.在未来的研究中，可以尝试在高阶系统中研究，还可以针对事件触发的具体条件参数做进一步研究.另外对于系统存在的干扰或不确定性等因素，也将在以后的工作中展开.