24阶群的中心自同构群
张新媛,赵静,宋蔷薇
山西师范大学数学与计算机科学学院,山西 临汾 041000
0 引言
群G到自身的同构称之为群G的自同构.G的全体自同构组成的集合通常用Aut(G)表示.容易证明Aut(G)组成一个群,叫作G的自同构群.设α∈Aut(G),称α为G的中心自同构,如果对任意的g∈G都有g-1gα∈Z(G).G的全体中心自同构组成的集合通常用AutZ(G)(G)表示.容易证明AutZ(G)(G)组成Aut(G)的一个子群,叫作群G的中心自同构群.
许多群论学者都对有限群的中心自同构群进行了研究,并给出很多重要的结论.例如:Adney和Yen研究了有限群的中心自同构群的阶[1].Sanders完全确定了一般p群的中心自同构群的阶[2].Jafari给出了一般有限纯非交换p群的中心自同构群是初等交换群的充要条件[3].后来,Jafari和Jamali又完全确定了非纯的非交换群的中心自同构群的结构[4].本文将给出24阶非交换群的中心自同构群的结构.
1 预备知识
定义1[1]称G是纯非交换群,如果非交换群G没有非平凡的交换的直积因子.显然,对于非交换p群G而言,如果Z(G)循环或者Z(G)≤Φ(G),那么G是纯非交换p群.
定义2[5]设H是有限群,K是有限交换群.记H到K的所有同态构成的集合为Hom(H,K).容易验证Hom(H,K)关于如下定义的乘法运算构成一个交换群:
fg(h)=f(h)g(h)f,g∈Hom(H,K)h∈H
引理1[1]设G是纯非交换群,则|AutZ(G)(G)|=|Hom(G/G′,Z(G))|.
引理2[4]设G=H×K,其中H,K≤G.若H是交换群,K是纯非交换群,则
|AutZ(G)(G)|=|Aut(H)||AutZ(K)(K)||T||U|

引理3[5]设A,C,U是交换群,则
(1)Hom(Cm,Cn)≅Cd,d=gcd(m,n);
(2)Hom(A×C,U)≅Hom(A,C)×Hom(A,U).
引理4[6]设G是有限群,Z(G)≤G′,则AutZ(G)(G)≅Hom(G/G′,Z(G)).
2 主要结果
交换群的中心自同构等于它的自同构群,所以本文我们仅研究24非交换群的中心自同构群的结构.
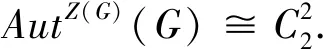
证明 注意到G是极大类群.由文献[7,定理2.5.2]知Z(G)≤G′.从而由引理4可得AutZ(G)(G)≅Hom(G/G′,Z(G)).又因为G是极大类群,所以Z(G)≅C2,G/G′≅C2×C2.根据引理3可知,
Hom(G/G′,Z(G))≅Hom(C2×C2,C2)≅Hom(C2,C2)×Hom(C2,C2)≅C2×C2

定理2 设G是24阶内交换群,则

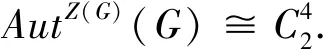
证明 由于G是内交换群,因此由文献[7,定理2.3.7]知G≅M2(2,2),M2(3,1),M2(2,1,1)之一,再由文献[8,引理3.3,3.6]即可得结论.
定理3 设G是24阶非极大类,非内交换的非交换群,则


其中,α1α3=α1,α2α3=α2,α4α3=α4α1,α5α3=α5α2(SmallGroup(32,27)).
证明 (1)当G≅D8*C4时,由于Z(G)循环,因此G是纯非交换群.进而,由引理1可知


(2)令G=H×〈c〉,其中H≅Q8或D8,〈c〉≅C2.不失一般性设
H=〈a,b|a4=1,b2=a2,[a,b]=a2〉≅Q8或H=〈a,b|a4=1,b2=1,[a,b]=a2〉≅D8
首先我们来证明|AutZ(G)(G)|=25.计算知,Z(G)=Z(H)×C2=〈a2〉×〈c〉.因为H′=〈a2〉,所以H/H′≅C2×C2.
1)传感器类设计。图2是传感器类的逻辑结构,传感器对象依靠传感器号来唯一标识。这些属性都是用户可以通过触摸屏来进行设置的。在数据采集中,系统根据传感器对象的采集节点号和通道来读取MODBUS采集到的数据。读取到数据后,系统根据传感器对象的属性,来对采集到的数据进行处理,将其转换成最终数据。在系统中,传感器属性可以选择为模拟量、状态量、数字量、频率量。其中,模拟量可根据设置最大值、最小值以及输入电压范围进行补偿;数字量及频率量可以通过补偿公式进行补偿。
注意到Z(H)≅C2.进而由引理3可知Hom=(〈c〉,Z(H))≅Hom(C2,C2)≅C2Hom(H/H′,〈c〉)≅Hom(C2×C2,C2)≅C2×C2
令T={σf|f∈Hom(〈c〉,Z(H))},U={σf|f∈Hom(H/H′,〈c〉)},则
|T|=|Hom(〈c〉,Z(H))|=2 |U|=|Hom(H/H′,〈c〉)|=22
进而,由引理2可得
|AutZ(G)(G)|=|Aut(〈c〉)||AutZ(H)(H)||T||U|=25
令
由于
o(aαi)=o(a) (bαi)2=(aαi)2o(cαi)=o(c)
且
[aαi,bαi]=(aαi)2[aαi,cαi]=[bαi,cαi]=1
因此αi∈Aut(G),其中i=1,2,3,4,5.下证αi∈AutZ(G)(G).
任取g∈G,不失一般性可设g=aibjck.此时,计算知
g-1gα1=(aibjck)-1(aibjck)α1=c-kb-ja-ia3ibjck=a2i∈Z(G)
类似地可得,g-1gαi∈Z(G),其中i=2,3,4,5.故αi∈AutZ(G)(G),i=1,2,3,4,5.因此,〈α1,α2,α3,α4,α5〉≤AutZ(G)(G).
下面我们来证明|〈α1,α2,α3,α4,α5〉|=25.
容易知道,o(α1)=o(α2)=o(α3)=o(α4)=o(α5)=2.接下来,由于
aαiαj=aαjαibαiαj=bαjαicαiαj=cαjαi,
其中,i∈{1,2,4},j∈{2,3,4,5} 且i 故|〈α1,α2,α3,α4,α5〉|=25.


