基于实测数据的量子遗传算法反演概率积分参数

汪 涛，彭小强，陈兴达，徐 越，赵祥硕

(1.安徽理工大学 测绘学院,安徽 淮南 232001；2．矿山采动灾害空天地协同监测与预警安徽普通高校重点实验室，安徽 淮南 232001；3．矿区环境与灾害协同监测煤炭行业工程研究中心，安徽 淮南 232001)

开采沉陷预计是在开采地下煤炭资源之前对地下煤炭资源开采时可能对地表和岩层造成的影响范围和程度进行预计，以防止对该区域居民的日常生活造成影响，从而对该区域的环境治理工作带来不必要的麻烦。

开采沉陷预计方法根据不同的地质采矿条件各有不同，最传统也是主要的开采沉陷预计方法就是以基本公式中有概率积分而闻名的概率积分法[1]。概率积分参数解算是采用概率积分法进行开采沉陷预计工作的重要步骤之一，常规使用模矢法对概率积分参数进行解算，但是在现在看来，显然精度已经达不到要求，人们在寻求新的概率积分参数解算方法[2]。而智能算法的提出能够很好地解决这个问题，遗传算法作为智能算法之一，通过其种群进化的思想对概率积分法参数进行反演从而得到最优的解。

但是遗传算法有着易早熟、运行速度慢的缺点，为了解决这些缺点，本文旨在利用量子遗传算法量子比特和量子旋转逻辑门收敛速度快、稳定性强的特性，结合矿区的实测数据在遗传算法获得优良解的收敛速度过慢和稳定性不强的情况下，对概率积分参数反演精度进行研究[3]。

1 概率积分预计模型

概率积分法作为开采沉陷预计的主要方法，其在《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规范》中就有提到[4]。概率积分法的基本模型如式(1)所示，公式变量含义如表1所示。

表1 概率积分法公式变量含义

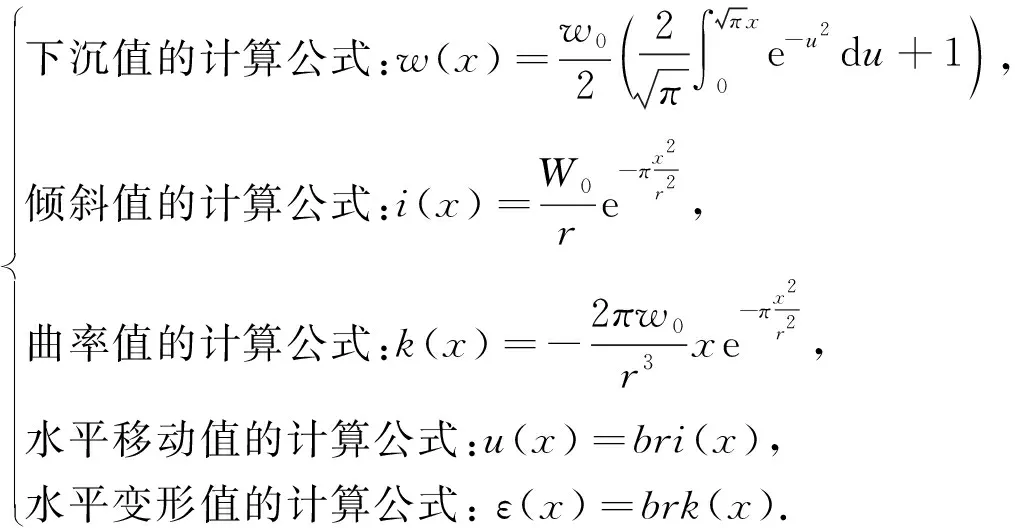
2 遗传算法(SGA)反演概率积分法参数模型

遗传算法是众多智能算法中的一种，它的出现目的是使用自然界优胜劣汰的法则对相关参数进行择优，父代将优秀的基因保留并传递给子代，在这个过程中父代子代的染色体有一定概率根据个体适应度进行选择、交叉、变异行为，最终得出更加优异的子代。

遗传算法简要可以概括为6个部分[5]：

1)种群初始化(通过二进制编码随机得到有一定数量个体的种群)，这部分先随机生成二进制码个体组成种群，最终通过解码得到十进制实数。

式(2)是一个通过将二进制编码转化为十进制实数值(对应区间内)的解码公式。

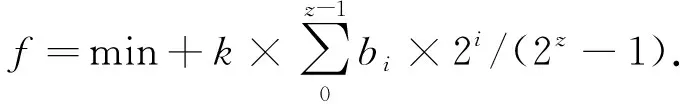
(2)

式中:min是参数的最小值，k是参数的范围长度，z是参数的码长。

2)个体评价(计算个体适应度)，通过适应度函数进行评价然后择优选择后代基因，本文适应度函数依据实测值和算法反演得到的水平移动值、下沉值建立适应度函数，如式(3)所示。

(3)

式中：wp r为算法反演得到的下沉值，up r为算法反演得到的水平移动值，w为实测的下沉值，u为实测的水平移动值。适应度函数值与个体优异性成正比[6]。

3)选择运算(本文使用select函数)。

4)交叉运算(本文使用recombin函数)。

5)变异运算(本文使用mut函数)。

6)终止条件判断。

遗传算法解算过程如图1所示。

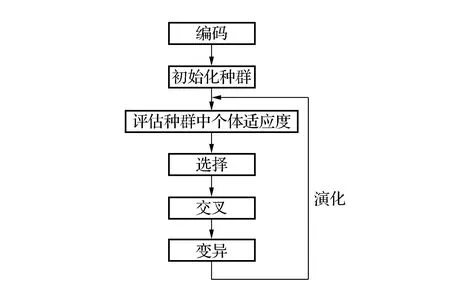
图1 遗传算法过程图解

3 量子遗传算法(QGA)反演概率积分法参数模型

由于SAG算法在选择、交叉、变异环节设置参数不当时易获得局部极值，且SGA算法收敛速度较慢[7]。量子遗传算法利用量子态的纠缠、叠加、干涉的特性对个体进行编码，利用量子逻辑门取代遗传算法中的选择、交叉、变异环节，对染色体个体进行更新操作，能够有效地避免那些缺点，达到更好的效果、更快的收敛速度[8]，因此，本文选择使用量子遗传算法(QGA)对概率积分法参数进行反演。

1)量子遗传算法与遗传算法的不同点主要如下：

①编码方式：使用量子位对解进行编码。

②量子旋转门：不同于SGA的更新操作。

③量子态：由于量子的不确定性，每个量子处于0、1的叠加态(因此QGA的解码方式也就不同)，也正因为如此，量子遗传算法不需要太多的种群数量。

2)量子遗传算法反演概率积分法参数重要步骤：

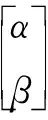
表2 概率积分法公式8个参数

②适应度函数与量子旋转门：本文采用的适应度函数与SGA相同，如式(3)所示，并采用量子旋转门矩阵对种群进行更新，如式(4)所示。

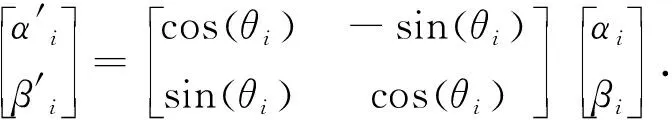
(4)

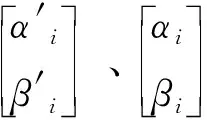
量子遗传算法反演概率积分法流程如图2所示。

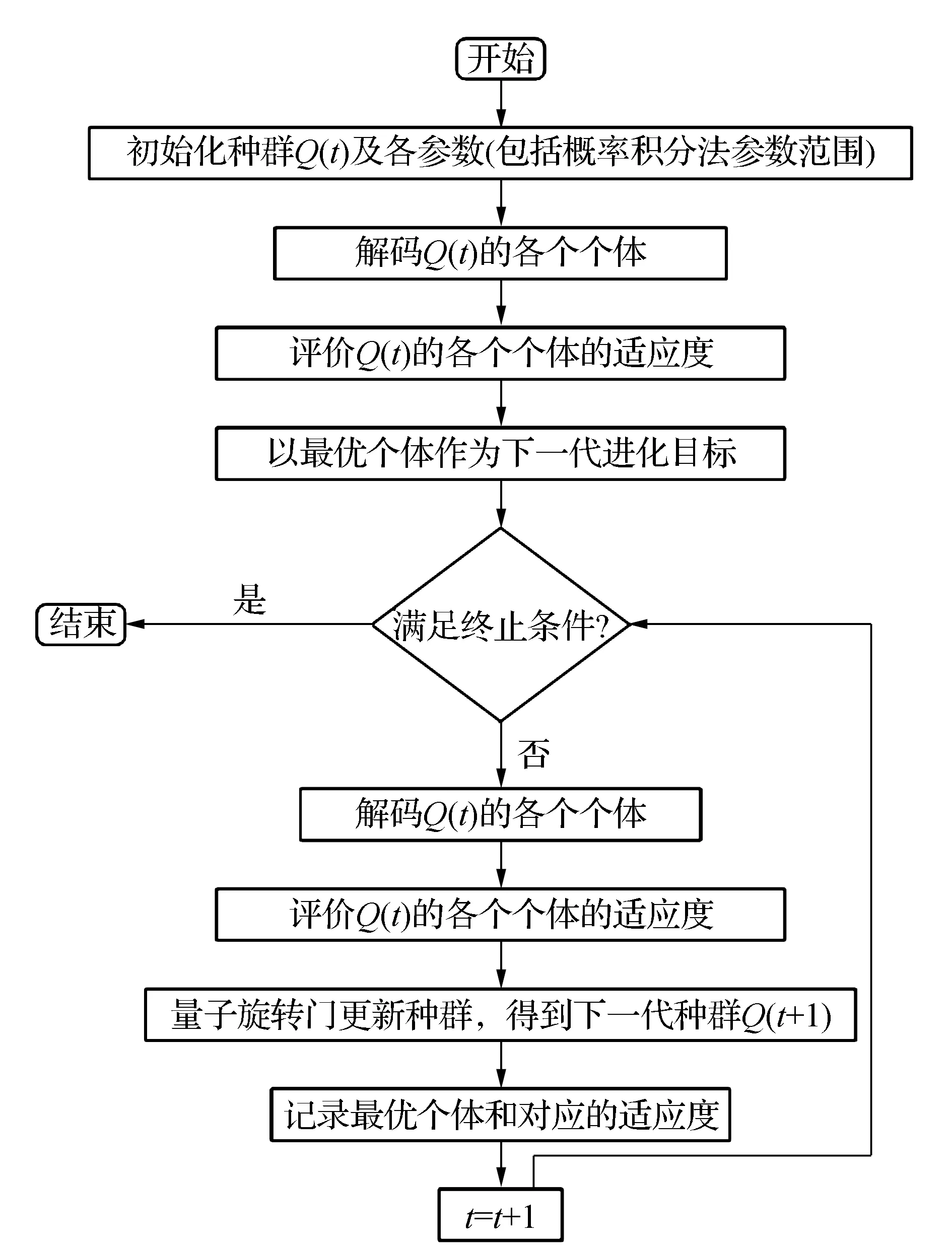
图2 量子遗传算法反演概率积分法流程

4 实例及分析

4.1 观测站概况

淮南某矿区某工作面的地表观测站分布主要有1条长约3.53 km、布设有96个监测点的走向线和半条长约1.5 km、布设有42个监测点的倾向线，每条线上的监测点之间距离在20～40 m之间。从开始的全面观测到最后一次的全面观测中间历时400多天，平均半个月进行一次观测[11]。

工作面及地表监测点分布[12]如图3所示。

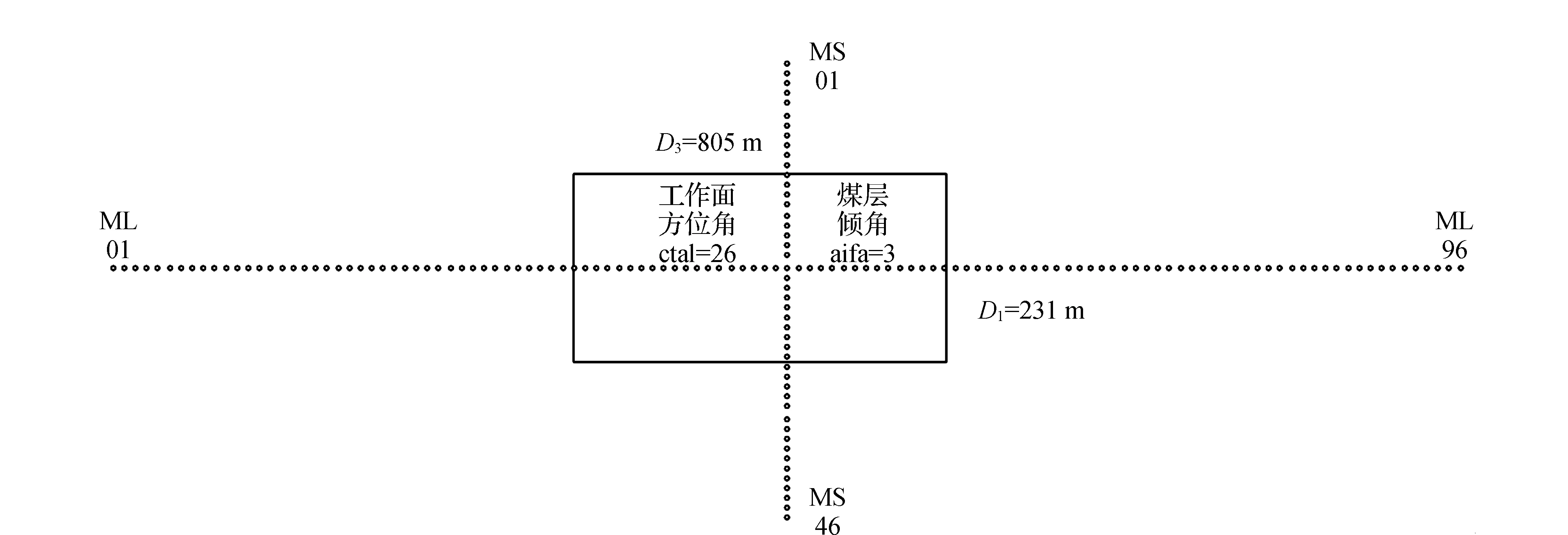
图3 工作面及地表监测点分布

4.2 量子遗传算法反演概率积分法预计参数

本文仅对于走向线上的点的最大下沉值、水平移动值进行讨论，倾向线上的同理可得。

1)遗传算法相关参数及其求取的概率积分法参数。设定个体数100、最大遗传代数100、变量维数8、二进制码长度20、代沟0.9、交叉概率0.4、变异概率0.001。计算的平均时间为69.081 6 s(取10次平均值)。

2) 量子遗传算法相关参数及其求取的概率积分法参数。由于量子态的缘故，所有选取的种群个体数sizepop为20、最大遗传代数MAXGEN为100、各变量的二进制码长度lenchrom=[20 20 20 20 20 20 20 20]。计算的平均时间为3.563 2 s(取10次平均值)。

模矢法求取的概率积分法参数通过资料[12]可得，将模矢法、遗传算法、量子遗传算法求取的概率积分法参数参演值[12]记入表3。

表3 模矢法、遗传算法、量子遗传算法概率积分法参数反演值

3)模矢法、遗传算法、量子遗传算法的精度比较。将模矢法、遗传算法、量子遗传算法得到的概率积分法参数输入程序中得到下沉曲线和水平移动曲线，并与实测数据进行对比，如图4、图5所示。

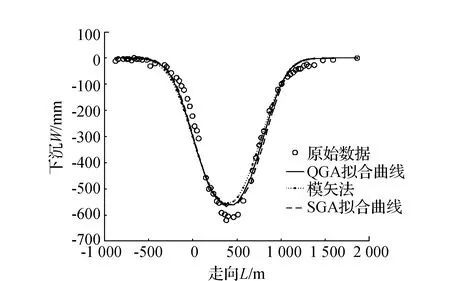
图4 下沉曲线

从图4、图5可以看出量子遗传算法所获得的数据在整体上更加接近于实测数据。

图5 水平移动曲线

通过中误差公式计算相关算法得到点位的下沉值与实测数据的点位下沉值的中误差和均方根误差分别记为Δt、RMSEt，得到点位的水平移动值与实测数据的点位水平移动值的中误差和均方根误差分别记为Δp、RMSEp。它们之间的关系如表4所示(Δt、Δp、RMSEt、RMSEp值越低,精度越高)。

表4 精度比较 mm

从表中可以看出，就点位的下沉值与实测数据的点位下沉值的中误差、均方根误差而言，量子遗传算法的误差精度比遗传算法的误差精度提高了1.8%、1.2%，比模矢法的误差精度提高了12.6%、11.8%。

就点位的下沉值与实测数据的点位下沉值的中误差、均方根误差而言，量子遗传算法的误差精度比遗传算法的误差精度提高了6.2%、6.3%，比模矢法的误差精度提高了12.1%、12.0%。

综上所述，利用量子遗传算法反演的概率积分法预计的最大下沉值和水平移动值的整体精度高，迭代时间短，能够更快地获得最优解(计算的平均时间为3.563 2 s)。

5 结 论

本文通过利用模矢法、遗传算法、量子遗传算法对概率积分法参数反演得到的结果进行分析，可以得出如下结论：

1)量子遗传算法的量子位和量子叠加态给其带来丰富的种群多样性，使其每个染色体可带有多重状态的信息，能够给较少的个体迭代出所需的最优解提供一定的基础，减少了参数反演工作的复杂性和工作量。

2)量子遗传算法使用旋转门操作替代遗传算法中的选择、变异、交叉操作，减少了一定的操作时间，在迭代的过程中每个量子位的状态会逐渐趋于一个状态而达到稳定收敛，从而获得最优解。在一定程度上说明该算法具有良好的收敛精度，有利于解的稳定性。

3)开采沉陷预计常用到概率积分法，概率积分法的参数至关重要，本文只需提前设定好概率积分法参数范围，获得相对准确稳定的参数，可以提高开采沉陷预计的工作效率。