智慧出自直观,洞悉力求无遗
李梦蝶


【摘要】几何直观主要是指利用图形描述和分析问题。借助几何直观可以把复杂的数学问题变得简明、形象,有助于探索解决问题的思路,预测结果。有人说,平面图形和立体图形本身就很直观了,学习和研究空间与图形,还有几何直观什么事呢?那么几何直观在《观察物体(三)》单元中,对培养空间观念能起到什么作用?同时,在本单元学习中,在帮助学生形成空间观念的同时,对学生初步几何直观能力培养又产生什么样的影响?笔者尝试分享几何直观在《观察物体(三)》单元教学中的应用及培养,以求抛砖引玉。
【关键词】空间观念;几何直观;观察物体
发展学生的空间观念是小学空间与图形学习的核心目标。人教版五年级下册数学第一单元《观察物体(三)》以观察物体为载体,让学生从一个或多个方向观察到的图形拼搭出相应的几何组合体,即根据平面图形还原立体图形,包括从给出的一个到三个方向观察到的图形拼搭出相应的几何组合体。或者根据给出的立体图形,画出三视图(正面视图、左面视图和前面视图)。通过大量操作,引导学生逐渐发现实物与他们观察到的图形之间的联系,不断地发展学生的空间观念。而在此过程中,几何直观功不可没。反过来说,在发展空间观念的同时,促进了几何直观能力的培养。
教材是根据学生已有经验及心理发展规律,从一维视图、二维视图到三维视图,螺旋上升,帮助学生建立表象,训练空间想象能力。下面依次赏析几何直观在其中的作用及其生长。
一、横岭侧峰,各司其境
借助几何直观,看图想事,看图说理,帮助刻画和描述问题,使问题变得直观、简单。例如:
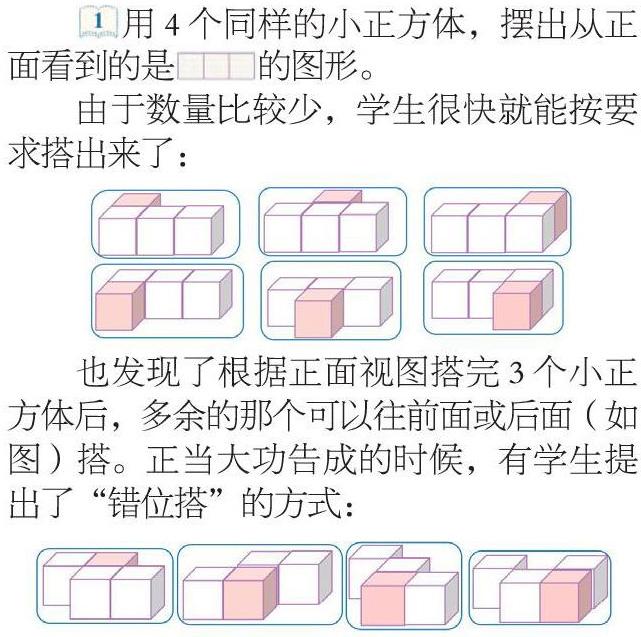
用4个同样的小正方体,摆出从正面看到的是的图形。
由于数量比较少,学生很快就能按要求搭出来了:
也发现了根据正面视图搭完3个小正方体后,多余的那个可以往前面或后面(如图)搭。正当大功告成的时候,有学生提出了“错位搭”的方式:
动手操作帮助学生从直观观察立体图形,头脑中建立表象,能够根据直观立体图形进行想象。本单元所有要摆的立体图形都是组合的小正方体,它们中间是没有分开的,不涉及错开情形。但学生已经摆出来了。怎么处理呢?
这是难得的课堂生成的资源。何不借此来思考“正面视图是怎么得来的?它限定了立体长宽高的哪一个维度?”
通过改变例题:
用4个同样的小正方体,摆出从左面看到的是的图形。
用4个同样的小正方体,摆出从上面看到的是的图形。
在不断的操作中,引发了学生对操作背后的思考,也明白了每一面视图都提供了不同的信息:
只给出小方块的总数和某一方向的视图,搭小方块的方法。
正如苏轼的“横看成岭侧成峰,远近高低各不同”,不同方向的视图,给我们的信息也不一样,明白各自的功能,建立的几何直观图表进行空间想象,通过逆向推理,根据观察到的形状图还原出不同的立体图形。学生图表结合,促进了几何直观能力的养成。
二、析微察异,洞中肯綮
借助几何直观,帮助发现、寻找解决问题的思路。在一维视图中,学生知道了每一方向视图的作用。如果给出了二维的视图,又怎样发现解决问题的关键呢?例如:
还可以有其他的搭放情况吗?没有了。只能用5个小正方体搭放。
又如:小明搭了一个立体图形,从上面看到的形状是图①,从正面看到的形状是图②。搭一个这样的立体图形,小明最少需要( )个小正方体,最多需要( )个小正方体。
为什么都是给出“上面视图”和“正面视图”,为什么第一个问题只有一种摆法,而第二个问题有“至多”和“至少”两种情况呢?通过观察、思考,学生知道了“当前后左右遮挡的位置不是唯一时,会出现至多或至少的情况。”
在对比操作中,根据给定的两个方向观察到的平面视图,确定搭成这个立体图形所需要的立方体的数量范围,让学生认识到根据从两个方向看到的图形,有时不能唯一确定一个物体。学生联想与推理相结合,促进了几何直观能力的养成。
三、仰观俯察,全局于心
给出一面、两面视图时,有时搭放的立体不是唯一的,如果给出三面视图,考虑的情况就更多了。画立体图对于小学五、六年级的学生来说,是挺困难的。用什么来解决这个问题呢?借助几何直观,探索解决三视图、俯视叠加图和立体图形之间关系的思路,预测结果。又如:
从“前面视图”和“左面视图”的交叉重叠部分,我们知道“第2列后行的位置摆了2个小正方体。”
从“立体—三视图—立体—俯视叠加图—三视图/立体”,学生们在大量的互逆操作、观察、思考中積累经验,培养几何直观能力。再如:
搭的这组积木,从正面看是 ① ,从左面看是 ③ 。
奥苏贝尔认为“有意义学习过程的实质,就是符号所代表的新知识与学习者认知结构中已有的适当观念建立非人为的和实质性的联系。”学生从俯视叠加图可以看出,正面视图应为“3列3层”,左面视图应为“2行3层,后行是3层,前行是2层”。学生通过摆来验证自己的推理。学生符号语言与图形语言相结合,促进了几何直观能力的养成!
从一维、二维到三维空间的转化,学生在想一想,画一画,摆一摆,填一填等操作中,伴随观察、猜想、分析、推理、交流、创造等一系列的数学活动中,发展空间观念、推理能力、抽象能力、几何直观能力。
[本文系2013年广东省教育科学“十二五”规划项目(强师工程)的教育科研一般项目课题“初步几何直观意识在小学数学中的渗透与培养研究”(课题编号:2013YQJK056)阶段性研究成果]
参考文献:
[1]邸莉.浅谈在小学数学教学中将发展空间观念落在实处[J].中国电力教育,2008(10):89-90
[2]孔凡哲,史亮.几何课程设计方式的比较分析——直观几何、实验几何与综合几何课程设计的国际比较[J].数学通报,2006,45(10).

