Majorana束缚态对正常金属/三量子点/超导结构输运性质的影响

秦芳，孙艳秀，王素新

(河北民族师范学院 物理与电子工程系，河北 承德 067000)

拓扑超导体中的Majorana束缚态(MBSs)[1]遵从非阿贝尔统计，在拓扑量子计算领域有很大应用前景.

2008年，Fu和Kane[2-3]在理论上提出利用s波超导体和强拓扑超导体界面处的诱导效应，在拓扑绝缘体和s波超导体的界面上可以出现MBSs.这意味着MBSs可以在固体中实现，其应用也变得更为可行.然而，怎样检测与验证MBSs的存在仍然是一个复杂而难以解决的问题.量子点作为一种具有许多新奇量子效应的量子结构，因为结构简单、现象独特而明显，成为一种比较有希望用来检测MBSs存在的装置.科学家们尝试了多种量子点与MBSs的组合构造方式[4-6]，其中，将量子点嵌入超导电极和普通电极之间的结构，由于会产生Andreev反射而引起了广泛关注[7-10].

正常反射一般是入射一个电子，反射回一个电子.当电子由正常金属入射到金属-超导界面时，如果电子能量小于超导能隙，会与一个与之自旋方向相反的电子形成库珀对隧穿到超导体中，同时向正常金属反射回一个与入射电子的速度大小相等、方向相反的空穴.这种电子与空穴的转换就是Andreev反射.近年来，超导体与介观系统耦合的体系由于能够产生Andreev反射现象，引起了广泛关注，尤其是耦合MBSs的量子点体系.例如Law等[7]研究发现，MBSs会引起导线到超导体的共振Andreev反射.Liu等[9]研究了正常金属/量子点/拓扑超导体/量子点/正常金属体系输运性质，研究表明MBSs在拓扑超导体中的非局域特性会导致交叉Andreev反射和电子透射的产生．从当前一些公布的实验结果中不难发现，将MBSs连接到量子点体系之后，原有量子点系统的输运性质会发生改变，产生出一些新奇的特点.这些研究成果为探测MBSs的存在提供了行之有效的方案.

本文提出了耦合MBSs线型三量子点结构模型，并将正常金属和超导电极与中间量子点相连，利用非平衡格林函数方法研究了该体系的Andreev反射性质，重点讨论了MBSs、量子点能级以及量子点与电极之间的耦合强度的变化对体系Andreev反射的影响，并对数值模拟结果进行了较为细致的分析．

1 模型

耦合MBSs线型三量子点体系结构如图1所示，量子点QD1左端连接正常金属电极N，右端与超导电极S相连，QD1上方耦合量子点QD2，下方耦合量子点QD3，QD3下方有一个具有极强Rashba自旋轨道耦合的一维半导体纳米线，将纳米线置于s波超导体表面，且沿纳米线方向施加一均匀外磁场，由于近邻效应和强磁场的作用，纳米线两端将会出现2个局域的MBSs[11]，分别以η1和η2标记，其中η1与QD3耦合．该体系的哈密顿可以写作

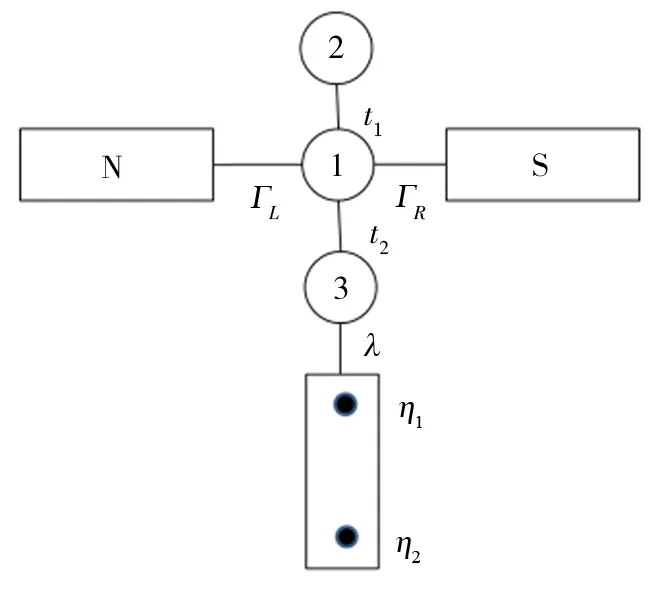
图1 连接在正常金属电极N和超导电极S两端的耦合MBSs线型三量子点结构示意Fig.1 Sketch of a linetype triple quantum dots system with side-coupled MBSs between N and S leads

H=HLeads+Hdots+HT+HM，

(1)

其中

(2)

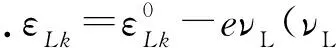
(3)

由于电流守恒，从左电极到中心散射区域的电流可通过左电极粒子数算符对时间微分来计算[12]

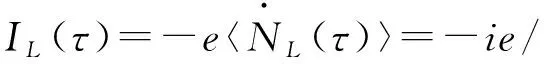
(4)

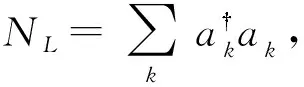
(5)

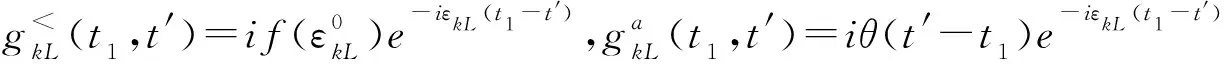
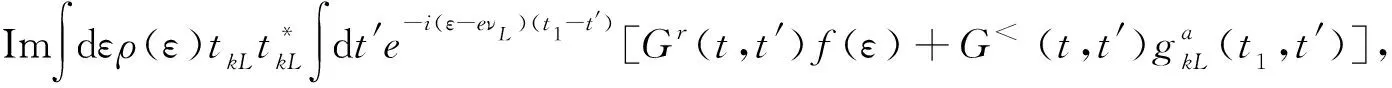
(6)

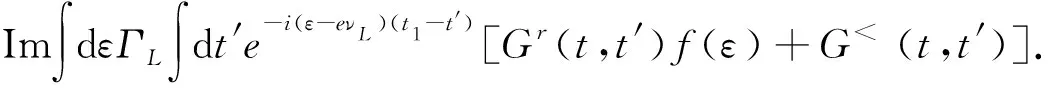
(7)

利用非平衡格林函数及Dyson运动方程，得[13]

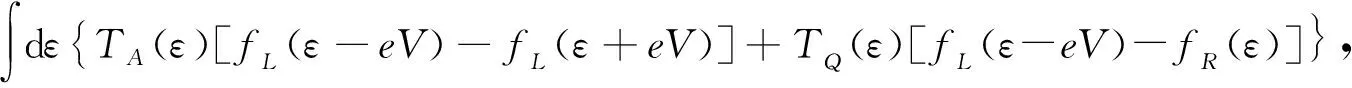
(8)

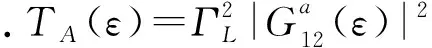
(9)

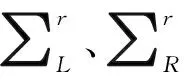
(10)

式(10)中ρR(ε)是修正的Bardeen-Cooper-Schrieffer态密度，表示为[15]

(11)

最后，一旦求得Andreev反射概率，就可以根据Landuer-Büttiker公式计算Andreev反射电导[16]

(12)

2 结果与讨论

首先研究2个MBSs之间的耦合能为零时三量子点体系Andreev反射电导随费米能的变化．计算结果如图2所示．

计算过程仅考虑ε2=-ε3=ε0，t1=t2=t的对称情况，取Δ作为能量单位，设ε1=0，ΓL=ΓR=Γ=0.15．图2a-c分别对应ε0=0，0.05和0.1．实线表示体系未耦合MBSs的情况；虚线表示体系与MBSs耦合且λ=0.06的结果．

首先，从图2a中实线可以发现，ε0=0时，零费米能处Andreev反射电导为0，两侧对称分布2个共振峰，峰值G0=2e2/h；ε0≠0时，如图2b-c中的实线所示，零费米能处出现电导峰，峰值与两侧共振峰相等，峰宽随ε0增大变宽，但两侧共振峰宽度却随ε0增大而变窄，且峰值位置向左右两侧移动．由于三量子点体系的本征态随ε0的增大而增大，导致量子点在各自位置上的局域化程度越来越强，因而出现上述现象.由于QD2、QD3没有与电极直接耦合，所以两侧电导峰越来越窄，而由于中心零能级局域在QD1，因此零点电导峰变宽．ε0=0时零能电导峰的消失可以用类分子态与两端电极的解耦来解释[17]．观察图2中λ=0.06的曲线还可看到，耦合MBSs后零点电导峰两侧出现了一对新的共振峰，且当ε0≠0时又有一对新的共振峰出现．这是由于体系耦合MBSs后增加了新的输运通道，原有的干涉条件发生了变化所导致的．进而将图2b、图2c中的实线与虚线进行对比，可以明显看到当ε0≠0时，体系耦合MBSs后，零点电导峰降为原来的一半，即为0.5G0．

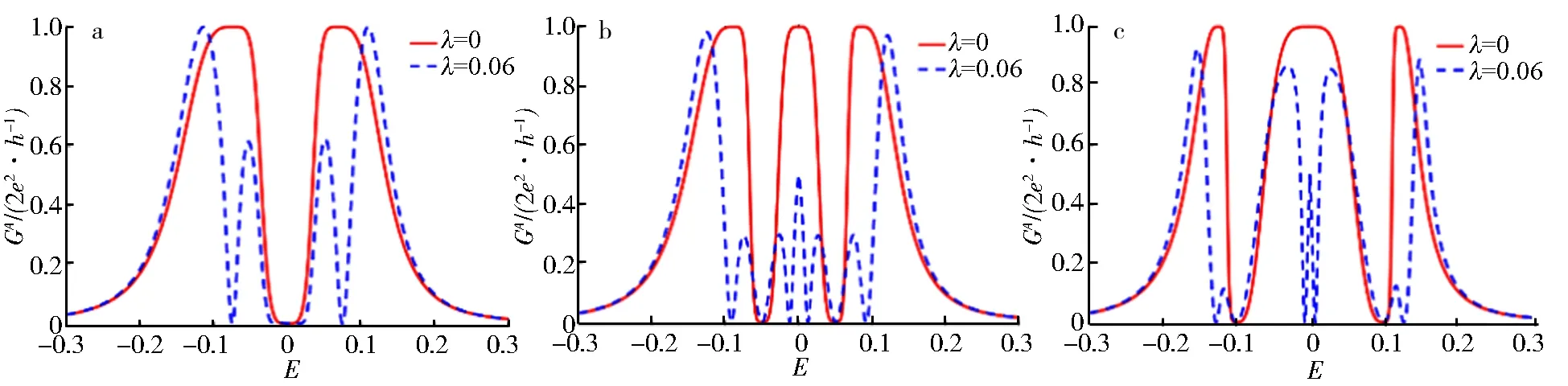
a.ε0=0; b.ε0=0.05; c.ε0=0.1.

为了进一步研究这个半整数的零点电导峰的性质，计算了未考虑MBSs间耦合能时，耦合MBSs三量子点体系Andreev反射电导与ε0、λ、Γ、t的关系．结果如图3所示．

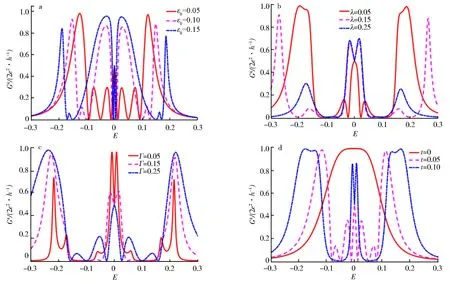
a.量子点能级改变；b.量子点与MBSs间耦合能改变；c.量子点与电极间耦合能改变；d.量子点间耦合能改变.

图3a-d分别表示量子点能级ε0、量子点与MBSs间的耦合能λ、量子点与电极间的耦合强度Γ以及量子点之间的耦合能t对Andreev反射电导的影响．由图3a可见，量子点能级ε0增大使费米能零点两侧振荡峰变宽，峰值变大．图3b、3d表明，随着量子点与MBSs间或QD1与QD2、QD1与QD3间耦合强度的增大，零费米能两侧的电导逐渐增强，导致在GA-E曲线图中零点费米能处曲线由原来的峰变成了谷．而图3c所呈现的变化趋势恰好与之相反，随着QD1与两电极耦合强度的增强，零点费米能附近的曲线由谷变成了峰．可见ε0、λ、Γ、t对零点能之外的共振峰的宽度、高度、数目等均有影响．但值得关注的是以上4个子图中的3条曲线零费米能处电导峰全部固定在0.5G0不变，不随ε、λ、Γ、t的变化而改变，该情况明显不同于量子点耦合普通费米子零能模(G=0)[18]或耦合玻色子的情况[19]．该零点0.5G0电导峰是体系耦合MBSs的明显标志．

如果半导体纳米线的长度可与超导相干长度ξ相比拟，此时纳米线两端的MBSs将彼此相耦合，εM不再等于零．图4是考虑MBSs间的耦合后，Andreev反射电导曲线随着各参数的变化所呈现的不同情况．

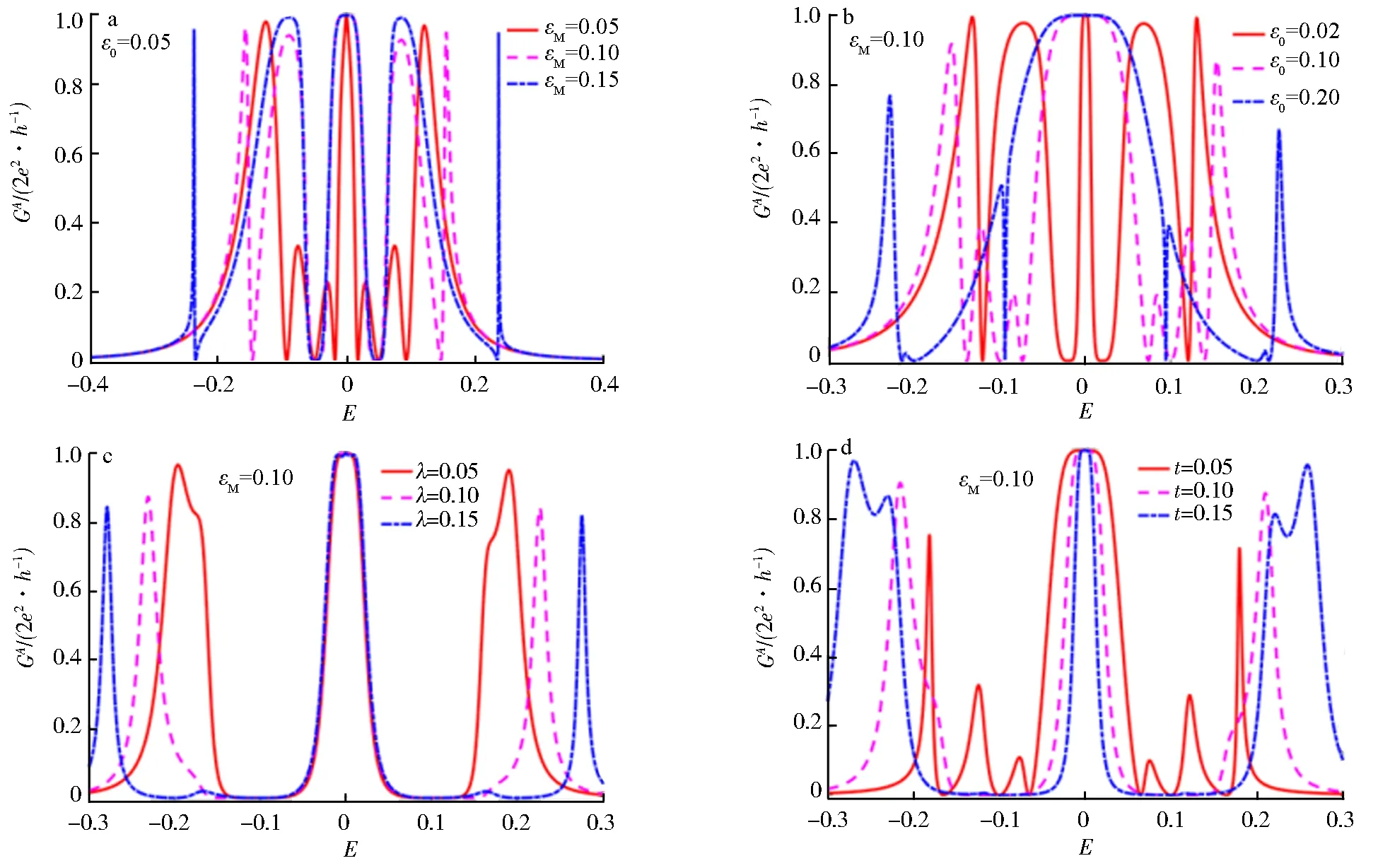
a.MBSs间耦合能改变；b.量子点能级改变；c.量子点与MBSs间耦合能改变；d.量子点间耦合能改变.

观察图4a-d，相比于εM=0的情况，可以清晰地看到εM使零费米能处的电导值从0.5G0增加到未耦合MBSs时的电导值G0，而且无论各参数ε0、λ、εM、t、Γ(文中未呈现)如何变化，零费米能处的电导值始终固定在G0不发生任何变化．由图4a还可以发现随着εM的增大，零点电导峰两侧的所有振荡峰均对称地向左右两侧移动．比较图2b与图4a，MBSs间的耦合能虽然使零点费米能处的电导值与未耦合MBSs的三量子点体系的电导值相同，但体系的Andreev反射电导曲线仍然明显不同于未耦合MBSs时的情况．

3 结论

提出了耦合MBSs的正常金属/线型三量子点/超导结构模型，利用非平衡格林函数方法推导出该体系在零温情况下的电流公式，研究了Andreev反射电导随费米能的变化规律．研究表明，连接在正常金属和超导电极之间的三量子点体系在耦合MBSs后，其GA-E曲线在零费米能两侧振荡峰的数目、宽度、量值发生了明显变化．尤其是未考虑MBSs间的耦合时，零费米能处的Andreev反射电导值始终等于0.5G0(G0=2e2/h)，该量值不随ε0、λ、Γ、t的变化而改变，充分体现了MBSs的鲁棒性．对比耦合MBSs单量子点体系和双量子点体系，三量子点体系的Andreev反射电导曲线呈现出更丰富的物理内容，具有更高的研究价值及广阔的应用前景．