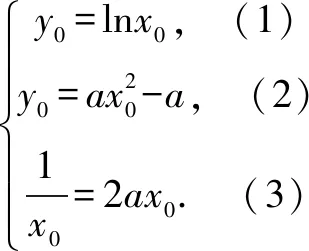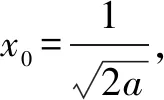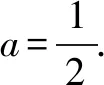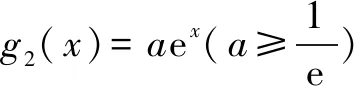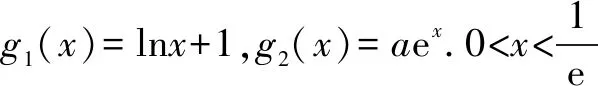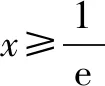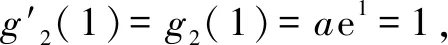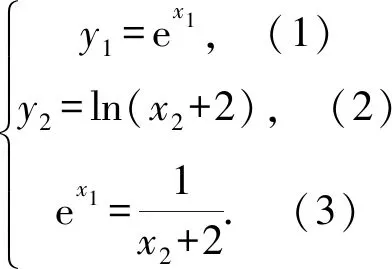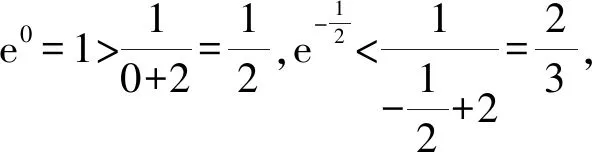借助切线解决函数不等式恒成立问题

李 伟

(辽宁省鞍山市第三中学 114000)

对于函数y=ax2+bx+c(a>0)、y=ax(01)、y=sinx,x∈(0，π)等函数具有以下特征：对于曲线上任意一点处的切线总在该曲线的上方.此直观结果虽然简单明了，但用其解决函数不等式恒成立等问题时能起到直观易懂、事倍功半的效果.下面以三道高考试题作为示例，说明如下.

示例1 (2017年理科全国二卷21题)已知函数f(x)=ax3-ax-xlnx,且f(x)≥0.

(1)求a；

(2)证明：f(x)存在唯一的极大值点x0，且e-2

分析问题(1)，注意到函数定义域为x>0，所以f(x)≥0等价于以ax2-a-lnx≥0，即ax2-a≥lnx.构造函数g1(x)=lnx,g2(x)=ax2-a.a≤0时，由函数g1(x)与g2(x)图象知，此时不合题意.a>0时，注意到g1(x)=lnx任意一点的切线都在曲线上方，g2(x)=ax2-a任意一点的切线都在曲线下方；所以如果函数g1(x)=lnx、g2(x)=ax2-a的图象存在共点公切线，则其公切线所确定的a即为所求.

问题(2)证明略.

反思解题关键在于由lnx≤ax2-a，构造两个函数g1(x)=lnx，g2(x)=ax2-a，借助g1(x)=lnx，g2(x)=ax2-a存在过两曲线公共点的公切线，并且两个函数图象分别在公切线的上、下方，这样就得到取等号时a的值.

示例2 (2018年理科全国一卷21题)已知函数f(x)=aex-lnx-1.

(1)设x=2是f(x)的极值点，求a，并求f(x)的单调区间；

分析问题(1)略.

略解问题(1)答案：递减区间(0,2)；递增区间(2，+∞).

反思与示例1比较，示例2是求参数范围的问题.该题解法与示例1的区别在于先求出参数的临界值(即取等号的参数值)，再思考参数的考取值范围.

示例3 (2013年理科全国二卷21题)已知函数f(x)=ex-ln(x+m).

(1)设x=0是f(x)的极值点，求m，并讨论f(x)的单调性；

(2)当m≤2时，证明f(x)>0.

分析问题(1)略.

对于问题(2)，f(x)>0即ex>ln(x+m).由于m≤2，由对数函数单调性得：ln(x+2)≥ln(x+m)，因此，只需证ex>ln(x+2)①即可.

构造函数g1(x)=ex、g2(x)=ln(x+2).注意到g2(x)=ln(x+2)切线在其曲线上方，g1(x)=ex切线在其曲线下方.由于本题的不等式是大于号，不可能存在共点公切线，所以不能简单运用上述示例的方法解决.通过进一步的思考可得，如果存在互相平行的切线，也可得①式成立.

由(3)得-x1=ln(x2+2)，

y1-y2=ex1-ln(x2+2)=ex1+x1②.

反思与示例1、2比较而言，示例3中函数不等式的符号是“>”，所以不存在共点的公切线.因此借助平行切线的方法来解决.其它解题过程与示例2的求解思考相同.

事实上，还有很多用此方法可以解决的数学问题(如包含正、余弦函数的问题)，由于上述三种类型基本将其概括，其解题思考也基本雷同，就不过多赘述.

最后，作为这类问题求解的反思，提出以下注记：

一是文章中提出的函数图象特征(图象在其切线上方，或下方)涉及到凸函数的概念.也就是说，凸函数是借助函数图象在其任意一点的切线上、下方来定义的(见参考文献[1]).对于一个函数是否是凸函数的判断方法是：f″(x)>0(<0)是下(上)凸函数.所以判断一个函数是否是下(上)凸函数需要两次求导，判断正负即可.虽然高中没有涉及这些知识，但对学过导数的高中生来讲并不存在学习负担.

二是运用曲线切线的方法解决证明不等式、含参不等式等恒成立问题，其解题思路非常简洁直观、解题思维量很小，特别是对于同时含有两个超越代数式(如：ex、lnx、sinx、cosx等)的函数问题而言，解题即思考的简洁性更加突出.

三是处理导函数问题时，有时需要将超越式转化为代数式，利用此方法，为通过放缩来实现超越式向代数式的转化，提供一种很好的思考.

五是运用曲线切线不仅能解决凸性相反的不等式恒成立问题，也能解决凸性相同的问题，解题的基本思考是一致的，在此请读者自行思考，就不举例说明了.

综上所述，借助凸函数与切线关系解题不仅限于上述三个示例，也不仅限于上述问题，如解决零点问题，同样是有效的.总之，这种解题思考有较大的开发前景，欢迎感兴趣的同仁们去探索.