几道2020年导数试题的新解法

刘士香 刘才华

(1.山东省泰安市宁阳第一小学 271400；2.山东省泰安市宁阳第一中学 271400)

例1(2020全国卷1文科20题)已知函数f(x)=ex-a(x+2).

(1)当a=1时，讨论f(x)的单调性；

(2)若f(x)有两个零点，求a的取值范围.

解(1)f(x)在(-,0)上单调递减，在(0,+)上单调递增(过程从略).

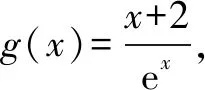
当x∈(-,-1)时，g′(x)>0，g(x)单调递增；当x∈(-1,+)时，g(x)单调递减，于是gmax(x)=g(-1)=e.又从而f(x)有两个零点的充要条件为则的取值范围为).

例2(2020年全国卷1理科21题)已知函数f(x)=ex+ax2-x.

(1)当a=1时，讨论f(x)的单调性；

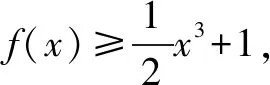
解(1)f(x)在(-,0)上单调递减，在(0,+)上单调递增(过程从略).

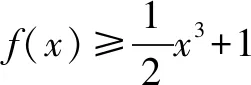
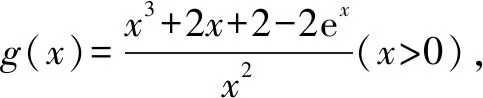
设h(x)=x2+2x+2-2ex(x>0)，则h′(x)=2(x+1-ex).由熟悉的不等式ex≥x+1得h′(x)<0，所以h(x)在(0,+)上单调递减，则h(x)0，g(x)单调递增；当x∈(2,+)时，g′(x)<0，g(x)单调递减，从而

例3(2020年全国2卷理科21题)已知函数f(x)=sin2xsin2x.

(1)讨论f(x)在区间(0,π)的单调性；

解(1)由f(x)=sin2xsin2x=2sin3xcosx得

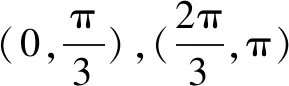
解法2由f(x)=sin2xsin2x=2sin3xcosx

得|f(x)|=2|sinx||sinx||sinx||cosx|.

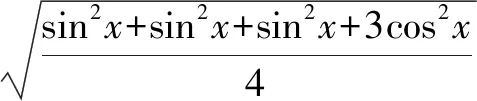
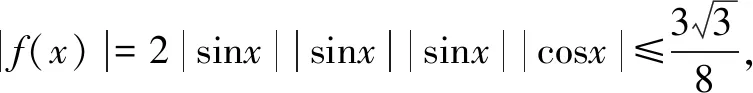
将上述n个式子相乘得

由|sinxsin22nx|≤1得

|sin3xsin32xsin34xsin32n-1xsin32nx|

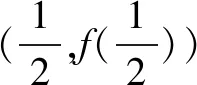
(1)求b；

(2)若f(x)有一个绝对值不大于1的零点，证明：f(x)所有零点的绝对值都不大于1.

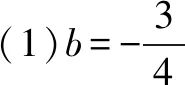
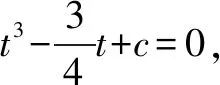
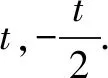
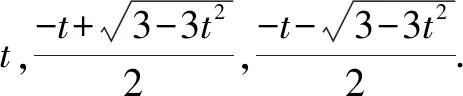
综上，结论得证.

例5(2020年高考山东卷第21题)已知函数f(x)=aex-1-lnx+lna.

(1)当a=e时，求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积；

(2)若f(x)≥1，求a的取值范围.

(2)由题意知x>0且a>0.

当a≥1时，设F(a)=aex-1-lnx+lna，则F(a)在a∈[1,+)上单调递增，则由熟悉的不等式ex≥x+1和lnx≤x-1得F(a)≥F(1)=ex-1-lnx≥x-lnx≥1，即当a≥1时，有f(x)≥1；

当0

综上知a的取值范围为a≥1.