极限思维法在高中物理教学解题中的应用分析

夏光辉

(江苏省丰县中学 221700)

物理是一门开发学生思维的课程，解题的思想方法是非常重要的.物理习题中包含着很多物理问题，学生在解题的过程中应该反映出自己的思维过程，并灵活运用物理知识.当然，学生可以运用的解题方法有很多，极限思维法、建模法都是不错的解决方法.

教师讲授物理知识要充分考量学生已有的知识点，学生学习的知识能够推动高中物理课程的实施.无论是教师还是学生，都应该重视极限学习法对学生学习的帮助，让它成为学生学习的工具.

极限思维法是指在物理问题中，其中一个变量的取值与极限相近，可以将这个变量取固定值，可以是无穷大，也可以是无穷小，当因变量与固定值相近时，这个固定值就成为了极限值.极限法在高中物理解题中比较灵巧，不仅能够帮助学生节省做题的时间，还能保证正确率.但是极限思维法也有自己的适用范围，学生对题目理解不充分，就很可能误用极限思维法.

我们根据数据与处理一节表述的数据，采用第一个被触发台站周围的平坦先验和每个质点滤波定义1 000个质点，进行了质点滤波参数估计近似。这个方法以1s的时间间隔进行更新，而且所有的实验都在模拟的实时中进行。

一、极限思维法的概念

极限思维法可以应用到很多高中物理题目中，是对抽象的问题直观解决的一种方法，它是将复杂的问题简单化，对题目中的极值进行计算，当然要包括题目中的变量，而且物理量是连续单调进行变化的.极限思维法是对题目中的极值进行分析，是极限性假设，它对解决问题以及科学研究都有价值.对于高中物理中那些比较艰涩难懂的问题，学生可以运用极限思维法进行解决.

二、极限思维法的应用策略

自动扶梯在商场中是代步工具，与行人步行相比，自动扶梯更加便捷.当自动扶梯运行，人不运动时，从一楼到二楼需要运用t1；当自动扶梯不动，人通过步行爬楼梯，从一楼到二楼的时间需要t2.如果在自动楼梯运行时，人从楼梯往上走，需要浪费多少时间呢？

1.3 规范化 规范化主要分为位置规范化、大小规范化和笔画细化处理，位置规范化和大小规范化在纸质文字转化为数字图像时，就已规范化，每个单体文字图像像素为长宽各130像素。对于细化方面，细化是指对于一个给定的模式图像，抽取其“中心骨架”的过程，细化算法可分为非迭代算法和迭代算法，而迭代算法又分为串行算法和并行算法，本文的细化处理是在不破坏原有结构配置和给定笔画连接位置关系的基础上，采取迭代扫描并删减边界像素点来完成。笔画细化方法中经典的有基于标记的并行细化算法〔14〕，改进的有自动矢量化算法〔15〕。细化后的文字消减了很多手写字体的个性化特征，为特征提取创造了有利条件。

3.验证答案结果

极限思维法能够帮助学生提高解题效率，取得良好的解题效果，对答案进行验证时也可以运用极限思维法.没有学生在解题的过程中没有运用极限思维法，那么在检查答案结果的时候就可以运用极限思维法，保证答案的准确性.这样学生就可以及时发现错误的答案，提高解题的正确率.

由题目可以看出，时间是由字母表示的，时间和速度可以是任意值.学生运用极限思维法，考虑当t1和t2都趋于无穷时，是符合解题要求的，这种解题方法就比较简单了.

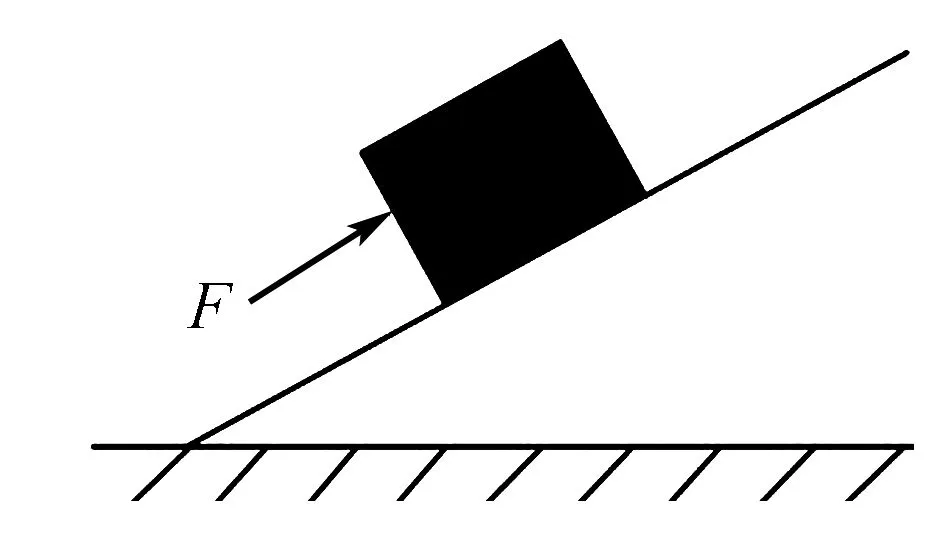
图1

专家共识推荐:NMIBC患者行电切术后应常规行膀胱灌注化疗或免疫治疗，以减少肿瘤复发和进展的几率。即刻灌注则仅能使用化疗药物，并在没有膀胱穿孔或严重出血的前提下，术后尽早完成。

学生在刚面对高中物理题目时，总是不知道该怎样解决，题干中的数量关系也会让学生感到迷惑，在经过思考后也不知道哪个数值是题目的突破口，这时候可以先分析题干中的信息，然后运用极限思维法解决问题.首先，学生在不知所措时，可以先题干中的信息，从题干中总结出已知条件和数量关系，对物理变量进行分析，找到题目中的极限作为解决问题的突破口.

将极限思维法应用到高中物理解题中，要充分考量学生对题目的分析以及对极限思维法的应用情况.当学生解决物理问题时，由于学生的学习能力不同，他们找到的突破口也就会不一样，学生根据自己掌握的极限思维法的应用情况，选择合适的思路解题，提高解题的效率.如果学生更擅长运用其他解题方法，那么学生可以将极限思维法作为解题的协助.在运用极限思维法解决高中物理问题时，要明确极限思维法的解题过程和条件，明确题目中的极限和变量.学生在解决高中物理问题时，不能盲目运用这种方法，要根据题目和运用的知识找到合适的解决思路.在选择题中，学生也可以运用极限思维法，提高解决问题的效率.根据题目我们可以看出：物块M正在F的作用下，处于静止中，斜面作用于M的静摩擦力方向朝哪？在这道题目中，学生就可以运用极限思维法解决问题.首先对F进行假设：第一种情况，当F很大时，物体向上运动，摩擦力沿斜面向下；第二种情况，当F很小时，物体有下滑的趋向，这时摩擦力沿斜面向上；第三种情况，F合适时，物体不运动，这时摩擦力为零；第四种情况，摩擦力大小等于F.

2.提高解题效率

三、极限思维法的应用案例

1.找到解题突破口

这道题的普通解决方法是计算上楼的平均速度，将速度加起来，总速度就是扶梯与人同时运行的速度.

目前，我国在建和正在设计的水利水电枢纽工程多地处西部偏远山区，坝址地形地质条件背景复杂，坝基覆盖层多较为深厚；设计方案经工程造价、建材和施工等要素比选后，选择修建当地材料坝，且以面板堆石坝居多。从耐久性、梯级水库上游库坝的重要性等情况看，高面板坝泄洪建筑物布置和运用安全不如混凝土坝。已运行的面板堆石坝泄水建筑物主要存在以下几方面问题：具有高流速、高泥沙含量的泄水建筑物建设标准不足，泄洪时水力冲刷和雾化导致坝下山体滑坡、交通中断，对输水隧洞工程地质隐患处理不到位，个别工程施工质量不满足要求而导致泄洪建筑物运行期损坏、损毁等。

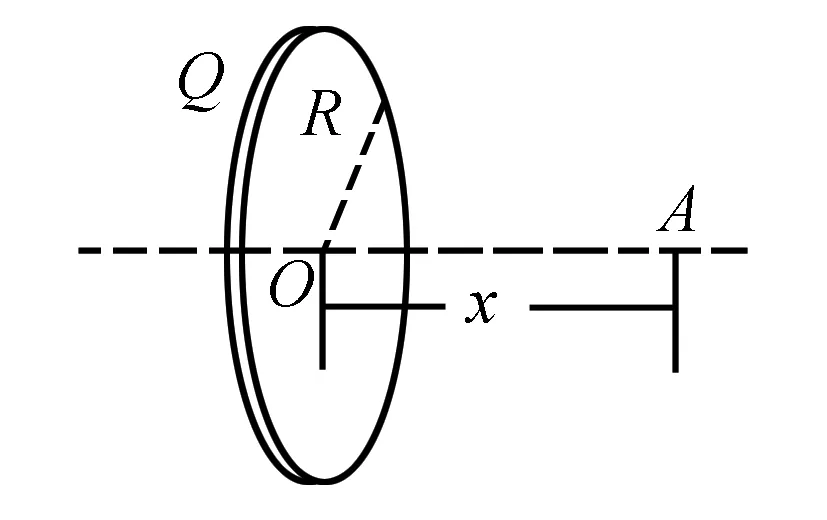
图2

如果t2趋于无穷，也就是人静止不动时，就是人不动、自动楼梯动的时候，那么人动自动楼梯动的时间就和人不动楼梯动的时间差不多了，这时候答案应该与t1接近.当t2趋向于无穷时，答案趋向于t1，当t1趋向于无穷时，答案也是一样的.

除了计算速度方面的问题，极限思维法还可以应用在其他高中物理题目中.比如，在电荷计算的题目中，假设有电荷分布在圆环上，该圆环的半径是r，那么，圆环轴线上离圆心的距离为x的A点的电场强度是多少？

4)选择创建材料对话框，修改材料名称。将密度添加到命名的材料中，修改密度数值。同理可以添加弹性模量等材料参数。

高中生解决这个问题还是有难度的，很难一下就找到问题的突破口，这时候运用极限思维法就可以提高解决问题的效率，解决问题就变得非常简单.在极限思维法中，学生将圆环进行分割，最终得出电荷，由于这个图形是圆环，所以这些电荷就是对称的，这时候再对电场强度进行计算，积累求和，算出最终答案.

总之，学生在面对抽象复杂的问题时，可以运用极限思维法解题.了解极限思维法的解题步骤和应用突破口，通过对题目中的要点进行分析，提高解题效率.文章主要分析了极限思维法应用到物理解题中，让学生找到清晰的学习思路，提升学生的学以致用能力，让学生对知识做到融会贯通.