激光熔覆产生的熔池温度与对流分析

宋博学， 于天彪， 姜兴宇， 郗文超

(东北大学 机械工程与自动化学院， 辽宁 沈阳 110819)

激光熔覆作为一种新兴的增材制造技术[1]，在废旧零件修复[2]、复杂零件成型[3]等领域具有非常大的应用潜力.尽管存在诸多优势，但激光熔覆尚未被大规模使用.除去成本等方面的原因，其根本因素在于熔覆层的成型质量对于工艺参数而言非常敏感,可在基板上形成一个具有高度瞬态性的熔池.在熔覆过程中,熔池内部同时存在大量物理现象[4]，熔池及其周围存在着复杂的热量传递过程，在激光对基板的辐射过程中，一部分热量被金属粉末吸收，另一部分热量被基板吸收，还有一部分热量被金属粉末和基板反射到周围环境中.熔池周围还存在着复杂的质量传递现象:金属粉末在进入熔池前，一部分提前被激光熔化，另一部分在进入熔池后才被熔化.金属粉末进入熔池后经过复杂的质量传输，最终凝固并形成熔覆层.

熔池内部的演变过程对熔覆层成型质量的控制具有重要意义.激光辐射形成的熔池尺寸非常小，且熔池的演变几乎是瞬时性的；因此，通过实验观察等手段对熔池进行实时测量几乎是难以实现的.在这种情况下，对熔池的演变过程进行数值仿真很有必要.目前已有大量关于熔池演变的相关研究:戴德平等[5]通过Abaqus平台模拟了Inconel718在激光熔覆时形成的温度场与应力场，发现径向和周向的残余应力峰值均超过了屈服极限.任仲贺等[6]构建了激光熔覆有限元平台，发现熔覆层的温度具有脉冲式急速上升和呈双曲线形状下降的特征.任朝晖等[7]研究了基于熔丝的激光熔覆的温度场与应力场，认为超声冲击能够缓解残余应力，降低熔覆层开裂的风险.Kumar[8]使用有限体积法求解多块非正交网格系统中的三维传导传热模型，以预测凝固覆层的几何形状和微观结构.

尽管已经有诸多关于激光熔覆的有限元模拟，但鲜有对熔池内部演变及其流动模式的研究.无论是温度还是应力，均取决于热量和质量在熔池内部的传输.熔覆层的成型同样依赖熔池内部的质量传输，因此，构建熔池的演变与传输模型是十分必要的.本文以Kovalev构建的激光辐射在金属基板上的熔池中引起的热毛细微对流模型为基础[9]，引入相关物理模型，构建了激光熔覆熔池的传输模型，揭示了热量和质量在熔池内部的传输模式，并对熔覆层成型的影响进行了探讨.

1 激光熔覆控制方程及其物理模型

1.1 熔池控制方程

激光熔覆原理如图1所示，金属粉末从与基板呈一定角度的喷嘴中喷出，同时激光辐射到金属粉末与基板交汇处.金属粉末和基体同时被激光熔化，最终，进入溶池的粉末凝固并形成熔覆层.与大多数传热传质物理现象相似，激光熔覆形成的熔池在演变过程中遵循着质量守恒、动量守恒以及能量守恒[10].

(1)

(2)

(3)

式中:ρ为密度；t为时间；v为流体速度；ms为质量源项；p为压力；g为重力加速度；T为温度；T0为参考温度；μ为黏度；H为焓；λ为导热系数；hs为与捕获的填充材料液滴相关的焓添加率的源项.此外，本文还考虑了热源及热边界、流体边界、相变及表面张力等物理模型.

1.2 热源及热边界条件

激光热源可以通过高斯分布近似表示:

(4)

式中:q(r)为与激光作用点距离为r的热流密度；Q为激光功率；η为吸收率；r0为激光光斑半径.

通过式(5)所示的守恒条件使热量仅施加于表面单元[11]:

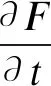
(5)

式中:F为一个网格内的流体体积分数；dF为体积分数对不同网格方向的微分.

1.3 流体边界

在网格边界处，利用网格周围的虚构单元格层设置流体边界.在i=1和i=2的边界处:i=1的网格是直接设置的，而不是计算得到的；而i=2的网格属性可根据有限差分法计算得到，如式(6)所示.并且在边界单元格处，所有的法向速度均为0.

(6)

1.4 表面张力

激光熔池表面温度的变化引起了流体表面张力梯度的变化，并诱发了表面流体从低表面张力区域向高表面张力区域流动.这种Marangoni流动是熔池内质量传输的主要驱动力[12]:

γ=γ0-σ(T-T0).

(7)

式中:γ0为参考温度T0下的表面张力；σ为表面张力系数.

1.5 热物理属性

材料的物理属性在高温下会发生明显变化.本文基于CALPHAD方法对具有特定成分的材料进行了计算[13-14]:

.

(8)

本文构建的模型基于牌号为RCF103的商用合金粉末，其成分如表1所示.将表1中的成分代入式(8)，可获得依赖于温度的热物理属性，如图2所示.其他相关的物理属性如表2所示.

表1 RCF103合金粉末的主要成分(质量分数)

表2 与模型相关的物理属性

2 结果与讨论

2.1 模型验证

通过解守恒方程可以获得在设定时间内的熔覆层形貌，如图3所示.

为了验证获得的熔覆层形貌与实际工艺参数的对应关系，本文还设计了3组激光熔覆实验，所选取的工艺参数如表3所示.三组对比结果如图4所示.

由图4可知，仿真结果与实验结果具有良好的吻合特征，因此本文构建的模型对于研究激光熔覆的熔池演变而言是可靠的.

2.2 熔池的温度场

由于激光的能量密度非常高，造成熔池在极短的时间内形成，因此，在熔池周围会形成具有巨大温度梯度的温度场，如图5所示.

表3 实验参数

图5表明，由于激光能量直接传输到熔池表面，造成熔池表面的温度最高，达到了约3 100 K.从熔池表面延伸至熔池边缘，温度逐渐降低.熔池边缘的厚度即温度场中液相线与固相线之间的距离.尽管熔池尺寸很小，但温度场的分布范围非常广.从熔池边缘延伸至基体的一段距离内，产生的高温不会使基体熔化，但会使基体发生再奥氏体化，结果就是在凝固后的熔池周围产生马氏体相变.

2.3 熔池的对流形式

在温度梯度与表面张力梯度的作用下，熔池内部发生强烈的Marangoni运动.熔池及其周围的流场如图6所示.

图6a表明在垂直于扫描方向上，存在两个对称的环形对流.在粉末到达熔池表面后并不是直接进入熔池底部，而是受表面张力的作用沿着熔池表面流向熔池两侧，并在两个熔池边缘进入熔池底部.在行进过程中一部分凝固，另一部分在Marangoni驱动的作用下重新流向熔池表面.这也说明了驱动流体向熔池表面的Marangoni作用大于驱使流体流向熔池底部的Stokes运动.

图6b清楚地揭示了熔覆层的质量来源主要为从熔池底部流向熔池表面的流体.可知，在平行于扫描方向上，存在着一个几乎包含于整个熔池的逆时针环形对流.与图6a的结果类似，到达熔池表面的粉末进入熔池后，一部分凝固于熔池底部，另一部分在Marangoni驱动的作用下流向熔池后边缘，并在表面张力梯度的作用下流向激光作用点的前方.在熔池表面的流体流向发生转变，而发生流向转变的点即为表面张力梯度为0的点.

尽管Marangoni驱动占据着主要地位，但Stokes运动依然存在，因此相比合金粉末中的Fe，其余较重的元素(例如Mo，Nb)的流动速度较慢.当这类元素的质量分数达到某一临界值后，很容易发生宏观偏析，造成熔覆层的成分分布不均匀.因此，通过分析熔池内部的对流模式，在选择激光熔覆材料时，对于具有相似质量分数的元素的摩尔质量不宜相差过大.

3 结 论

1) 构建了能够揭示激光熔覆熔池温度与对流的数值仿真模型.

2) 熔池内部存在巨大的温度梯度，且从熔池底部延伸至基体的一部分会发生再奥氏体化与马氏体相变.

3) 熔池内部的对流形式主要为环形对流.合金粉末到达熔池后在Marangoni驱动作用的影响下先沿着熔池边缘进入熔池底部，再重新流向熔池表面.

4) 合金粉末中具有相似质量分数的元素如果其摩尔质量相差过大，将会引起宏观偏析，使熔覆层的成分分布不均匀.