Galton-Watson过程中极限鞅密度函数的Lipschitz连续性

侯婉婷， 张美娟

(1. 东北大学 理学院， 辽宁 沈阳 110819; 2. 中央财经大学 统计与数学学院， 北京 100081)

分枝过程是近几十年概率论研究的热点课题，包括Galton-Watson过程、连续时间马氏分枝过程、年龄依赖分枝过程、多物种分枝过程,Dawson-Watanabe超过程及测度值分枝过程等.分枝过程相关问题的研究有深刻的理论意义, 一方面可探讨分枝过程的概率性质[1], 另一方面通过建立分枝机制等方法, 利用分枝过程的性质解决相关的随机游动[2-5]、随机图、随机树[6]等问题. 分枝过程有广泛的应用价值, 在物种繁衍、核子裂变、细胞分裂等现象[7]及传染病学[8]的研究中, 可通过研究分枝过程随机数学模型解决实际问题.近年来，多物种分枝过程[9]、随机环境与变环境中的分枝过程[10]、分枝随机游动与带移民的分枝过程[11]等成为研究的热点问题.

1 拟解决的问题

若EZ1lnZ1<，则对任意的ε>0,ω(x)在[ε,)中是Lipschitz连续的，阶为δ′=min(δ,1).

但是在其证明推导的过程中，需要δ≠1. 也就是说，依其证明，只能得到δ≠1时,ω(x)是Lipschitz连续的，其阶为δ′=min(δ,1).

本文对该定理的证明及结论进行了修正和补充，研究密度函数ω(x)的Lipschitz连续性，得到阶的精细刻画:

定理 1假设m>1,EZ1lnZ1<,q=0，则

1) 若δ≠1，则对任意的ε>0,ω(x)在[ε,)中是Lipschitz连续的，阶为δ′=min(δ,1)[1].也就是说，∀ε>0,存在常数c，使得∀y1,y2∈[ε,),有

|ω(y1)-ω(y2)|≤c|y1-y2|δ′.

(1)

2) 若δ=1，则对任意的ε>0,ω(x)在[ε,)中是Lipschitz连续的，阶为即∀ε>0, 存在常数c，使得∀y1,y2∈[ε,), 有

定理 1 是在Kesten-Stigum定理的基础上，推导出的Galton-Watson过程鞅极限的密度函数的Lipschitz连续性.此外，Seneta-Heyde定理也是关于鞅收敛性质的经典定理.对随机环境中的分枝过程，Tanny[13]研究了相应的Kesten-Stigum定理和Seneta-Heyde定理；Hong等[14]研究了均值无穷情形下鞅的极限性质.

2 式(1)证明的修正[1]

首先叙述文献[1]中的证明, 在证明细节中说明文献[1]中的证明需加以修正的地方.

引理 1 当m>1，EZ1lnZ1<,q=0 时，对实数u,有

sup|u|1+δ|ψ′(u)|<,

对任意的y1,y2>0,有

(2)

由于ψ′可积, 故对第一部分I1存在常数c1,使得

(3)

(4)

当δ≥1时，由文献[1]可知:

(5)

其中c′为常数.

式(5)仅在δ>1时才成立,这是因为在式(4)中，有

由ψ′可积知:

由引理1知:

当δ>1时，结合(4)可知:

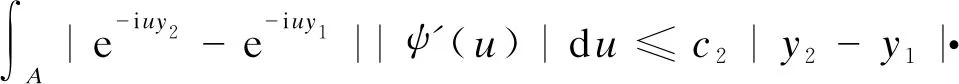
(6)

其中c3为常数.

当δ<1时，由引理1与式(4)可知:

其中c4为常数.

当δ<1时,

(7)

结合式(6)和式(7)可知，对u∈A，当δ≠1时，有

(8)

其中常数c5=max(c3,c2·c4).

(9)

结合式(2)，式(3)，式(8)和式(9)，推导出当δ≠1时，∀y1,y2∈[ε,)，有

因此存在常数c，使得

|ω(y1)-ω(y2)|≤c|y1-y2|δ′.

其中阶δ′=min(δ,1). 定理1中的1)得证.

3 定理1中2)的证明

当δ=1时，对式(2)中的第一部分I1同样有式(3)成立.为估计第二部分I2，将积分区域分为

当u∈A′时，由于

故存在常数c7，使得

(10)

(11)

其中常数c8=4M.

结合式(2)，式(3)，式(10)和式(11)知:当δ=1时，∀y1,y2∈[ε,)，有

4 说 明

在定理1的证明过程中，为估计第二部分I2，若采取不同积分区域的分割方法，依旧无法在不区分δ取值的情况下，得到Lipschitz连续性的阶.例如将积分区域分为

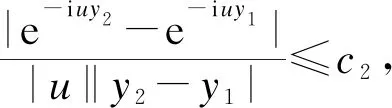
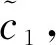
(12)

|e-iuy2-e-iuy1|≤c2|u||y2-y1|≤c2(|u||y2-y1|)min(δ,1).

若|u||y2-y1|>1，有

(|u||y2-y1|)min(δ,1)>1.

但是

|e-iuy2-e-iuy1|≤2.

由于

再由引理1知:

(13)

3) 结合式(2)，式(3)，式(12)和式(13)，当δ>1时，对任意的y1,y2∈[ε,)，有

也就是说当δ>1时，对任意的ε>0，ω(x)在[ε,)中Lipschitz连续的阶为δ′=1=min(δ,1).这也验证了定理1成立.