TCP/AWM网络系统的H∞拥塞跟踪控制

井元伟， 亓雪蕾， 申金栋， 井江山

(东北大学 信息科学与工程学院， 辽宁 沈阳 110819)

自有互联网出现以来，如何避免网络拥塞、提升网络性能一直是人们致力追求的目标.在互联网中广泛使用的数据传输协议是端到端传输控制协议(transport control protocol, TCP)，它能够有效地避免网络崩溃[1].而能保证端到端数据传输队列稳定到期望值的是一类叫作主动队列管理(active queue management, AQM)的算法，出现于20世纪末[2].将二者结合的TCP/AQM系统可实现合理的资源利用、可接受的数据包丢弃及稳定可靠的网络运行[3].目前，已提出了许多AQM方案.基于研究方法的不同，主要有由计算机学者发展的启发式方法，基于对策论等数学工具的方法和基于控制理论的方法等[4].

早在20世纪末和21世纪初，就有学者基于一定的假设提出了各种模型[5-10].这些模型各有其特点，如Mathis等[5]基于某些简化假设使得模型简单易于设计，但这些假设也易引起显著的误差；Kelly等[6]和Low等[7]的模型更接近实际系统但却不具备可扩展性；Ajmone[8]的偏微分方程形式的TCP模型较好地刻画了大规模网络，但过于复杂，不易于分析.而Misra等[9]提出的流体流模型可以很好地分析TCP/AQM系统的性能，为TCP/AQM系统的数值分析提供了理论基础.Hollot等[10]提出了改进的简化流体流模型，使其更便于应用，是目前广泛使用的TCP/AQM网络系统拥塞控制研究的模型之一[1]，并由此产生了许多新的AQM方案.诸多方案中应用了线性化技术或非线性控制技术等控制理论分析与设计方法，包括广义预测控制、T-S模糊控制、模型预测控制、最优控制、H∞控制、PI控制、滑模控制、数据驱动控制、逆推控制等控制技术.

主动队列管理算法是基于链路的控制算法.其拥塞控制算法部署在路由器中，可以直接判断网络是否拥塞，但是其无法直接控制数据包的发送速率.在2007年，Barbera等[11]提出了一种叫作主动窗口管理(active window management, AWM)的新模型机制，这种控制机制与各端节点的协议兼容，不需要修改端节点的控制算法.该方法将拥塞控制算法部署在网关之中，不需要通过丢包、吞吐量的改变来感知网络状态，即可直接控制源端的发送速率.在单瓶颈链路下，AWM机制更具优势.文献[12-14]对于AWM机制进行了研究，但主要集中在对网络性能的分析、比较上，并没有从控制理论的角度对AWM机制进行分析和研究.在2016年，首次有研究者将AWM机制同控制理论相结合，提出了一种基于PID的窗口控制规律[15].所设计的控制算法在兼容所有版本的TCP协议的情况下，使得窗口的变化规律可设计，而不是简单的AIMD的方式.但是PID控制算法参数设置固定，当网络情况变化时，算法的性能会下降.

考虑到系统的非线性特性，采用back-stepping方法进行控制器的设计，而对于外部干扰，采用H∞性能函数进行处理，得到TCP/AWM网络系统的稳定性条件.

1 TCP/AWM网络系统模型

考虑如下单路由TCP/AWM网络系统动态模型[11]:

(1)

式中:W(t)为以数据包个数为度量的TCP源端窗口大小；q(t)为以数据包个数为度量的路由器瞬时队列长度；N(t)为TCP网络负载因子(即激活的TCP会话数)；C为以数据包个数为度量的链路带宽；Tp为传播时延；u(t)为待设计的窗口变化率.

近年来，越来越多的基于用户数据报协议(user datagram protocol, UDP)的一些应用出现在TCP通信网络中.在实际的网络中，运行在用户数据报上的UDP流会干扰TCP流的正常传输.为了能更准确地建立数学模型，考虑在常值链路带宽的基础上，减去UDP流所带来的外部干扰，以此来表示某一时刻的链路容量.

受文献[16-17]的启发，考虑UDP流的干扰，将描述发送窗口大小和路由器队列长度的TCP/AWM模型，即式(1)扩展为

(2).

(3)

式中:d(t)为由UDP流带来的外部干扰；R(t)为往返传播时间，各项符号表达的意义同式(1).

由于网络窗口对于大多数人来说是一个相对虚拟的概念，并考虑到速率与窗口之间的关系[17]，可以用源端的发送速率r(t)来描述窗口的变化:

(4)

综合式(2)～式(4)，可以得到基于r(t)和q(t)的新方程:

(5)

其中，

令x1(t)=q(t)，x2(t)=r(t)，于是，式(5)可以表示为

(6)

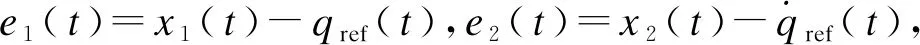
(7)

式中：ε=e1(t)+qref(t)+TpC；qref(t)为期望的队列长度.

2 Backstepping控制器设计

在本节中，将给出系统(7)的控制器设计过程.系统(7)针对状态变量具有严格下三角结构，故可以应用backstepping设计这一非线性控制方法，与H∞性能相结合，设计一种H∞拥塞跟踪控制器，使得系统的输出可以跟踪期望的队列长度.下面给出跟踪问题可解的结果.

定理 1如果存在状态反馈控制律u=u(t)，使得闭环系统满足以下两个条件，则式(7)的H∞跟踪问题是可解的:

i.所得到的闭环系统(7)的跟踪误差z1(t)稳定.

ii.闭环系统是L2稳定的，即对于任意初始条件存在一个非负常数φ(x0)满足

其中，T>0,γ>0,d∈L2[0,T).

根据backstepping方法的设计思想，首先考虑系统(7)中关于状态变量x1的子系统，对其进行控制器设计，然后在虚拟控制器的基础上设计控制器u(t).为此，定义如下的状态变换:

(8)

其中，α为待设计的虚拟控制器.于是有，

(9)

针对系统(7)采用backstepping方法进行稳定控制器设计.由于系统(7)有2个子系统，于是设计过程分为2个步骤.

步骤 1 系统(7)的第一个子系统可写为

(10)

这一步骤的目的是设计虚拟反馈控制器α使得z1→0.为此，选取Lyapunov函数:

(11)

将V1沿着子系统(10)对时间求导数，得

(12)

进而，有

(13)

选择一个适当的虚拟控制律:

(14)

将式(14)代入式(13)，可得

(15)

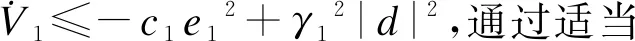
步骤 2 系统(7)的第二个子系统可写为

(16)

进一步，有

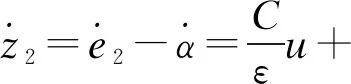
(17)

其中:

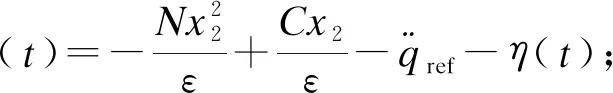
在这一步，目的是要设计一个状态反馈控制器使得状态方程在e2=0处渐近稳定.

构造如下的Lyapunov函数:

(18)

将V沿着子系统(10)和(16)对时间求导数，得

(19)

进一步，有

(20)

其中:υ(t)=ϑ(t)-ω(t)ψ(t);γ2=γ12+γ22.

根据式(20)的结构，可以设计如下的反馈控制律:

(21)

以使V<0.其中，c2是正的设计参数.

将式(21)代入式(20)，可得

(22)

为了验证系统的H∞性能，将式(22)转化为

(23)

其中，c10=c1-1>0.

对式(23)两边求积分，有

(24)

整理得

(25)

由式(25)可以看出，定义的条件ii成立.

由上述的推导分析过程可知，在所设计的逆推反馈控制器作用下，系统(6)渐近稳定.也就是说，系统(2)实现了主动窗口管理拥塞控制，可以达到期望的队列长度和适当的窗口大小.

3 仿真分析

基于改进的扰动误差模型给出相应的两组仿真.在第1组仿真中，对相同参数下的仿真结果逐一进行了分析；在第2组仿真中，针对改进的TCP/AWM模型，在不同的扰动情况下，给出了仿真结果.

仿真1:系统的各参数取值为

N=100,C=1 250,Tp=0.01,qref=200,x0=[400 0],c1=15,c2=30,γ1=40,γ2=10.

在本组仿真中，以d=10为例，对仿真结果进行分析.控制律u随时间的变化情况如图1所示.

由图1可以看出，控制律u从0.3 s开始稳定，并且在其后的时间段内一直处于稳定状态，系统的收敛速度非常快，可以快速稳定队列长度.由图1还可以看出，在d=10的情况下，控制律u最后稳定到0.这表明，在有少数UDP流占据链路带宽的情况下，并不影响源端对于TCP流的正常发送，亦即影响并不明显.

图2给出了在d=10时，队列跟踪误差e1随时间的变化情况.

由图2可以看出，当d=10，C=1 250时，跟踪误差最终稳定到零.这表明当外部扰动比较小时，瞬时队列q(t)可以成功地跟踪期望队列，即所设计控制器是有效的.

仿真2:本组仿真的主要目的是为了对改进系统模型的有效性进行验证.在本组仿真中用到的系统参数和设计参数同上一组仿真.此组仿真主要为了对比d分别等于1，10，100和500时，控制律和跟踪误差随时间变化的情况.

不同d值下控制律随时间变化的情况如图3所示.

由图3可以看出，在不同d值下，控制律随时间变化的整体趋势相同，这说明基于改进的TCP/AWM模型所设计的backstepping控制器具有很好的抗干扰能力.为了能进行进一步的分析，对图3的矩形框选部分进行了等比例放大，如图4所示.

由图4可以看出，对应不同的d值，4种情况下的仿真结果在同一坐标中大部分还是处于交叠状态.但是，在转折点处可以看到，4种情况下的曲线是处于分离状态.也就是说，控制律在系统中有外部扰动存在时，整体波动不大，系统的鲁棒性良好.

当d分别等于1，10，100和500时，队列跟踪误差随时间变化的情况如图5所示.

由图5可以看出，跟踪误差对不同d值并不敏感，因为除了转折处和稳定后能清楚看出没有交叠之外，仿真结果的交叠现象比较明显，而且在稳定后，基本上都稳定到了e1(t)=0处.为了对仿真结果进行更深层次的分析，图6对图5中的矩形框选部分进行了局部放大，可以更清楚地看到转折点处随时间的变化情况.

由图6可知，在0.06 s之前，4种情况下的仿真结果处于交叠状态，但并不是完全重合；在0.06 s之后，4种情况下的仿真结果开始存在不同程度的波动.其中d=500时波动程度最小，但是此时UDP流占据了将近一半的链路带宽.不同d值下队列跟踪误差的局部放大图如图7所示.

由图7可以看出，d=1时的跟踪效果最好.其次是d=10时，随着外部扰动增加，跟踪效果越来越差.当存在外部扰动时，所设计的控制器为了抵消其带来的影响，损失了一部分能量，这也导致瞬时队列没有足够的能力衰减至期望的队列长度，这种影响会随着外部扰动的增加而更加明显.

4 结 论

1) 本文基于TCP/AWM机制，给出了一个改进的TCP/AWM网络模型，为了达到跟踪控制的目标，利用误差变换将改进后的模型转化为等效误差模型.考虑到系统的非线性特性和存在UDP流等外部干扰的情况，将backstepping方法和H∞控制相结合，设计了H∞拥塞跟踪控制器.仿真结果表明，所设计的控制器，在外部扰动较小时，能够成功跟踪控制目标，而在外部扰动较大时，为抵消外部干扰的影响会损失一部分能量，只能跟踪到控制目标附近，此时控制器仍然有效.

2) 这一研究思路和所得结果不难扩展到多路由的情况，同时也可以以其他模型为基础，将多个子系统模型并联组合构成多路由网络系统.然后，采用先进控制技术设计控制器，为TCP/AWM系统提供主动窗口管理方案.