碳排放约束下双渠道供应链定价博弈策略
司凤山, 王 晶, 戴道明, 王玉玲
(1.安徽财经大学 管理科学与工程学院, 蚌埠 233030;2.中南民族大学 经济学院, 武汉 430073)
为减轻环境污染,政府有必要对企业实施碳排放约束政策,迫使企业节能减排以提高资源利用率.目前,学界已对碳减排、碳限额、碳交易等方面的内容进行深入研究.
关于碳减排和碳限额研究:杨亚琴等[1]研究政府对企业实施强制碳减排问题,建立强制碳减排机制下企业生产优化模型和碳减排博弈模型,给出实施碳减排政策的有效措施;陈伟达等[2]在碳排放限额情况下,探究再制造品新服务模式对制造商价格决策的影响;张李浩等[3]研究碳排放限额政策对双寡头企业定价和碳排放决策的影响,给出考虑经济和环境因素基础上最优碳排放限额政策;Ding等[4]考虑环境承受能力和碳排放限额约束情形,分析政府激励机制、供应链成员合作机制对供应链价格转移、价值转移和利润分配的影响;何华等[5-6]通过构建博弈模型探讨碳排放限额政策、碳排放限额与交易政策、碳排放限额与交易政策及绿色技术投入对企业最优定价、最优产量和最优利润的影响.
关于碳排放限额在闭环或多级供应链中的应用研究:张杰芳等[7]建立有无碳排放限额情形下零售商回收的闭环供应链博弈模型,分析集中决策和分散决策下的最优策略;Zhang等[8]在碳排放限额约束下,研究由制造商、零售商和回收商构成的闭环供应链系统中碳排放限额约束对最优策略和系统均衡的影响;Xu等[9]分析闭环供应链中废旧产品回收水平的不确定性和碳排放限额约束对降低成本和碳排放决策的影响;Qi等[10]研究碳排放限额下由1个供应商和2个零售商组成的两级订货供应链系统,探究分散决策模式下最优定价策略和经营策略;陈晓红等[11]构建由1个制造商和1个零售商组成的供应链模型,分析集中决策和分散决策中碳排放限额交易机制下碳交易价格对碳减排的影响.
关于碳排放限额和碳交易研究:朱慧贇等[12]在碳排放限额和碳交易政策约束下,构建企业制造和再制造的二阶段生产决策模型,探究碳排放限额和碳交易政策对企业再制造、定价、碳排放量和利润的影响,给出最优的新产品和再制造产品的生产策略;支帮东等[13]在考虑碳排放限额和交易机制下,构建碳减排Stackelberg博弈模型,给出最优碳减排策略;曾伟等[14]构建碳排放限额和碳交易机制下两级供应链联合经济批量模型,分析碳排放限额和交易机制等因素对供应链决策、碳排放总量和成本的影响;徐贤浩等[15]在碳排放限额约束和碳交易机制基础上,分析三级绿色供应链最优策略,给出集中决策和分散决策下最优订购量、制造商最优绿色减排水平和供应商最优绿色水平,分析碳排放限额和碳交易对最优决策的影响;汪明月等[16]基于碳排放权交易构建有无成本分担的分散决策模型和集中决策模型,借助微分对策方法对比分析不同模型均衡策略,探究低碳技术创新对碳减排收益的影响;王会会等[17]通过构建博弈演化模型分析碳排放限额、碳减排投入和“搭便车”行为对制造商、零售商和政府决策的影响,并提出具体博弈策略.
综上所述,对碳减排博弈模型的构建和分析、寡头企业博弈中碳排放限额对碳排放和定价策略的影响、闭环或多级供应链中碳排放限额约束对最优策略的影响、碳排放限额约束和碳交易机制的结合对最优策略的影响等方面的研究较为普遍.但对于双渠道供应链中,制造商和零售商同时受到碳排放限额约束时的定价问题鲜有涉及.基于此,本文针对碳排放限额约束下双渠道供应链中产品定价问题展开研究,以制造商利润和零售商利润最大化为研究目标,通过构建拉格朗日函数和分析Karush-Kuhn-Tucker(KKT)条件,给出不同情形下最优定价策略并对比分析,重点探讨碳排放限额对最优策略的影响.
1 双渠道博弈模型构建
在1个制造商和1个零售商构成的双渠道供应链博弈模型中,制造商单位产品的生产成本为c,以直销价p1进行线上销售,同时以批发价w向零售商供货进行线下销售,零售价为p2.直销渠道和零售商渠道的产品需求量分别为q1和q2.另外,制造商在生产过程中产生碳排放,单位产品的碳排放量为em,总碳排放量为Em.零售商在运输和销售等过程中也产生碳排放,单位产品碳排放量为er,总碳排放量为Er.为实现供应链绿色生产和运营,政府为制造商和零售商分别设定碳排放限额,制造商碳排放限额为Em0,零售商碳排放限额为Er0.基于以上描述,双渠道供应链结构如图1所示.

图1 碳排放限额约束下双渠道供应链结构图Fig.1 Structural diagram of dual-channel supply chain under carbon emission limits constraints
双渠道产品需求函数分别为
q1=a-α1p1+β1p2
(1)
q2=a-α2p2+β2p1
(2)
式中:a为产品潜在最大需求量;αi为价格敏感系数;βi为交叉价格敏感系数,a,αi,βi>0,i=1,2.由于渠道自身价格对其需求量影响较大,所以αi>βi.为便于分析和计算,令α1=α2=α;β1=β2=β;且α>β>0.
2 模型求解与策略分析
考虑制造商是领导者、零售商是跟随者的Stackelberg博弈.制造商首先确定直销价p1和批发价w,零售商在此基础上确定零售价p2.在以下分析过程中:下标s为Stackelberg博弈下策略值;上标*为最优策略;上标a1、a2、b1、b2为制造商和零售商是否受碳排放限额约束的组合情形;∏为利润.
制造商和零售商都以追求各自利润最大化为目标,两者利润函数分别为
∏m(p1,w)=(p1-c)q1+(w-c)q2
(3)
∏r(p2)=(p2-w)q2
(4)
制造商和零售商碳排放量Em和Er分别为
Em=(q1+q2)em
(5)
Er=q2er
(6)
制造商和零售商受到碳排放限额约束时的模型分别为
(7)
(8)
显然,模型(7)和模型(8)属于约束最优化问题,分别构造拉格朗日函数为
Lm(p1,w,λ1)=∏m(p1,w)+λ1(Em0-Em)
(9)
Lr(p2,λ2)=∏r(p2)+λ2(Er0-Er)
(10)
式中:λ1≥0和λ2≥0为拉格朗日乘子.
证得∏r(p2)是关于p2的严格凸函数,且不等式约束条件q2er≤Er0是凸的.因此,模型(8)为凸规划问题,其最优解由KKT条件唯一确定.
由一阶最优化条件得到最优零售价为
(11)
当λ2=0时,即零售商不受碳排放限额约束,则最优零售价为
(12)
当λ2>0时,根据互补松弛条件可知
Er0-q2er=0
(13)
由式(2)、式(11)和式(13)得到
(14)
将式(14)代入式(11)得到
(15)
分4种情形讨论Stackelberg博弈下制造商和零售商最优价格和最优利润.
情况a:零售商碳排放量小于等于碳排放限额(Er≤Er0),即零售商不受碳排放限额的约束(λ2=0).
情形a1:制造商碳排放量小于等于碳排放限额(Em≤Em0),即制造商不受碳排放限额约束(λ1=0),此种情形λ2=0,λ1=0,即零售商和制造商都不受碳排放限额约束.
情形a2:制造商碳排放量大于碳排放限额(Em>Em0),即制造商受碳排放限额约束(λ1>0),此种情形λ2=0,λ1>0,即零售商不受碳排放限额约束,而制造商受到碳排放限额约束.
情况b:零售商碳排放量大于碳排放限额(Er>Er0),即零售商受到碳排放限额约束(λ2>0).
情形b1:制造商碳排放量小于等于碳排放限额(Em≤Em0),即制造商不受碳排放限额约束(λ1=0),此种情形λ2>0,λ1=0,即零售商受到碳排放限额约束,而制造商不受碳排放限额约束.
情形b2:制造商碳排放量大于碳排放限额(Em>Em0),即制造商受到碳排放限额约束(λ1>0),此种情形λ2>0,λ1>0,即零售商和制造商都受到碳排放限额约束.
2.1 情况a定价策略
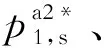
证明:在情况a中,当λ2=0时,将式(12)代入式(3),证得∏m(p1,w)是关于p1和w的严格凸函数,并且不等式约束条件(q1+q2)em≤Em0是凸的.因此,模型(7)为凸规划问题,其最优解由KKT条件唯一确定.

(16)
(17)
将式(16)和式(17)代入式(12)可得
(18)
将式(16)至式(18)分别代入式(3)和式(4)得到制造商和零售商的最优利润分别为

(19)
(20)
至此,命题1证毕.根据命题1,可得出如下结论.
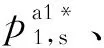

此外,还得到如下推论.
推论1:1) 当λ2=0,λ1=0时,Stackelberg博弈存在最优策略,满足条件
(21)
(22)
2) 当λ2=0,λ1>0时,Stackelberg博弈存在最优策略,应满足式(21)和条件
(23)
证明:当λ2=0时,由互补松弛条件可知Er0-q2er≥0,将式(16)和式(18)代入其中可得式(21).
1) 当λ1=0时,根据互补松弛条件可知Em0-(q1+q2)em≥0,将式(16)和式(18)代入其中可得式(22).
2) 当λ1>0时,根据互补松弛条件可知Em0-(q1+q2)em=0,将式(16)和式(18)代入其中可得
(24)
由于式(24)中分母大于零,所以分子必须大于零,即式(23)成立.
至此,推论1证毕.根据命题1和推论1,得到如下结论.
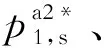
结论3表明,当零售商不受碳排放限额约束且制造商受碳排放限额约束时,制造商碳排放限额增加对制造商、零售商和消费者都有利.
2.2 情况b定价策略


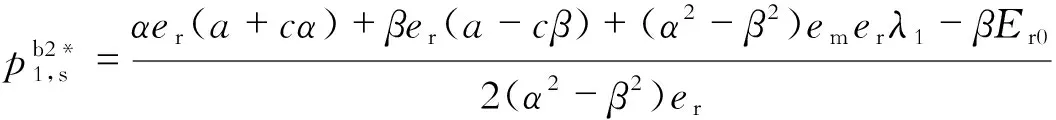
(25)
(26)
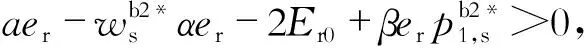
(27)
式中,ε>0且ε→0.
另外,将式(25)至式(27)分别代入式(3)和式(4)可以得到制造商和零售商最优利润分别为
(28)
(29)
至此,命题2证毕.根据命题2,得出如下结论.
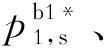


此外,还得到如下推论.
推论2:1) 当λ2>0,λ1=0时,Stackelberg博弈存在最优策略,满足条件为
(30)
2) 当λ2>0,λ1>0时,Stackelberg博弈存在最优策略,满足条件为
Em0<
(31)
证明:当λ2>0时,根据互补松弛条件得Er0-q2er=0,将式(25)和式(26)代入其中,验证可知等式成立.
1) 当λ1=0时,根据互补松弛条件可知Em0-(q1+q2)em≥0,将式(25)和式(26)代入其中可得式(30).
2) 当λ1>0时,根据互补松弛条件可知Em0-(q1+q2)em=0,将式(25)和式(26)代入其中可得
λ1=[-2αerEm0+em((α+β)(a-cα+cβ)er+
(32)
因为式(32)分母大于零,则分子必须大于零,得到式(31)成立.
至此,推论2证毕.
当λ2>0,λ1>0时,将式(31)分别代入式(25)至式(27)得到
(33)
(34)
(35)
由式(33)至式(35)得到如下结论.
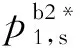

另外,由于制造商和零售商最优利润表达式过于复杂,所以下一节数值仿真研究情形b1和情形b2的最优利润与Em0和Er0的增减关系.
3 数值仿真及对比分析
3.1 碳排放限额对最优利润的影响
依据文中约束条件,模型中一组参数取值为:a=100;α=0.6;β=0.4;Em0=500或者Em0=200;Er0=50;c=5;em=3;er=1;ε=0.01.
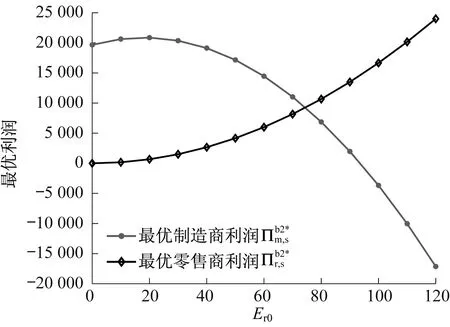
1) 在情形b1中,根据推论2中1)可得,存在最优策略条件为Em0≥347.50,此处取Em0=500,确保Em 图2 情形b1中Er0对最优利润的影响Fig.2 Effect of Er0 on optimal profits in case b1 2) 在情形b2中,根据推论2中2)可得,存在最优策略的条件为Em0<347.50,此处取Em0=200以确保Em>Em0,即制造商受到碳排放限额约束.零售商碳排放限额Er0对最优利润的影响如图3所示. 图3 情形b2中Er0对最优利润的影响Fig.3 Effect of Er0 on optimal profits in case b2 3) 在情形b2中,固定零售商碳排放限额Er0=50,确保Er>Er0,即零售商受到碳排放限额约束.根据推论2中2)得到制造商碳排放限额取值范围为0≤Em0<347.50.制造商碳排放限额Em0对最优利润的影响如图4所示. 图4 情形b2中Em0对最优利润的影响Fig.4 Effect of Em0 on optimal profits in case b2 综合2.1节、2.2节和3.1节的内容,可以得到不同情形下制造商和零售商最优价格和最优利润对比分析结果,见表1.表中情形b1和b2均存在:1) 零售商最优利润不变;2) 零售商碳排放限额越大,零售商最优利润越大;3) 存在最优零售商碳排放限额使得制造商最优利润最大. 表1 不同情形下制造商和零售商最优策略对比分析Table 1 Comparative analysis of optimal strategies of manufacturers and retailers in different situations 从表1可知,首先,制造商和零售商最理想策略是不受碳排放限额约束,此时不但两者都能获得较高利润,而且较低销售价格对消费者也有利;其次,如果迫于政府政策和环保压力,制造商或零售商必须有一方受到碳排放限额约束,那么零售商受到碳排放限额约束更佳,此时较低最优价格对消费者有利,而且制造商还能获得较高利润,但是必须采用协调机制使零售商共享制造商收益,以便促使零售商尽力向政府争取较大碳排放限额;最后,当制造商和零售商同时受到碳排放限额约束时,较高最优价格对消费者不利,并且制造商难以获得满意收益,此时制造商和零售商同时向政府争取更大碳排放限额,不但对消费者有利,而且更有助于两者都获得高额利润,此时存在最优制造商碳排放限额和最优零售商碳排放限额使得制造商的最优利润最大. 针对双渠道供应链中碳排放限额约束问题,通过构建非线性规划模型分析制造商和零售商在Stackelberg博弈中的最优策略.讨论制造商和零售商是否存在碳排放限额约束的4种组合情形,给出每种情形最优策略存在的条件以及最优策略解析式,对比分析不同情形下最优价格和最优利润的差异,剖析制造商和零售商碳排放限额对最优策略的影响.研究表明,当零售商不受碳排放限额约束时,若制造商碳排放量超出碳排放限额将导致价格(直销价、零售价和批发价)上涨和利润(制造商利润和零售商利润)下降,这对消费者、制造商和零售商都不利.当零售商受到碳排放限额约束时,若制造商碳排放量超出碳排放限额将导致价格上涨和制造商利润下降,而零售商利润则保持不变,这对消费者和制造商不利,而零售商则不受影响. 在不同情形下,制造商和零售商利润变化较大,调节碳排放限额不能兼顾制造商和零售商都实现利润最优.为此,可设计协调机制在制造商和零售商之间实现收益共享,从而实现双赢,这是本文下一步将要研究的内容.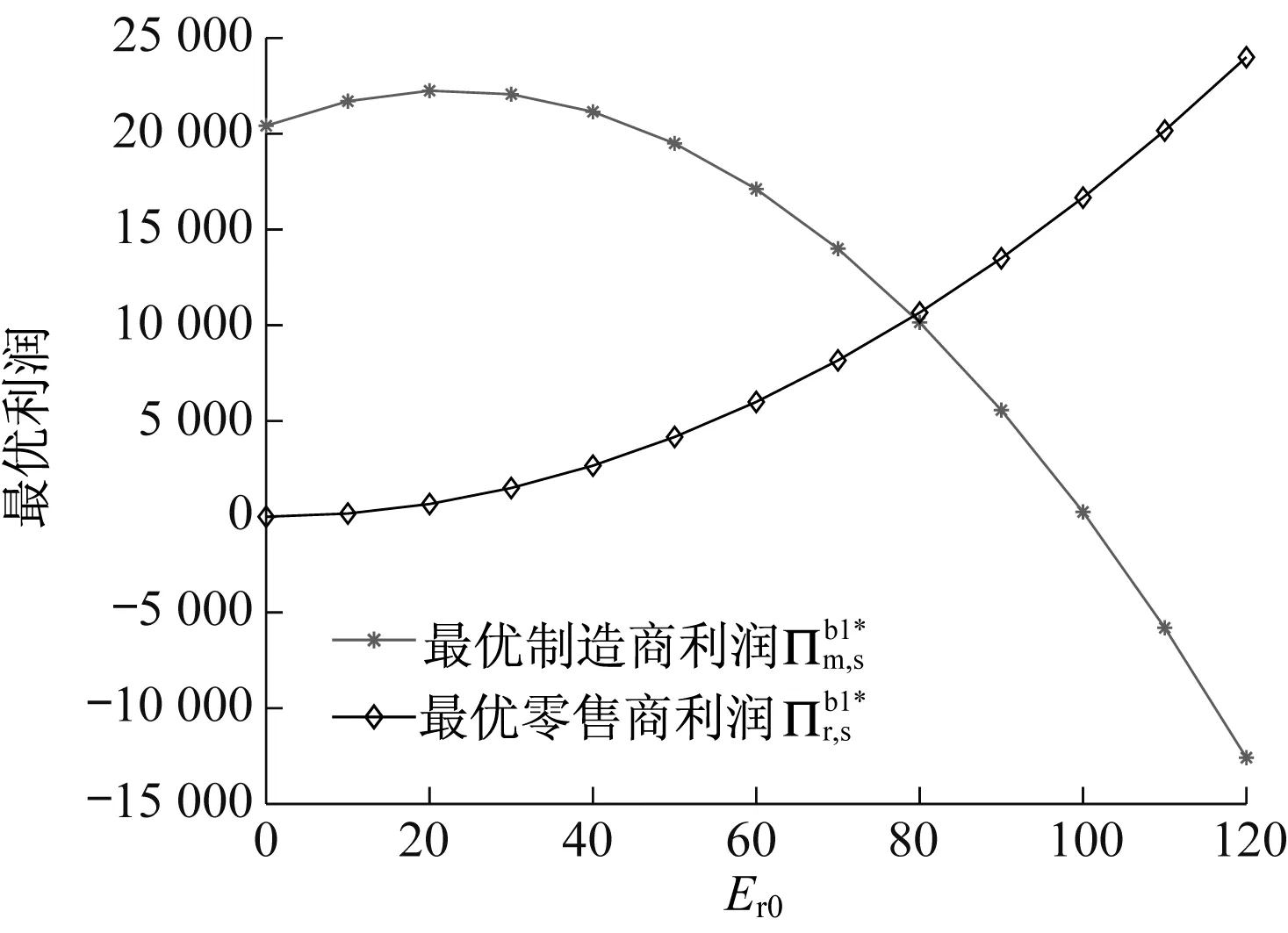



3.2 不同情形下的策略对比分析

4 结 语

