港口集装箱吞吐量预测方法研究

王 茁, 高 璐

(大连科技学院 交通运输学院, 大连 116052)

集装箱运输是现代化交通运输中占比最大的运输方式,以效率高、安全性好和快速便捷的特点成为运输国际货物的首选途径.我国在近几年开始大力投资港口、航道,并不断加大对其投、融资力度,这对集装箱运输业的发展起到催化作用.加入世贸组织后,我国水路运输发展非常迅猛,对港口进行合理规划的重要性逐渐凸显,而对港口集装箱吞吐量的准确预测是顺利完成港口规划的前提,直接决定其完成质量.

1 集装箱运输研究概述

1.1 我国港口集装箱运输现状分析

近年来,我国沿海大型港口开始偏向于增加深水泊位的数量,提高对吨位特别高的运输货轮的支持.2013年,深水泊位数量已经达到5 761个,是2003年(361个)的十几倍[1].同时,我国集装箱吞吐量长年保持稳定增长的状态.

根据港口集装箱吞吐量增长的特点,可以将其分为普通增长型、波动增长型和加速增长型3大类:1) 普通增长型港口,如上海港、天津港、大连港和海口港等,这类港口大都是我国传统大港,坐落于经济发达地区,其腹地经济的规模也往往很大,经济增长趋于平稳;2) 波动增长型港口,如烟台港、汕头港、连云港港等,往往是一些地区支线港,其规模较小、易受经济波动及周边港口竞争等多种影响,波动性更为明显;3) 加速增长型港口,如深圳港、宁波港、营口港等,多为开展集装箱业务时间比较短暂,但近十年来呈现出加速增长态势的港口,这些港口年均增长率都维持在40%以上[2].

1.2 集装箱吞吐量预测研究现状

2 常用预测分析方法

2.1 时间序列模型预测算法

时间序列模型预测算法是指采用历史数据以时间为维度进行建模,借助模型计算出待预测部分的数据.该算法基于以下假设:对事物发展起到影响作用的因素无论是在过去还是未来,都在持续地对其造成影响;事物的发展通常情况下不会出现太大的跳跃式波动,而是循序渐进地发展[10].常用的时间序列法可分为移动平均法、指数平滑法和趋势外推法,其优缺点见表1.本文选择指数平滑算法对吞吐量进行预测.

2.2 回归模型预测算法

回归模型预测算法是一种对事物间相关关系进行分析与提炼,并以这些共同点为联系建立数学模型的预测方法.根据回归模型中变量间的函数性质,将待研究事物变化的关系进行分析来获得相关模型.由于该算法拥有较高的可靠性与实用性,经常被用在各种工程实践的预测问题中.主要包括一元线性回归、多元线性回归和非线性回归3种预测模型[11].

2.3 灰色模型预测算法

灰色模型是整个灰色预测与控制的理论基础与预测工具.在对港口集装箱吞吐量的预测中,目前采用的灰色模型基本上还停留在最原始的GM(1,1)灰色预测模型[12],此模型使用范围广,预测精度较高,可用于动态分析和预测,在原始信息较少时可以获得较为精确的预测值.

2.4 集装箱吞吐量预测方法选择

本文拟用上述3种算法预测港口集装箱的吞吐量,在分析与对比的过程中得出每种算法的特点与适合预测的港口类型.基于大连港历史数据计算得出3种模型的预测精度,作为衡量预测方法是否适用于预测对象的一个重要指标.本文选用预测误差的方差和标准差来进行精度测定.预测误差的方差及标准差公式分别为

(1)

(2)

3 港口集装箱吞吐量预测实证

大连市是东北地区最大的沿海城市,大连港集装箱运输自20世纪80年代后开始进入快速发展阶段.1988年,位于大连港老港区西侧的杂货泊位升级改造成第一个集装箱专用泊位,大幅增加了大连港口的交通能力.随后在交通部的全国港口规划中,大连港被划定到全国四大深水港之一,成为东北地区对外贸易快速发展的枢纽,开通了欧洲、南非、美东、美西、地中海等5条运输干线.但从近几年的统计数据来看,大连港在全国集装箱运输体系所处的地位呈现出逐年下降的趋势.

大连港2013—2017年吞吐量数据见表2.采用这些数据对2018年港口吞吐量进行预测,港口吞吐量包括进出口及转口数据.

2)对于内雨带的传播机制而言,通过谐波分析发现,和重力波、Rossby波以及混合波均没有关系,内雨带的可能发展机制可能是由垂直风切变引起次级环流,其逆切变区低层的出流使得内雨带径向向外运动,而低层的水平风场和变形场会使得其形成其螺旋结构。

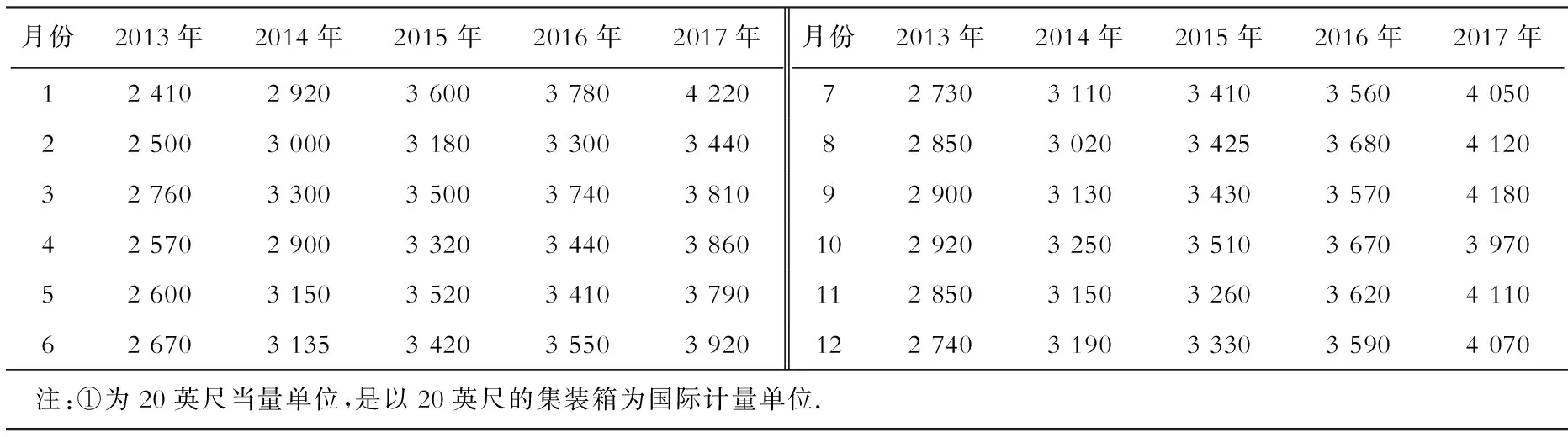
表2 大连港2013—2017年吞吐量数据Table 2 Throughput data of Dalian port from 2013 to 2017 万TEU①

3.1 基于时间序列模型的预测结果分析

以2013—2016年数据作为原始数据,采用指数平滑算法对大连港集装箱货运吞吐量进行预测.一次指数平滑法预测模型为

(3)

二次指数平滑法预测模型为

(4)

其中

(5)

由于港口集装箱吞吐量易受季节影响产生较大的波动,所以选择平滑系数α=0.9.将2013年1月的集装箱吞吐量周期记为t=1,计算预测序列S(1)值和S(2)值,见表3.

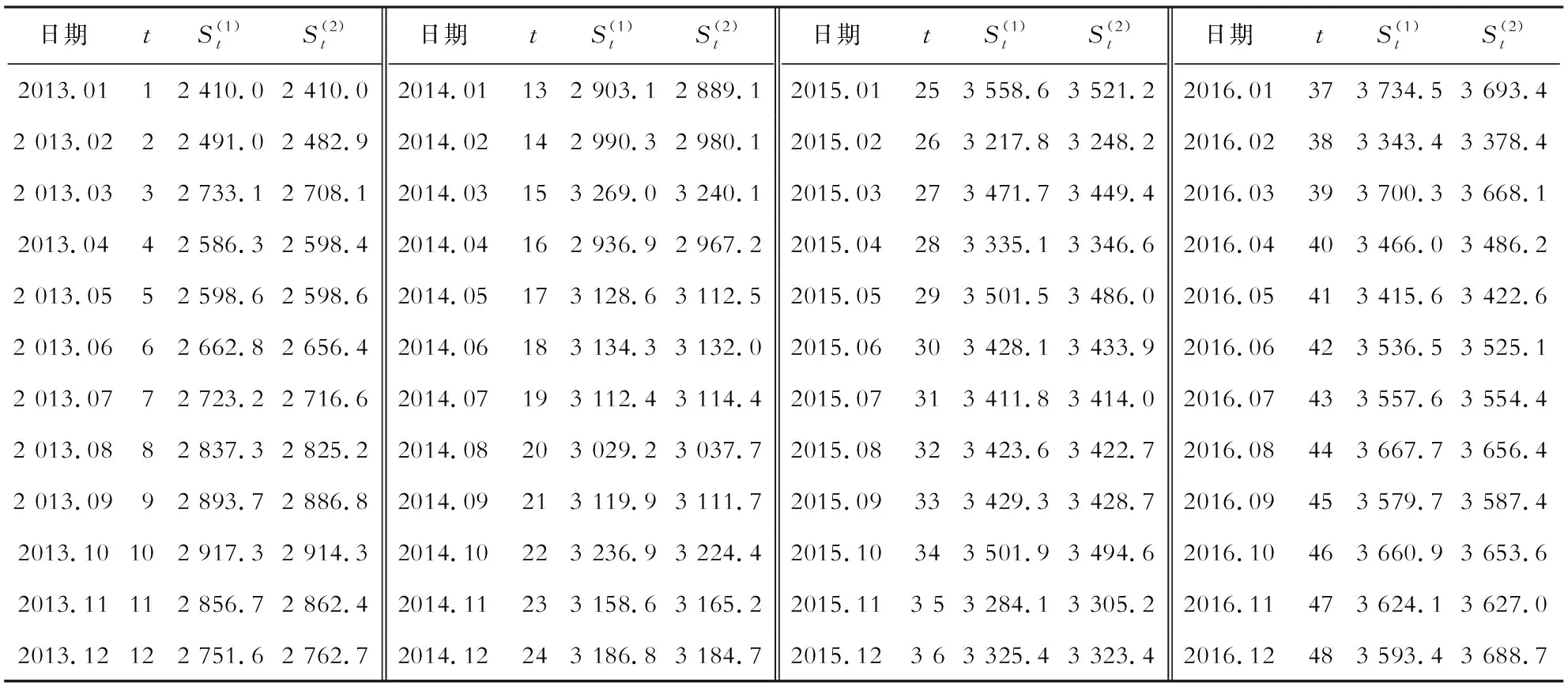
表3 时间序列模型一次与二次指数平滑值Table 3 First and second exponential smoothing values of time series model

图1 基于时间序列模型预测算法的港口集装箱吞吐量预测结果Fig.1 Prediction results of port container throughout based on time series prediction algorithm model

由图1可知,当港口集装箱吞吐量受多种因素影响而呈现出较大波动时,时间序列预测法不能很准确地预测到这种变化,此时预测结果误差较大.时间序列模型的预测精度测定值见表4,由表中数据计算可知,时间序列模型MSE=37 525.689 170,SDE=193.715 485.

表4 时间序列模型预测精度Table 4 Prediction accuracy of time series model

3.2 基于回归模型的预测结果分析

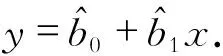
y=2 622.952+23.520x

对回归方程的拟合度进行分析,得出预测模型的总平方和SST=6 055 331.25,回归平方和SSR=5 699 224.948 437,判定系数R2=0.941 191,由于只考虑大连港吞吐量一个因素,方程的拟合精度较差.在信息较少的情况下可以用灰色模型以得到更为精确的结果,或者通过筛选出更多影响因素构建多元线性回归方程来获得更高精度.

对回归方程模型做显著性检验,计算得到预测模型F值为11.14,在显著性水平α=0.005时临界值Fα为12.78,故认为吞吐量与时间存在某种线性关系.利用回归方程对2018年港口集装箱吞吐量进行预测,结果如图2所示.

图2 基于回归模型预测算法的港口集装箱吞吐量预测结果Fig.2 Prediction results of port container throughput based on regression model prediction algorithm

由于只用时间作为唯一的自变量,预测精度不高,所以当实际数据遇到季节、政治或经济危机等其他影响因素时,一元线性回归模型的精度就会下降.此时最好分析一些其他可能的影响因素,如烟台港港口集装箱吞吐量、大连当月GDP总值或全国GDP总值等,以便得到更为精确的预测模型.回归预测模型的精度测定值见表5,可知回归预测MSE=36 827.521 670,SDE=191.904 981.

表5 回归模型预测精度Table 5 Prediction accuracy of regression model

3.3 基于灰色模型的预测结果分析

将2013—2016年数据作为原始数据,构建原始数列x(0),并求出其一阶累加值,将新生成的一阶累加数列命名为x(1).对于累加序列x(1),建立微分方程模型为

采用Matlab进行矩阵计算,得出a=-0.007 0,u=2 701.8,故微分方程结果为

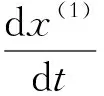
由微分方程可得G(1,1)预测模型为

采用灰色模型所得的预测值如图3所示.

图3 基于灰色模型预测算法的港口集装箱吞吐量预测结果Fig.3 Prediction results of port container throughput based on grey prediction model prediction algorithm

由图可知,灰色模型的预测结果与真实值相比波动更小,数据出现波动时的预测效果比前两种线性模型好.说明灰色模型在已知信息较少时也可以较为准确的得出预测值,虽然计算过程较为烦琐,但是模型的精确度更高,故灰色模型较适合对港口集装箱吞吐量进行预测.

3.4 3种预测模型预测结果比较

将3种模型的预测值与实际值对比分析如图4所示.从图4可以看出,时间序列预测模型与线性回归预测模型所得出的结果接近为一条直线,说明两者预测结果相近.由于集装箱吞吐量的值易受季节、经济情况与腹地经济发展等因素影响,其实际值往往波动较大,并不能很好地用线性关系拟合.而灰色模型采用对实际值做一阶累加后求微分方程的方法建模,在获取信息较少时,比其他线性模型相比具有更高的精度.将3种模型的精度进行对比,见表6,差值越小,说明精度越高.由表6数据可知灰色模型的预测值精度最好.

表6 3种模型精度值Table 6 Precision values of the three models

图4 3种预测模型算法预测结果Fig.4 Prediction results of three prediction model algorithms

对比分析时间序列模型、回归模型和灰色模型3种预测模型的预测结果可以发现:1) 对于港口运量增长较为平稳的普通增长型港口,3种预测模型都能取得很好的预测效果,其中,灰色模型只需较少的数据便可以达到很高的预测精度,回归模型需要的数据较多,但是可以很好地处理转折点的问题,但对数据要求较为苛刻;2) 对于加速增长型港口,由于数据增长较快,基于平均值的时间序列模型会出现较大的误差,其他2种模型更适用于这类港口的预测,其中灰色模型的样本不建议选的过长,可能会对预测精度起到不好的影响,多元回归模型在建立过程中寻找解释变量可能会更加困难,很多经济变量并不与港口的集装箱运量线性相关;3) 对于波动增长型的港口,传统的时间序列模型和回归模型没有办法考虑非量化因素的影响,而灰色模型对这种影响的判断也较弱,会出现较大的误差.此时采用RBF神经网络模型等基于神经网络与聚类分析的算法可能会有更好的效果.

基于上述实验结果可知,虽然大连港是平稳的普通增长型港口,但当港口集装箱吞吐量出现较大波动时,时间序列预测法误差较大,故本研究采用回归模型和灰色模型对大连港未来五年集装箱吞吐量进行预测,结果如图5所示,可以看出大连港未来五年集装箱吞吐量总体为上升趋势,且其吞吐量增长速度依旧在逐渐加快.整体吞吐量没有出现较大波动,继续向着平稳的方向发展.

图5 大连港未来五年集装箱吞吐量预测结果Fig.5 Prediction results of container throughput in Dalian port in next five years

4 结 语

本文在介绍集装箱吞吐量预测算法与理论的基础上,运用时间序列模型、回归模型与灰色模型3种方法对大连港集装箱吞吐量进行预测,通过对3种预测模型进行误差分析,得出3种模型适用的港口类型、研究结果为相关管理人员提供了一定的参考.