小区谷物联合收获机作业速度智能调控算法设计与仿真

邢高勇,毛罕平,王佳慧,眭 旸,彭海涛

(江苏大学 现代农业装备与技术教育部重点实验室,江苏 镇江 212013)

0 引言

农业育种小区是选育良种、进行品种对比试验的基地。小区收获是获得田间育种试验正确试验结果的最重要环节,直接影响良种的选育。小区收获不同于大田收获,育种试验田块中包含许多试验小区与试验品种[1],每个小区作物种子形态各异,成熟后作物的高度、密度、含水率等存在较大差异[2],要求操作人员需要具备熟练的操作技能和丰富的作业经验,能够根据实际的作物情况来不断地调整作业速度,合理控制喂入量,防止脱粒滚筒发生堵塞,以提高种子收获质量,保证育种试验结果的正确性。然而,实际小区作业时,大多数机手并非专业技术人员,接受专业培训较少且缺乏实际操作经验,对小区谷物联合收获机工况判断、故障排除与诊断的经验非常有限,导致脱粒滚筒过载堵塞的情况时有发生,从而导致种子严重损伤,影响试验结果。国内对于小区联合收获机的研究主要集中于种子籽粒的高脱净、低损伤、防混种,割台、脱粒滚筒、种箱的自净,以及小区测产、小区品种试验数据获取等方面,对于小区联合收获机作业速度自适应调控方面的研究还处于空白。

针对以上问题,以4LZZ-1.0型小区谷物联合收获机为对象,设计了一套基于模糊理论的作业速度智能调控算法,可根据脱粒滚筒的转速变化情况不断地调整作业速度,防止其脱粒滚筒发生堵塞,提高收获作业效率与质量。同时,建立了Simulink仿真模型,对算法进行了仿真试验验证。

1 调控方案设计

作业过程中,脱粒滚筒发生堵塞一般是由喂入量过大引起的,所以在作业过程中需将小区谷物联合收获机的喂入量控制在合理范围。在割幅、作物密度不变的情况下,喂入量与作业速度成正相关,可以通过调节作业速度将喂入量保持在脱粒滚筒的额定范围内,防止堵塞的发生,减少故障率,提高作业质量。

根据以上分析,调控算法以脱粒滚筒的转速变化及变化率作为系统调控依据,根据脱粒滚筒的转速变化情况,确定最佳作业速度,使喂入量保持在其额定范围内[3]。4LZZ-1.0型小区谷物联合收获机行走系统为阀控液压马达驱动,如图1所示。工作时,可以通过给定不同电压值调节伺服阀流量来控制液压马达的转速[4],液压马达通过升速齿轮与履带驱动轮连接,进而控制其作业速度。

图1 液压马达伺服控制原理Fig.1 Hydraulic motor servo control principle

所设计的调控系统通过调节小区谷物联合收获机作业速度维持脱粒滚筒转速的稳定,防止发生堵塞,提高种子收获质量。首先,通过模糊理论建立脱粒滚筒转速—作业速度模糊控制器,根据脱粒滚筒转速的变化情况确定期望作业速度,将期望作业速度作为模糊PID作业速度控制器的输入;根据期望作业速度调节伺服阀输入电压,控制伺服阀流量,调节马达转速,从而不断地调整小区谷物联合收获机的作业速度,使脱粒滚筒保持在正常状态,提高收获效率与质量。

图1中：PS为进油口压力(Pa),in为转速(r/min),Uf为反馈电压(V),θm为液压马达转速(rad/s)。

电液压伺服系统存在多重非线性因素,需要采用控制算法来提高系统的动态调节性能[5]。对于非线性系统,传统控制理论方法难以取得满意的动态特性,不易实现对液压伺服系统的实时在线高精度控制。本文通过模糊PID控制算法,根据脱粒滚筒转速的变化情况来确定期望作业速度,不断地调节伺服阀的输入电压,控制作业速度,使喂入量保持在脱粒滚筒的额定范围内,以防止堵塞情况的发生。图2为模糊PID控制算法结构。系统通过作业速度传感器采样获得其反馈值,然后将其与期望作业速度(给定值)进行比较,得到作业速度误差e及其变化率ec;对其进行模糊化处理得到模糊量,经过模糊推理、解模糊获得控制量u。

图2 模糊PID作业速度调控算法结构框图Fig.2 Structural block diagram of fuzzy PID working speed control algorithm

2 模糊控制器设计

2.1 脱粒滚筒转速—期望作业速度模糊控制器语言变量及其隶属度函数

脱粒滚筒转速—期望作业速度模糊控制器输入变量为脱粒滚筒转速误差e(k)及其变化率△e(k)模糊语言变量分别为E、EC,输出变量为期望作业速度,模糊语言变量为V。语言变量值均定为{正大、正中、正小、零、负大、负中、负小}7个等级,记作{PB、PM、PS、ZO、NB、NM、NS}。输入语言变量e(k)和△e(k)的基本论域为[-0.16,0.16]、[-0.015,0.015],输出变量V的基本论域为[0,3.2]。将输入语言变量E、EC和输出语言变量V对应到[-3,3]的论域,则输入变量e(k)和△e(k)的量化因子Ke、Kec及输出控制量V的比例因子K分别为

Ke=0.16/3=0.053

Kec=0.015/3=0.05

K=3.2/6=0.53

2.2 脱粒滚筒转速—作业速度模糊规则的建立

根据经验,在割幅、作物密度不变的情况下,喂入量与作业速度成正相关。作业速度增大,喂入量增大,脱粒滚筒负荷增大,滚筒转速降低;作业速度减小,喂入量减小,脱粒滚筒负荷减小,滚筒转速升高。据此来设计脱粒滚筒转速与期望作业速度的模糊规则表。

表1中,当脱粒滚筒转速变化语言变量E为NB(对应基本论域的-0.16)时,表示转速减小了额定转速的16%,此时系统停车,所以无论变化率为多少,模糊输出均为NB;语言变量E为PM、PB(对应基本论域的0.107、0.16)时,表示脱粒滚筒转速增加了额定转速的10.7%、16%,按照额定转速940r/min来计算,即增加100.6、150.4r/min,而脱粒滚筒空载转速在1000r/min左右。因此,正常状态下,即使上升到空载转速,增加的幅度也不可能有那么大,所以这两种情况下不论EC值为多少,输出值均为ZO。其他情况根据E、EC语言变量值来确定输出语言变量V的值。以语言变量E为NS,语言变量EC为PS为例说明,E为NS说明转速有所降低,EC为PS说明转速降低的趋势在减小,此时语言变量输出为ZO,即作业速度保持设定作业速度。

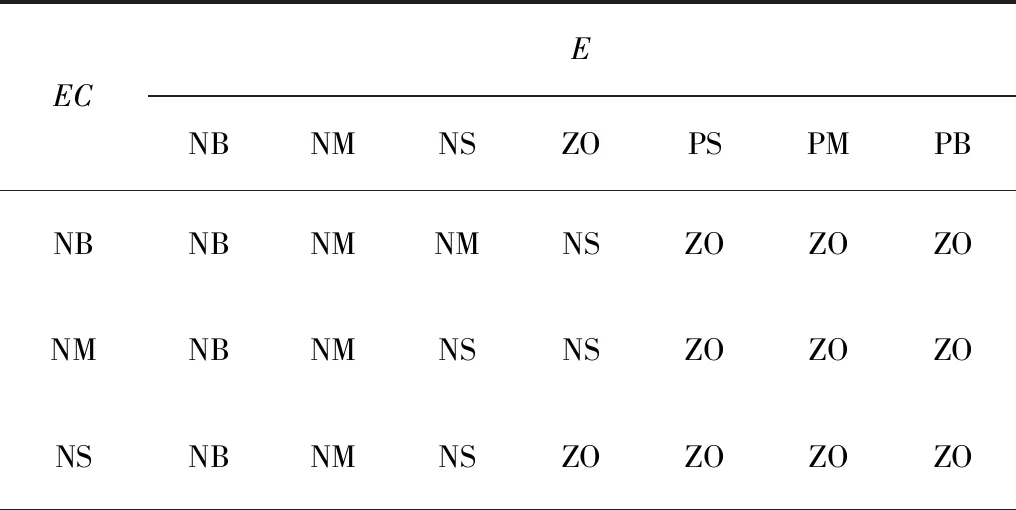
表1 脱粒滚筒转速—期望作业速度模糊规则表Table 1 Fuzzy rule table of threshing cylinder speed-expected working speed

3 模糊PID作业速度控制器的设计

3.1 模糊PID作业速度控制器语言变量及其隶属度函数

模糊控制器的输入变量分别为作业速度误差e1(k)与其变化率△e1(k),语言变量分别为E1、EC1,输出变量为ΔKP、ΔKI、ΔKD,语言变量分别为KP、KI、KD。语言变量值及符号同2.1节。其中,输入变量及输出变量的基本论域依次分别为[-3.6,3.6]、[-3.6,3.6]、[-0.3,0.3]、[-9,9]。将输入语言变量E1和EC1对应到[-3,3]的论域,输出语言变量KP、KI、KD对应到[-3,3]的论域,则输入变量e1(k)和△e1(k)的量化因子Ke1、Kec1及输出控制量△KP、△KI的比例因子K1、K2分别为

Ke1=3.6/3=1.2

Kec1=3.6/3=1.2

K1=0.3/3=0.1

K2=9/3=3

各语言变量中,NB采用高斯型隶属度函数,其他采用三角隶属度函数。

3.2 模糊规则的建立

根据PID控制参数对系统输出的影响及经验,得到控制参数在不同的|E|及|EC|状态下的原则如下：

1)当误差|E1|较大时,为提高系统响应速度,应尽快消除误差,KP取较大的值和KD取较小的值,为避免出现超调过大,取较小的KI值。

2)当误差|E1|处于中等大小时,为提高系统响应速度,取较小的KP值,KD和KI的值选择适中。

3)当误差|E1|较小时,为了能够消除静差、减小超调量、提高系统稳定性,应增大KI的值,减小KP的值;当|EC1|较小时,为增强系统抗干扰性能,应取较大的KD值,反之则取较小值。

4)误差变化率|EC1|越大,KP值越大,KI值越小,需结合误差大小考虑KP和KI值的变化;同时,可通过调整KD值来抑制过度变化、缩短调节时间。

根据以上原则结合“IF A AND B THEN C AND D”规则,在表2中给出了KP、KI、KD的控制规则。

表2 模糊PID控制规则表Table 2 Fuzzy PID control rules

4 仿真试验验证

4.1 小区谷物联合收获机行走系统数学模型的建立

小区谷物联合收获机行走系统主要由伺服阀带动控制液压马达流量来实现转速的控制,因此需要对这两个模块进行建模,获得输入电压与输出转速的关系。

1)伺服阀的建模。伺服阀的建模是为了建立其输入电压与输出流量的关系,可以通过求其传递函数得到。伺服阀的传递函数需要根据动力元件液压的固有频率大小确定[7-8],如果液压固有频率与伺服阀的频宽相近,伺服阀可近似看成二阶振荡环节,即

(1)

其中,KS为伺服阀流量增益[m3/(S·V)];GS是伺服阀在KS=1时的传递函数;ωS为伺服阀的固有频率(Hz);ξS为伺服阀阻尼比;U是伺服阀输入电压(V)。

2)阀控液压马达的建模。阀控液压马达建模是通过求其传递函数来建立输入流量与液压马达转速的关系,液压马达的传递函数可以根据式(2)液压控制阀的流量方程、式(3)液压马达流量连续性方程、式(4)液压马达与负载的力平衡方程这3个基本方程推导出来[8],即

qL=KqXV-KcPL

(2)

其中,qL为负载流量(m3/s) ;Kq为流量增益[m3/(s·m)];Kc为流量压力系数[m3/(s·Pa)];XV为阀芯位移(m);PL为负载压力(Pa)。

(3)

其中,Dm为液压马达排量(mL);θm为液压马达转速(rad/s);Ctm为液压马达总泄漏系数;βe为有效体积弹性模量(Pa);Vt为阀控液马达的总容积(L);t为时间(s)。

式(3)中,右边第1项是驱动液压马达转动需要的流量,第2项是液压系统总泄漏流量,第3项是液压系统总压缩流量,则有

(4)

其中,Bt为马达轴上总等效黏性阻尼系数;G为负载的扭转弹簧刚度(N/m);TL为外负载力矩(N·m);JL为负载上的转动惯量(kg·m2)。

对式(2)～式(4)中的方程进行拉普拉斯变换,消去中间变量qL、PL,可以求得阀芯位移XV、外负载力矩TL同时作用于液压马达时,输出转速与两者的关系,即

(5)

其中,ωh为液压固有频率(Hz);ξh为液压阻尼比;Kce为总流量压力系数[m3/(s·Pa)]。

根据式(5)可以求得液压马达转速θm对阀芯位移XV的传递函数为

(6)

所以,液压马达转速θm对伺服阀空载流量Q0的传递函数为

(7)

3)液压马达传递函数的求解。在式(1)、式(2)中通过建立伺服阀与液压马达的数学模型,分别得到了伺服阀流量Q0与电压U、液压马达转速θm与伺服阀流量Q0的传递函数,将式(1)、式(7)中两个传递函数相乘,消去中间变量Q0,即可得到液压马达转速θm与伺服阀输入电压U的传递函数,即

(8)

其中,ωh为马达的固有频率,可通过下式根据表3计算得到,即

表3 液压马达技术参数表Table 3 Hydraulic motor technical parameter table

(9)

ξh为液压马达阻尼比,计算式为

(10)

小区谷物联合收获机伺服阀型号为QDY15,固有频率ωS为500rad/s,阻尼比ξS为0.35,空载最大流量Qmax为18L/min,即3×10-3m3/s,最大伺服电压Umax为10V,根据式(11)可计算出伺服阀增益KS为0.3×10-4m3/(s·V),即

(11)

根据以上参数,最终确定液压马达转速θm对伺服阀电压U的传递函数为

(12)

4.2 模糊PID作业速度调控算法的仿真试验验证

为了对算法进行仿真试验验证,本文参考了文献[9]中大田收获的试验数据,以该文献中脱粒滚筒的试验数据(见表4)作为脱粒滚筒转速—作业速度模糊控制器的输入,输出期望作业速度给模糊PID作业速度控制器。

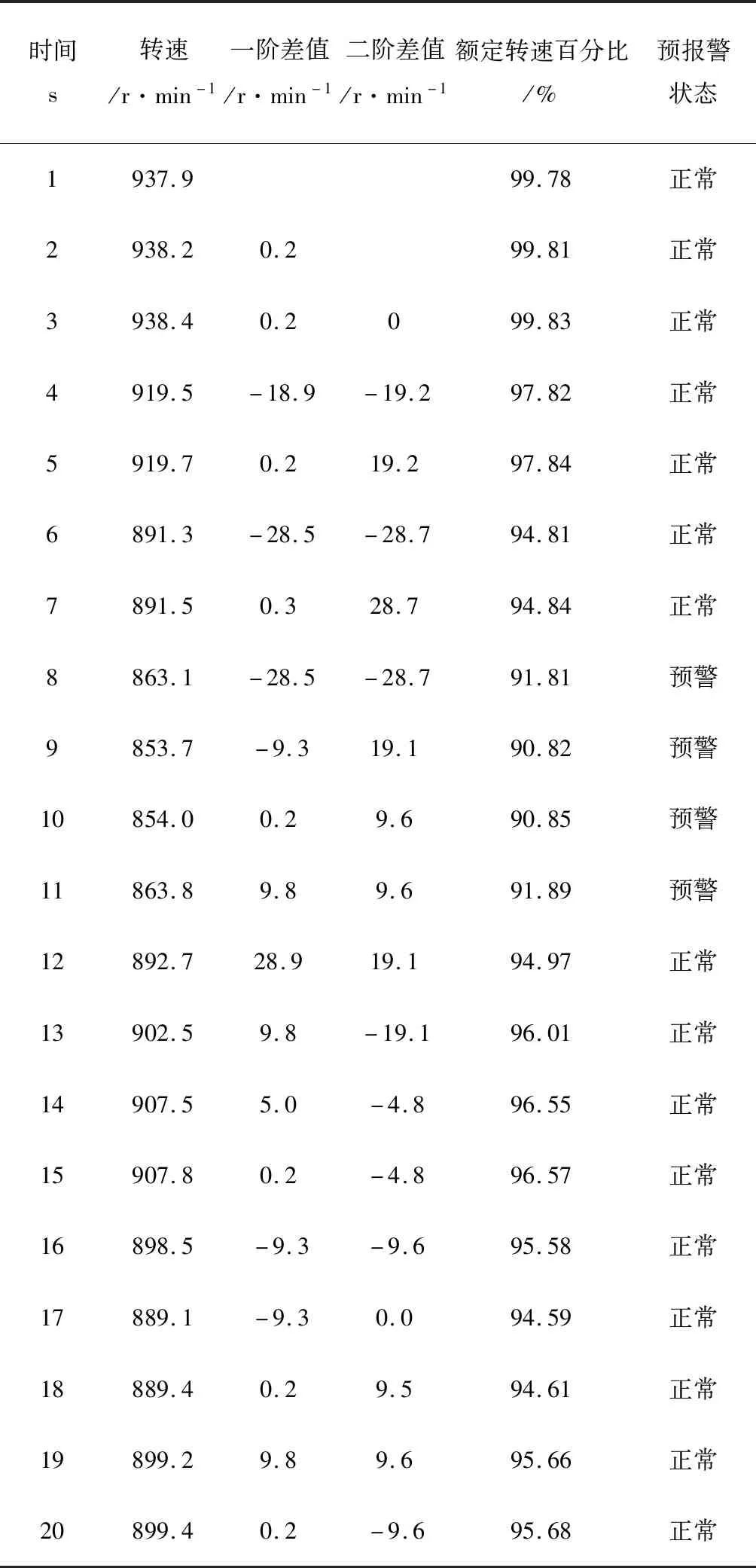
表4 文献[9]中脱粒滚筒转速试验数据Table 4 Test data of threshing cylinder speed in document[9]

对比Simulink仿真模型作业速度输出与文献[9]中的作业速度变化曲线异同,以验证本文所设计的脱粒滚筒转速—期望作业速度模糊控制器与模糊PID作业速度调控算法的正确性。设定转速下降至额定转速的92%时进行预警提示,表4是在额定转速为940r/min时,滚筒转速的预警情况。

以文献[9]中脱粒滚筒田间试验数据为输入在MatLab中建立作业速度调控Simulink仿真模型。该模型分为两个部分,一是脱粒滚筒转速—期望作业速度模糊控制器,二是模糊PID作业速度控制器。仿真模型以脱粒滚筒转速作为脱粒滚筒转速—期望作业速度控制器的输入,根据脱粒滚筒转速变化情况输出期望作业速度给模糊PID作业速度控制器,根据期望作业速度输出伺服阀输入电压,改变伺服阀流量,从而控制液压马达转速,调整作业速度。仿真结果如图3所示。

图3 仿真试验验证Simulink模型Fig.3 Simulation test verifies simulink model

通过图3结合表4可以看出：系统在第8s时脱粒滚筒转速下降至额定转速的91.81%,作业速度下降至1.21m/s,降幅20.9%;随后速度缓慢上升,在第8～11s持续了4s的预警;第12s系统预警消除后,作业速度升至1.61m/s;在第12～20s脱粒滚筒转速正常状态下,系统作业速度保持在1.54～1.63m/s之间,平均速度1.59m/s,波动幅度5.6%,作业速度基本保持稳定。由于系统判定规则的不同,文献[9]中系统在第9s时预警,作业速度开始下降,至第12s时速度由2m/s降至1.6m/s,降幅20%;随着系统预警消除,作业速度随之升至1.8m/s,并保持稳定状态。通过分析仿真模型作业速度输出数据、对比作业速度曲线可以看出：在系统预警时,模糊PID作业速度调控算法可以响应滚筒转速的变化对作业速度进行调整,与文献[9]中作业速度曲线变化趋势基本一致,表明所设计的模糊PID作业速度调控算法可以满足预期要求,验证了模糊PID作业速度调控算法的正确性与可行性。

5 结论

在对4LZZ-1.0小区谷物联合收获机脱粒滚筒堵塞情况和行走系统分析的基础上,确定了调控方案,设计了脱粒滚筒转速—期望作业速度模糊控制器与模糊PID作业速度智能调控算法,并建立了小区谷物联合收获机行走系统数学模型。以大田脱粒滚筒试验数据对调控算法进行了仿真试验验证,结果表明：所设计的调控算法可以根据滚筒转速的变化对作业速度进行调整,与文献[9]中作业速度曲线变化趋势基本一致,作业速度波动幅度5.6%,满足预期要求。