圆形PWM变量喷灌机喷灌特性的仿真研究

周志宇,陶 帅,莫锦秋

(上海交通大学 机械与动力工程学院,上海 200240)

0 引言

变量喷灌(Variable Rate Irrigation ,VRI)指将作业地块分为多个作业管理区,根据各个管理区的土壤墒情、作物长势等决定需水量,再由喷施设备按各管理区需水量作业[1]。

VRI一直是精准农业一个研究热点,已从成熟的SPPED-VRI到进入实际农业应用的ZONE-VRI,目前正向IS-VRI方向展开各类研究。图1为圆形喷灌机上实现这3种VRI时形成的不同管理区划分。SPEED-VRI通过调节喷灌机桁架行进的启停占空比,由实际行进速度实现行进方向上变量喷灌,其管理区呈扇形,如图1(a)所示。ZONE-VRI中桁架上每跨分成几个ZONE(目前产品一般为2个),从而在桁架方向形成多个ZONE。各个出水喷头上设置水阀,同一个ZONE内的水阀由所在ZONE的水阀前级控制环节采用脉宽调制(Pulse Width Modulation, PWM)变量技术统一控制水量。不同的ZONE实现的水量不同,其管理区由图1(b)所示。IS-VRI(Individual Sprinklers VRI)则是每个喷头上的水阀均采用PWM变量技术改变PWM脉冲占空比控制流量。因为每个喷头流量可控制,从而形成更小尺度的管理区,满足更精细的用水需求,如图1(c)所示。

PWM变量技术实施时管路恒压供水,在工作期间各喷头工作压力基本不变,喷头瞬时喷洒特性不变,可确保喷洒的稳定性。KUFAISHI等[2]经过试验对比指出:PWM变量喷灌相比于均一灌溉和部分喷头开启式灌溉,有利于提高灌溉精度和均匀性。PIERCE和AYERS[3]也通过田间试验发现了PWM参数对喷灌精度和均匀性的影响规律。赵伟霞等[4-5]通过实验对比了控制喷灌机行进百分数、控制喷头开启比例和控制PWM占空比3种变量喷灌方法的优劣,并分析了PWM占空比对喷灌效果的影响,提出应在桁架方向相邻管理区设置过渡区以提高喷灌均匀度。张以升等[6]通过实验探究了喷灌机运行速度对喷洒均匀性的影响,并给出了速度与喷灌水深的理论计算公式。O'SHAUGHNESSY等学者[7-10]针对其他影响因素,如风速风向、测点排列、喷头安装高度、喷头间距等,探究了喷头的水量分布及动能分布规律。上述学者的研究中,通常采用一个水阀控制多个喷头,管理区规模较大,水量控制不精细;同时,实验中主要采用雨量筒法,测点少,容易遗漏水量分布信息;且实验周期长,耗费大量人力物力,需要喷灌机的硬件支持,会浪费大量水资源。本文通过分析面向IS-VRI应用的圆形PWM变量喷灌机在喷灌过程中水量累积的特点,在数字空间内模拟仿真喷灌过程,并仿真分析PWM脉冲占空比、PWM脉冲周期、喷灌机行进角速度及喷头离围转中心距离4个参数对喷灌效果的影响,为实际喷灌作业提出指导性建议。

1 圆形PWM变量喷灌机喷灌水深仿真方法

圆形PWM变量喷灌机行进过程中,喷头的喷洒域不断向前扫掠,行进方向上某一点处的喷灌水深是喷头喷洒域不同位置在时间维度上不断累积的结果。喷灌水深与多个因素有关,通常来讲,影响圆形PWM变量喷灌机喷灌水深的主要因素有PWM脉冲占空比、PWM脉冲周期、喷灌机行进角速度及喷头离围转中心距离。

1.1 圆形PWM变量喷灌水量累积过程

为分析水量累积过程,可将作业地块和单喷头喷洒域离散成大小为ΔL·ΔH的单元区域,如图2所示。其中,ORΘ为作业地块极坐标系,orθ为喷头喷洒域极坐标系。喷灌机行进方向上存在相同大小的区域A,当整个喷洒域扫掠过区域A后,喷洒域内对应的区域B1,B2,…,Bn中的水将落入区域A中。 区域B的划分数量n取决于区域A、B在坐标系ORΘ及orθ中的位置。

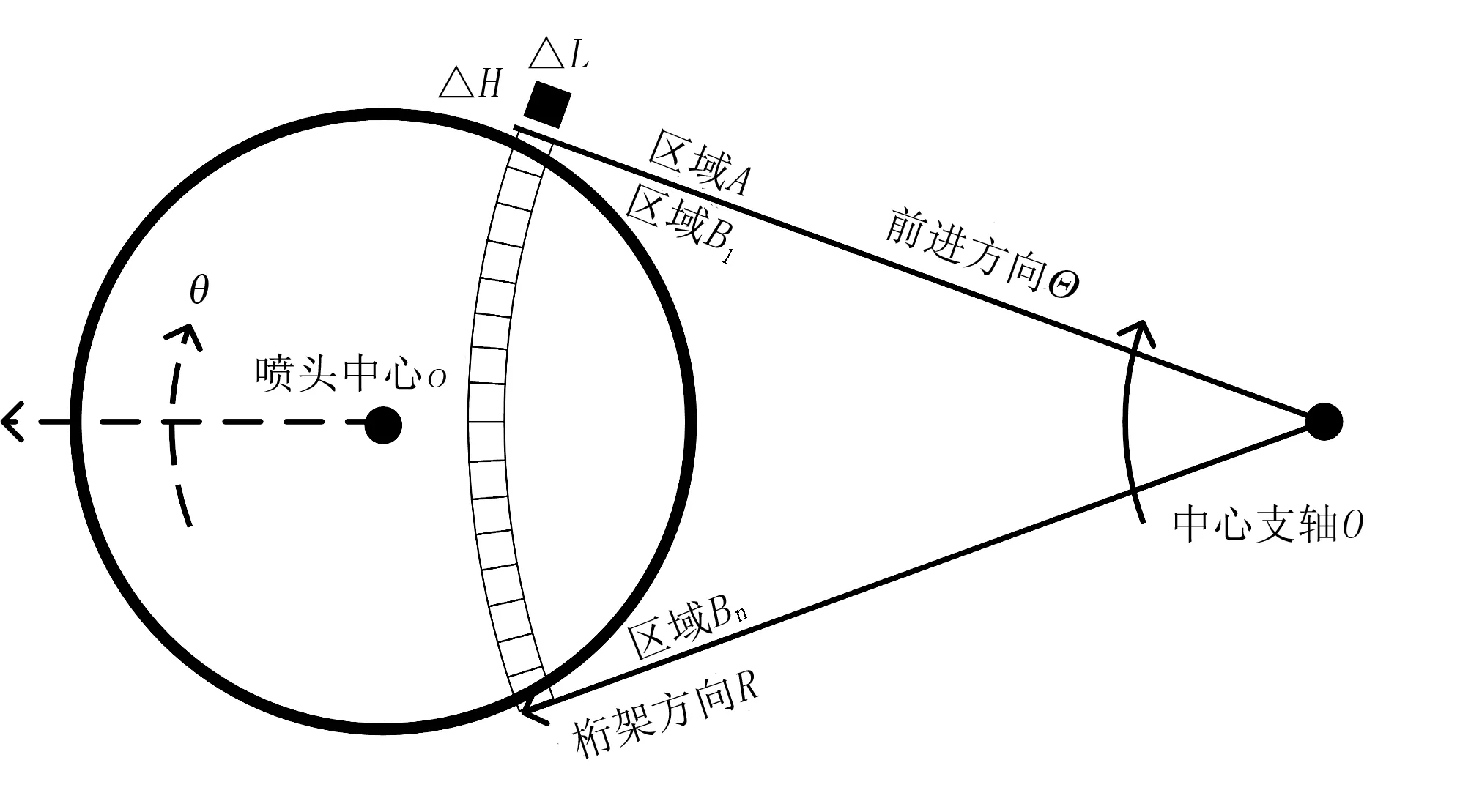
图2 喷洒域及作业地块离散化

不同类型的喷头在不同条件下喷水特性不同,与喷头工作条件如安装高度、工作压力、喷嘴大小有关。采同PWM变量技术后管路恒压供水,已确定安装高度、喷嘴喷头型号的喷头在开启阶段内的喷水特性不变。通常可以采用流量密度ρ来描述单喷头水量分布,即喷洒域内单位面积上在单位时间内的受水量。当喷头为理想的在喷洒域内各处均匀喷洒时,流量密度ρ可以表示为

(1)

其中,ρ为流量密度(mm/h),q为喷头流量(m3/h),R为喷洒域半径(m)。

由于普通喷头无法做到均匀喷洒,流量密度在喷洒域内并不是均布的,它是测点在坐标系orθ中的位置(r,θ)的函数,即

(2)

则区域A中的累积水量为

(3)

其中,ρi为区域Bi(i=1,2,…,n)的流量密度,Δti是区域Bi扫掠过区域A所需的时间。则区域A的累积水深为

(4)

采用PWM脉冲控制喷头喷灌时,区域Bi扫掠过区域A时喷头处于喷水与停喷两种状态之一,可将这种状态定义为

(5)

并将区域A的累积水深修正为

(6)

当ΔL和ΔH足够小时,计量区域A变为点A,即可模拟喷灌机向前连续喷灌,对应地有

(7)

其中,ttotal为喷洒域完全扫掠过点A的时间,θ是圆形喷灌机转过的角度(°)。当喷灌机匀速行进时,有

θ=ωt

(8)

其中,ω为喷灌机行进角速度(°)/min。

1.2 圆形PWM变量喷灌机喷灌水深的仿真流程

圆形PWM变量喷灌机喷灌水深仿真流程,如图3所示。

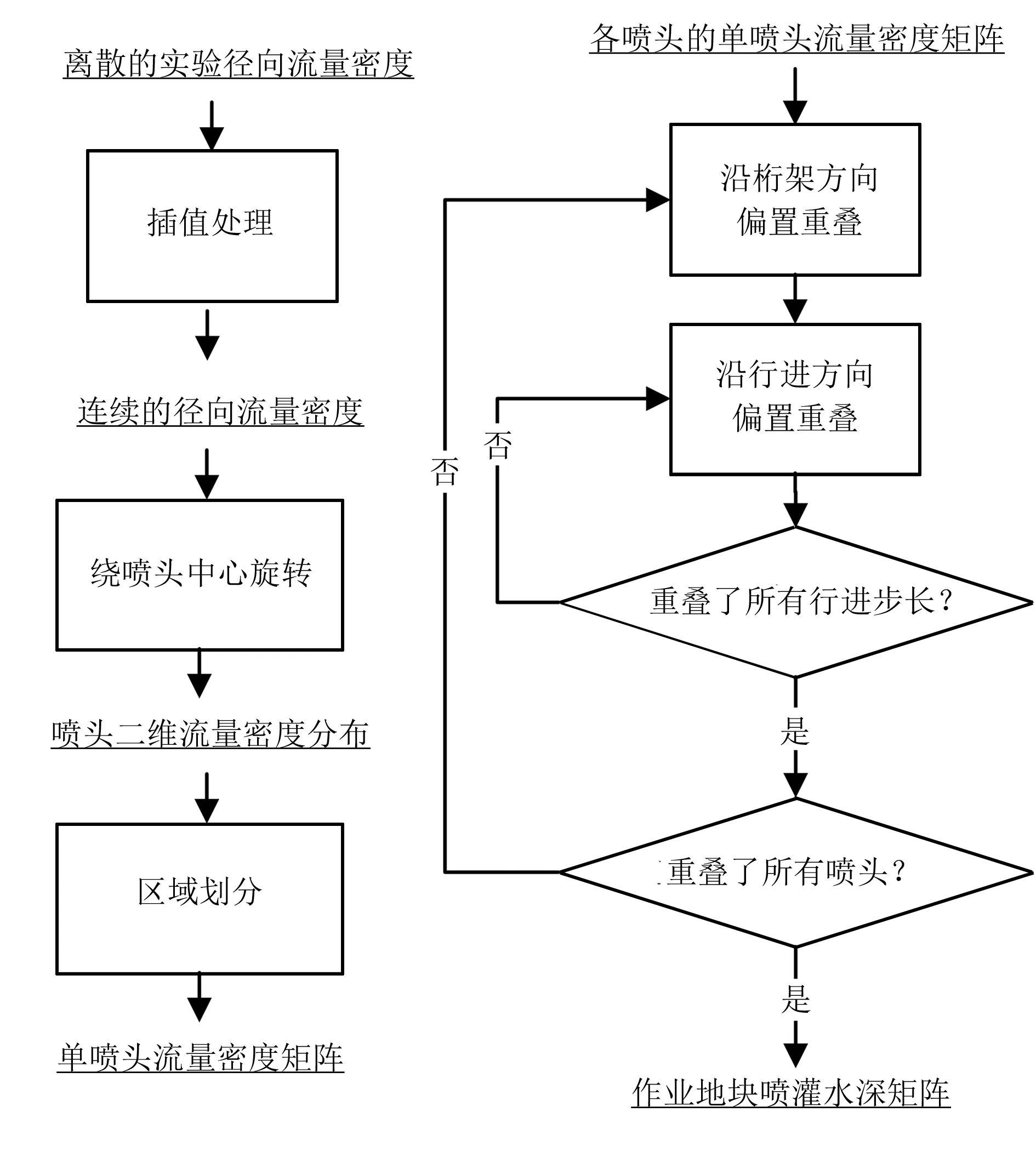
图3 仿真算法流程

由式(7)知:单喷头流量密度是进行圆形变量喷灌机喷灌过程仿真的基础。单喷头流量密度常用的获取方法是雨量筒法测得,在单喷头喷洒域半径方向布置一系列雨量筒,测量一定时间内的积水量,即可得出单喷头径向流量密度分布。将实测数据进行插值处理,得到连续的径向流量密度分布。由于喷头喷洒水量在各个半径方向上是相同的,可将径向流量密度数据绕喷头中心旋转,得到整个喷洒域的二维流量密度分布。水深仿真时将喷头喷洒域划分为ΔL·ΔH大小的单元区域,将各个单元区域内流量密度积分完成喷洒域水量分布离散化。

同样地,将作业地块划分为ΔL·ΔH大小的单元区域,创建相应地块水深矩阵以存储水深累积数据。通过将单喷头流量密度矩阵元素赋值给地块水深矩阵,实现单喷头喷洒过程的模拟;沿桁架方向,以一定的间距将单喷头流量密度矩阵进行偏置,模拟桁架方向多喷头等间距分布;沿前进方向,以足够小的步长将单喷头流量密度矩阵进行偏置,模拟行进方向单喷头连续喷洒。当水阀处于开启状态时,仍需要采用小步长将单喷头流量密度矩阵偏置重叠;水阀处于关闭状态时,偏置步长应为该喷头在这段时间内前进的距离。

2 PWM变量灌溉仿真试验

2.1 仿真试验方法

本文采用MatLab实现上述仿真算法。

采用陈震[11]等在150kPa水压、无风条件下测得的Nelson R3000喷头水量分布数据为单喷头径向流量密度分布数据,喷洒直径为15m。经插值及旋转处理得到单喷头喷洒域二维流量密度分布。

采用以下4个作业变量的不同取值进行仿真,并评估对喷洒结果的影响。

1)PWM脉冲占空比D为10%,20%,…,100%,增量取10%;

2)PWM脉冲周期T为10、20、30、60s;

3)喷灌机行进角速度ω为1、2、3、6°/min;

4)喷头离围转中心距离r为15m,30m,45m,…,150m,增量取15m;

采用的喷洒结果评价指标包括:

1)喷灌水深h。当行进方向上某区域被喷洒域完全扫掠后,各点处的平均水深,单位mm。喷灌水深包括沿桁架方向的平均径向喷灌水深hl和沿行进方向的平均周向喷灌水深hm。

2)喷灌水深误差e。设PWM脉冲占空比为D时平均喷灌水深为hD,PWM脉冲占空比为100%时的平均喷灌水深为h100,则实际的喷灌水深百分比为

(9)

喷灌水深误差可定义为

e=Dsp-D

(10)

喷灌水深误差e包括沿桁架方向的径向喷灌水深误差el和沿前进方向的周向喷灌水深误差em。

3)喷灌均匀性:HANKS等[12]通过实验发现,当喷头间距设置为喷洒域直径的20%～25%时,喷灌均匀性较好。实验中采用的Nelson R3000喷头喷洒直径为15m,故喷头间距设置为直径的25%,即3.75m。如图4所示:4个喷头的喷洒区域相互重叠,并在中间形成一个4喷头重叠区域,该区域喷灌水深由4个喷头流量共同决定,可将其作为一个管理区。喷灌均匀性通常采用克里斯琴森均匀系数Cu作为评价指标[13-16]。本文将考查沿桁架方向的径向均匀性系数Cul和沿行进方向上的周向均匀性系数Cum。

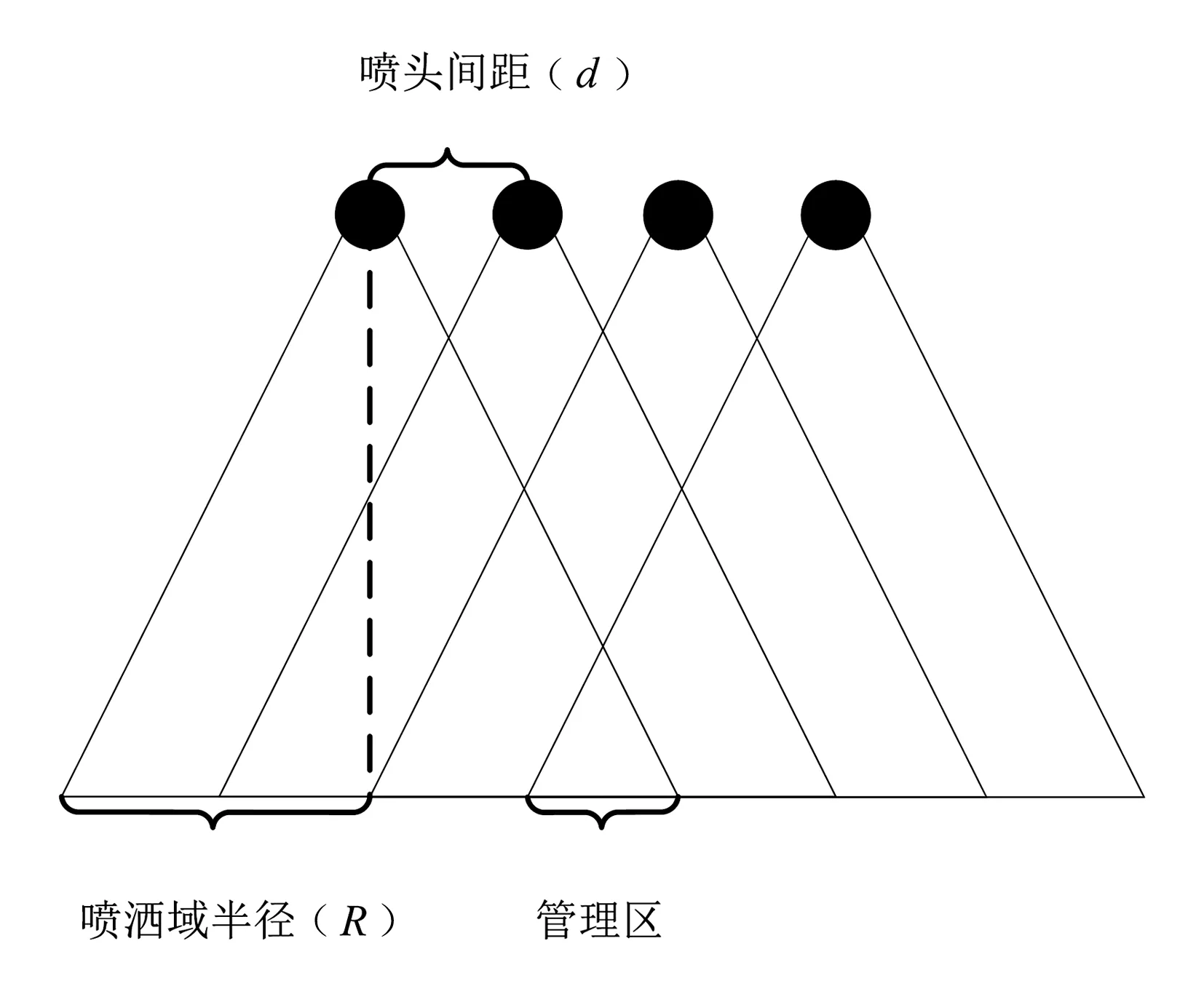
图4 喷洒域叠加示意图

2.2 试验结果及讨论

2.2.1 PWM周期对喷灌结果的影响

设置喷灌机行进角速度为6°/min,喷头离围转中心距离分别为30m及150m(简称为近端及远端),分别仿真计算不同PWM周期下喷灌均匀性、水深、水深误差e随PWM脉冲占空比变化的情况。

图5所示为不同PWM周期下喷灌均匀性随PWM脉冲占空比的变化。整体来讲,PWM周期越大,均匀性越差。当周期取10s时,远、近端的Cul和Cum均可达到75%和80%以上。PWM周期对周向均匀性影响大于对径向均匀性影响,当PWM周期过大时,Cum可能为负数。Cum波动范围比Cul大,Cum最大值可以达到90%以上,远好于Cul;Cum最小值可为负数,远小于Cul。

在远离围转中心处,PWM周期过大会导致均匀性骤降,即PWM周期对远端均匀性影响大于对近端均匀性的影响,同样条件下,近端均匀性更好。

(a) 远端径向均匀性Cul (b) 近端径向均匀性Cul

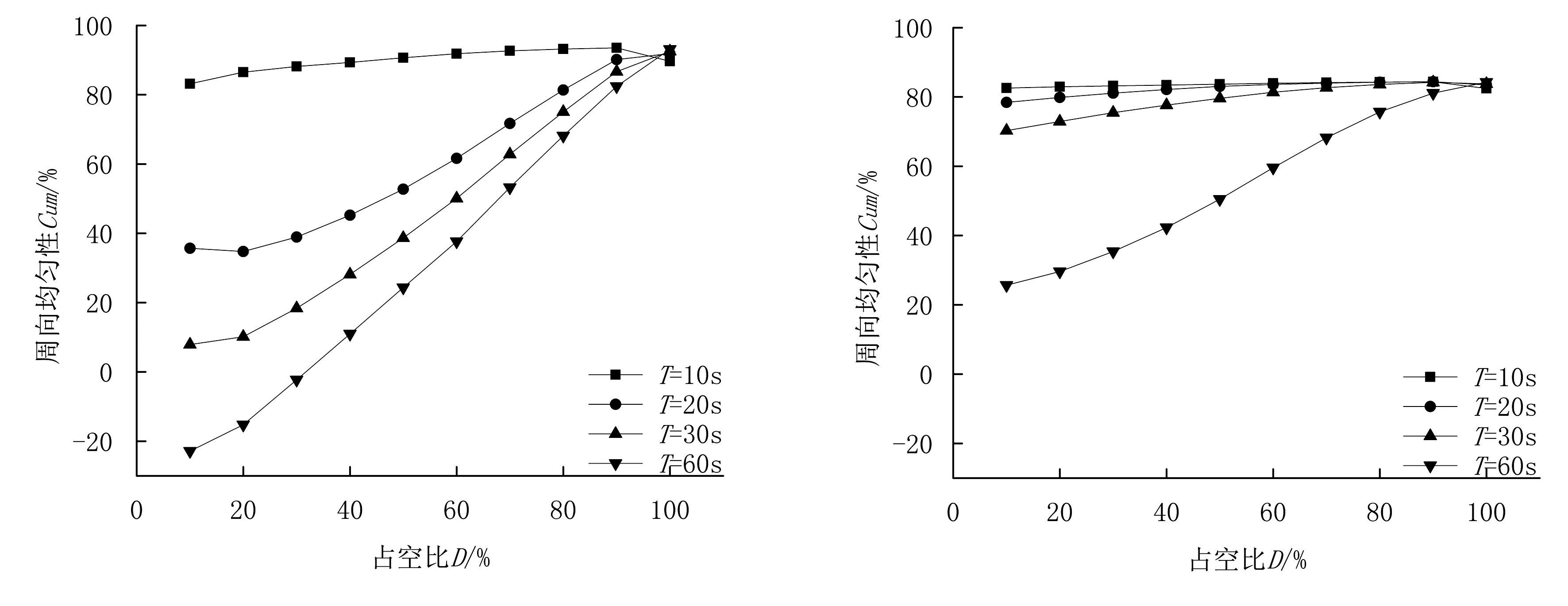
(c) 远端周向均匀性Cum (d) 近端周向均匀性Cum

图6所示为不同PWM周期下喷灌水深随PWM脉冲占空比变化的情况。由图6可知:周向水深比例性优于径向,近端水深比例性优于远端;水深变化曲线的斜率,尤其是周向水深变化曲线的斜率,随PWM周期变化不大;水深变化曲线的截距随PWM周期增大而减小,说明水深与PWM周期存在较弱的负相关关系。

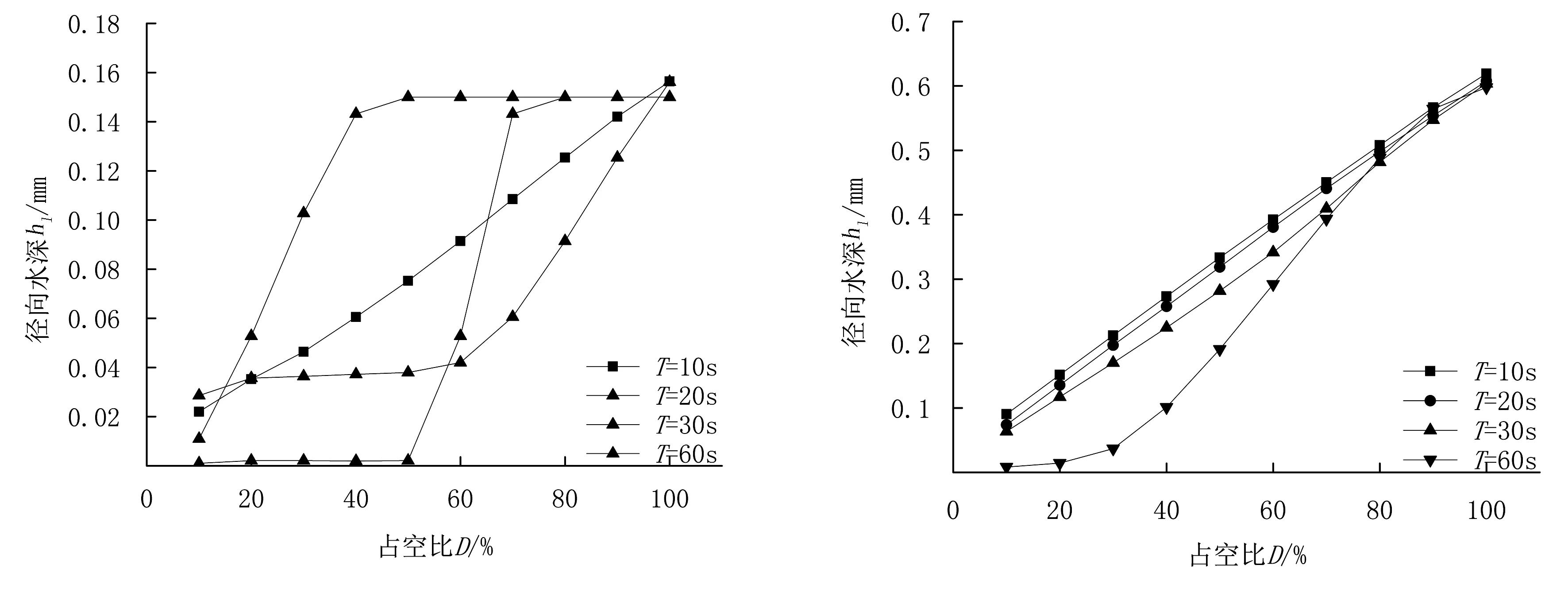
(a) 远端径向水深hl (b) 近端径向水深hl

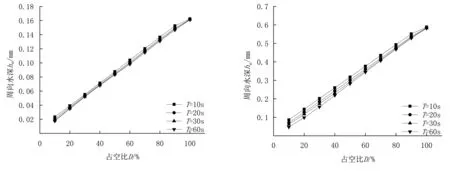
(c) 远端周向水深hm (d) 近端周向水深hm

图7进一步给出不同PWM周期下水深误差e随PWM脉冲占空比变化的情况。由图7可以发现:远端处PWM周期越小径向水深误差el越小;近端在PWM周期10～30s范围内随PWM周期减小径向水深误差el反而增大,但PWM周期很大时,径向水深误差el却会大幅增大。远近端PWM周期越小,周向误差反而越大。此外,PWM周期对径向水深误差el影响大于对周向水深误差em影响,对远端水深误差e影响大于对近端水深误差e影响。鉴于此,选取PWM周期时优先选择能使远端径向水深误差el更小的PWM周期值。当然,在水深误差e随PWM脉冲占空比变化比较平稳时,可以采用占空比补偿法减小水深误差e。以喷头离围转中心距离150m、PWM周期为10s时为例,此时在不同PWM脉冲占空比时水深误差e基本稳定在4%,因此若设计的灌溉水深为最大灌溉水深的p%时,应将PWM脉冲占空比设置为(p-4)%。

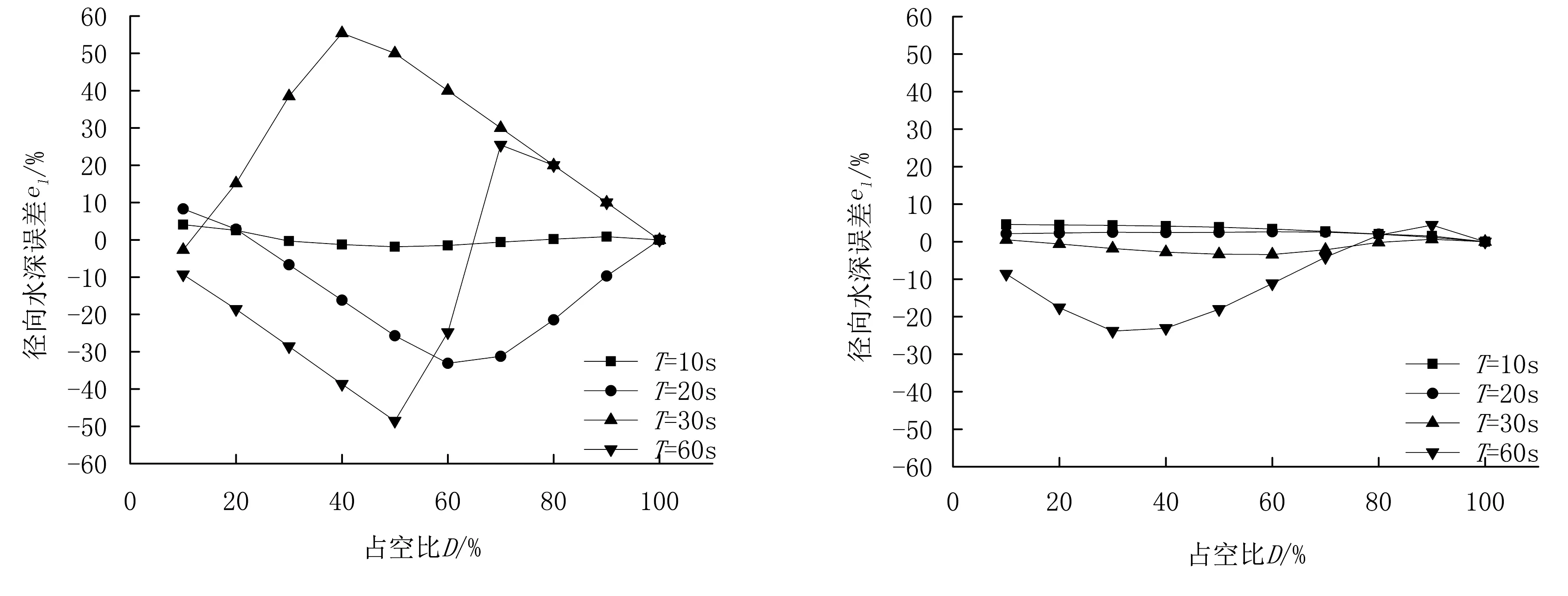
(a) 远端径向水深误差el (b) 近端径向水深误差el

(c) 远端周向水深误差em (d) 近端周向水深误差em

2.2.2 喷灌机行进角速度对喷灌结果的影响

设置PWM脉冲周期为60s,喷头离围转中心距离分别为30m及150m(简称为近端及远端),分别仿真计算不同喷灌机行进角速度下喷灌均匀性、水深、水深误差e随PWM脉冲占空比变化的情况,得到如图8～图10所示结果。

对比图5和图8、图7和图10可知:行进角速度对喷灌均匀性及水深误差e的影响与PWM周期的影响类似,二者不同之处在于与喷灌水深的比例特性参数的影响不同。对比图6和图9可以发现:与PWM周期的影响类似,周向水深比例性优于径向,近端水深比例性优于远端,但曲线斜率与行进角速度有明显的负相关关系。

(a) 远端径向均匀性Cul (b) 近端径向均匀性Cul

(c) 远端周向均匀性Cum (d) 近端周向均匀性Cum

(c) 远端周向水深hm (d) 近端周向水深hm

(a) 远端径向水深误差el (b) 近端径向水深误差el

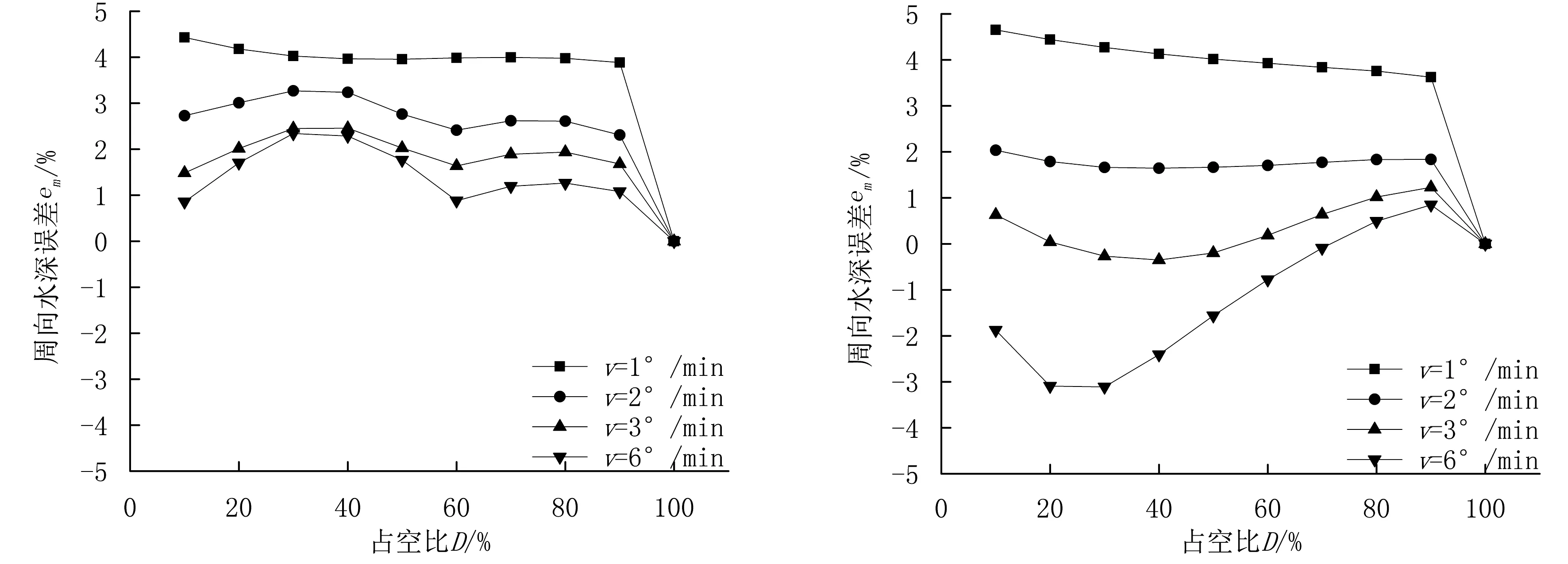
(c) 远端周向水深误差em (d) 近端周向水深误差em

将图9中的曲线做线性拟合h=aD+b,再将曲线斜率与行进角速度做幂拟合a=dωc,结果如表1所示,可知幂次接近于-1,这说明喷灌水深与行进角速度近似呈反比关系。

表1 喷灌水深与行进角速度关系曲线的拟合结果

2.2.3 喷头离围转中心距离对喷灌结果的影响

由上两节可知,PWM周期、行进角速度取较小值有利于提高喷灌均匀性。取PWM周期为10s、行进角速度为1°/min,分别仿真当喷头距围转中心距离及PWM脉冲占空比发生变化时,喷灌均匀性、水深、水深误差变化规律,得到如图11和图12所示结果。

由图11可知:径向均匀性随着喷头离围转中心距离增大而减小,而周向均匀性随喷头离围转中心距离增大而增大。由于周向均匀性变化幅度大于径向均匀性,应用时可以牺牲一定的径向均匀性来改善周向均匀性。结合上两节的结论,在离围转中心较近的一端,应设定较小的周期,保证近端周向均匀性;在离围转中心较远一端,可以设定相对较大的周期,防止水阀动作过快导致比例特性不佳。

(a) 径向均匀性Cul (b) 周向均匀性Cum

(a) 径向水深hl (b) 周向水深hm

(c) 径向水深误差el (d) 周向水深误差em

图12(a)、(b)表明:喷头离围转中心不同距离处的喷灌水深的比例特性均较好,而斜率与喷头离围转中心距离呈负相关关系。将其中的曲线做线性拟合h=aD+b,再将斜率与喷头离围转中心距离做幂拟合a=dωc,结果如表2所示。由表2可知:幂次接近于-1,说明喷灌水深与喷头离围转中心距离近似呈反比关系。

表2 喷灌水深与喷头离围转中心距离关系曲线的拟合结果

对比图12(c)、(d)可以发现:对于径向水深误差el,喷灌机中间位置误差较大,可到8%左右,两端误差较小,在5%以下;对于周向水深误差em,喷灌机近端误差较大,远端误差较小;而周向水深误差em整体小于径向水深误差el,在5%以下。因此,占空比补偿法可以主要应用在喷灌机中间段,用以减小其径向水深误差el。

3 结论

1)喷灌水深与喷灌机行进角速度和喷头离围转中心距离成反比,与PWM周期存在较弱的负相关关系。灌溉水深与PWM脉冲占空比成正比,比例特性的强弱与喷灌机行进角速度和PWM周期取值有关,当二者较小时,比例性更明显。

2)整体来讲,PWM周期和喷灌机行进角速度越小,喷灌均匀性越好。当PWM周期取10s或喷灌机行进角速度取1°/min时,远近端的径向和周向克里斯琴森均匀系数均可达到75%和80%以上。此时,喷灌机近端和远端周向均匀性差异较大,远端周向均匀性好,近端周向均匀性差。因此,可以考虑近端设置较小的周期,远端可以维持较大的周期,保证水阀比例特性良好。

3)PWM周期和喷灌机行进角速度越小,远端径向水深误差el越小,近端径向水深误差el越大。但PWM周期和行进角速度过大时,近端径向水深误差el同样会急剧增大。远近端周向水深误差em均随周期和行进角速度减小而增大。虽然灌溉误差变化规律与均匀性变化规律相反,但灌溉误差随PWM脉冲占空比变化幅度不大,可采用补偿法消除误差。另外,喷灌机径向水深误差el要大于周向水深误差em,且最大值出现在喷灌机中间段,约为8%,其余位置误差在5%以下,因此补偿法可以考虑仅应用在中间段的喷头上。