基于贝叶斯网络分类算法的采摘机器人故障诊断研究

李卓然

(罗定职业技术学院 电子信息系,广东 罗定 527200)

0 引言

随着科学技术的发展,采摘机器人在水果、蔬菜等采摘方面取得了广泛的应用。由于采摘机器人工作环境复杂、零部件众多,故障率也较高,而一旦其发生故障,会对用户、工作空间和采摘对象造成伤害。因此,实现对采摘机器人的故障诊断,一直是一个非常重要的研究领域。本文研究的基于贝叶斯网络分类算法的采摘机器人故障诊断,将贝叶斯网络和故障特征分析结合起来,能够实现采摘机器人动力故障和执行器的故障诊断。

1 贝叶斯网络分类算法

贝叶斯网络是基于概率理论的统计模型,是一种非常重要的定量模型求解方法,具有丰富逻辑理论和数学模型。

1.1 贝叶斯定理

1)条件概率理论:假设存在A、B两个独立的事件,其中A事件发生的概率大于0,则

(1)

其中,P(B|A)为A事件发生的基础上B也同时发生的概率。

2)联合概率理论:假设存在A、B两个独立的事件,其中A事件发生的概率大于0,则两个事件的联合概率为

P(A·B)=P(A)P(A|B)

(2)

其中,P(A·B)为两个事件同时发生时的概率。

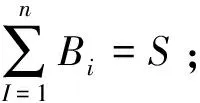
(3)

4)贝叶斯分类理论:根据前面介绍的3种概率公式,可以推导出贝叶斯分类计算公式,即

(4)

以上公式是贝叶斯分类的基础。

1.2 贝叶斯网络分类

1)贝叶斯网络分类概述。采摘机器人故障诊断的基础是建立从故障征兆到故障特征的映射关系,其理论基础是根据故障征兆变量确定故障类型。贝叶斯网络分类算法是一种典型的统计学分析方法,根据贝叶斯理论,研究故障发生的先验概率与后验概率结合起来,根据先验概率和样本集求出后验概率值。

假设U={X1,X2,…,Xn,C}为离散变量的集合,Xi为属性变量,C为类变量集合,xi是Xi的取值。实例Ii=(x1,x2,…,xn)为类cj的概率,可以用贝叶斯公式表示为

(5)

其中,P(cj)为cj的先验概率,P(ci|x1,x2,…,xn)为cj的后验概率。式(5)可以改写为

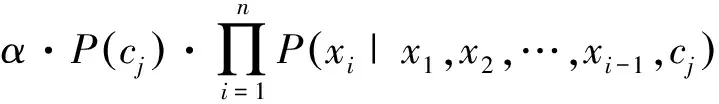
(6)

其中,α为正则参数。从式(6)可以看出:贝叶斯算法选择P(ci|x1,x2,…,xn)最大的类cj为Ii的类标签,因此贝叶斯算法的核心是求解P(ci|x1,x2,…,xn)的值。

本文将介绍朴素(NaiveBayes,NB)和TAN(Tree Augmenetd Naive Bayesian,ATN)两种贝叶斯分类方法。

2)NB贝叶斯网络分类器。NB贝叶斯网络分类器的原理是设定其变量条件之间相互独立,每个属性只和类变量C关联,这一条件极大程度地降低了贝叶斯算法的复杂度,其计算公式可以表示为

(7)

虽然存在着一个变量相互独立的假设,但是NB贝叶斯网络分类器仍具有相当高的健壮性和有效性,分类精度也非常高。NB贝叶斯网络分类器模型如图1所示。

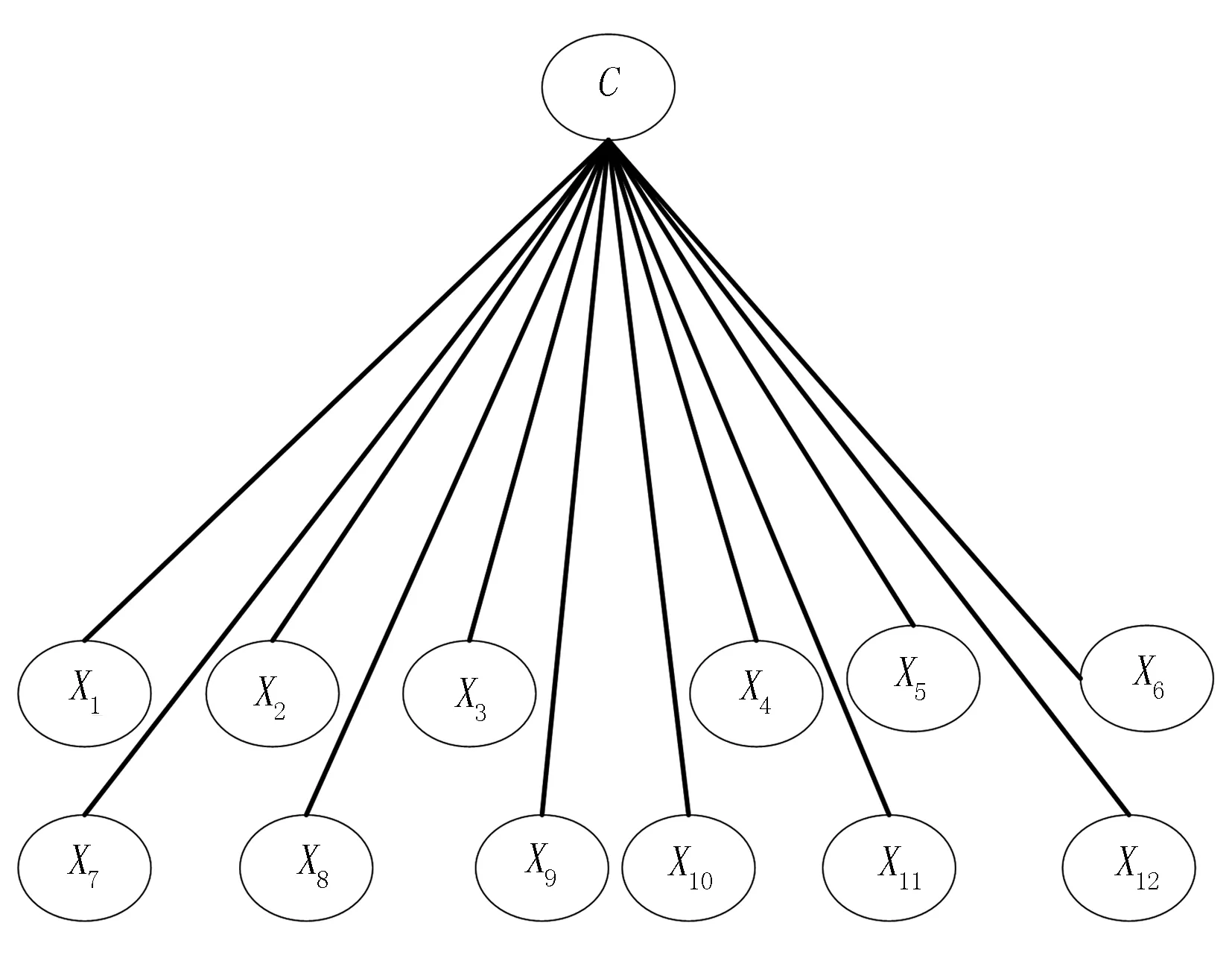
图1 NB贝叶斯网络分类器模型

3)TAN贝叶斯网络分类器。TAN贝叶斯网络分类器是针对NB模型的进一步优化改进,其假设变量之间符合树状结构,而不要求变量条件之间相互独立,允许多个节点变量同时依赖一个节点变量,满足学习速度和精度之间的一种平衡,其计算公式可以表示为

(8)

其中,Pαi为xi的父节点,分为类节点与属性变量等两类。

TAN贝叶斯网络分类器也同样具有高效性和较高的分类精度,模型如图2所示。

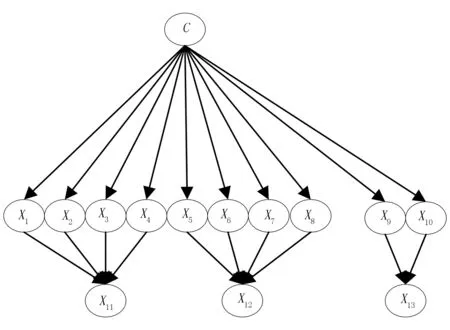
图2 TAN贝叶斯网络分类器模型

2 采摘机器人故障诊断贝叶斯网络模型

2.1 采摘机器人故障诊断节点的选取

采摘机器人是一个零部件多、机械结构复杂的系统,由行走机构、电机驱动、末端执行器、传感器结构、控制器和机器人本体构成。行走机构为采摘机器人提供行进动力;电机驱动用来控制采摘机器人的前进、后退、转弯及采摘手臂的姿态控制等;末端执行器用于采摘目标水果,传感器结构用于获取采摘机器人采摘手臂的姿态信息。采摘机器人结构如图3所示。

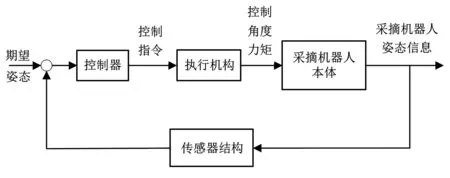
图3 采摘机器人结构示意图

采摘机器人行走机构包括转向轮、推力器,以及传感器结构位置、力度和角度等姿态传感器;末端执行器是采摘机器人之重要部件,采摘机器人能够完成采摘任务主要依靠末端执行器,因此末端执行器的故障会影响整个系统的性能。

综上,本文选取转向轮、推力器、位置传感器、力度传感器、角度传感器和末端执行器为故障诊断参数。

在实际的故障分析中,采集到的数据都是连续的,先需要进行数据离散处理,然后利用贝叶斯网络分类器进行分析。本文研究的故障诊断参数离散化如表1所示。

从表1可以看出:故障诊断参数分为正常、故障和严重故障3个等级, “正常”表示采摘机器人运行正常,“故障”表示采摘机器人运行寿命缩短,“严重故障”表示采摘机器人功能将异常或完全失效。

表1 采摘机器人故障诊断参数离散化

2.2 建立采摘机器人故障诊断贝叶斯网络模型

为了实现对采摘机器人故障进行分析和诊断,本节在上一节的基础上,建立采摘机器人故障诊断贝叶斯网络模型。根据采摘机器人运动控制、末端执行器执行原理,可以分层建立采摘机器人故障诊断贝叶斯网络的拓扑图。第一步,建立贝叶斯网络的根节点,即为转向轮、推力器、位置传感器、力度传感器、角度传感器和末端执行器等6个节点;第二步,通过逻辑分析,确定以上6个节点和行走机构、传感器结构、末端执行器之间的连接方向。本文建立的采摘机器人故障诊断贝叶斯网络模型如图4所示。

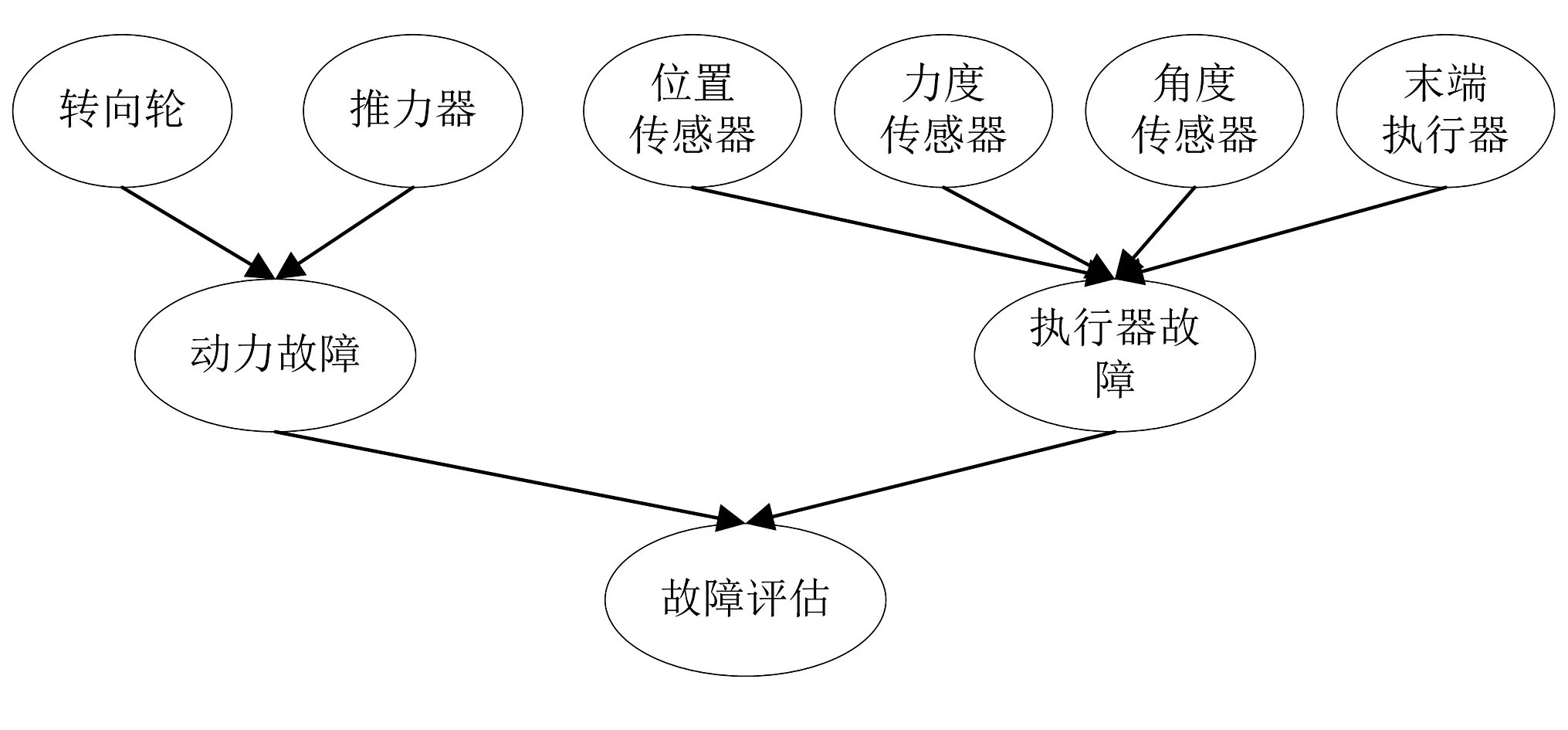
图4 采摘机器人故障诊断贝叶斯网络模型

2.3 确定贝叶斯网络节点参数

确定贝叶斯网络节点参数的实质是确定节点的条件概率分布,但在这之前需要提前确定节点的验前分布。在实际研究中,一般会假设系统参数的验前分布状态是已知条件。本文取Beta(p,a,b)分布作为采摘机器人故障诊断贝叶斯网络中节点的验前分布,具体的验前分布信息如下:

1)节点p的均值P0条件已知,则

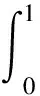
(9)

2)验前分布节点参数a、b或者p的最小值已知,则

a≥a-,b≥b-或p≥p-

(10)

3)点参数p的置信区间[p1,p2]已知,则

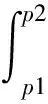
(11)

假设P0条件已知,可以根据验前概率密度获取a和b,即

(12)

确定节点的条件概率分布主要是计算参数a、b的最优值及π(p)的熵,则

H(Beta(p,a,b))=HB(a,b)=

(13)

假设P0已知,则联立式(9)和式(13)可得

a/(a+b)=p0

(14)

因此,可以将a*、b*最优求解问题转换成多个约束条件下求极值的问题,则

(15)

利用式(15)可以求出节点参数验前分布的概率分布参数,通过SOC神经网络算法进行训练后,即能够为采摘机器人故障诊断提供依据。

3 实验与分析

采用TAN贝叶斯网络分类器模型和SOC神经网络结合的方式对采摘机器人特征参数进行故障诊断分析。

3.1 SOC神经网络方法

SOC神经网络是一种无监督的网络算法,其可以对输入的数据参数进行聚类分析。SOM神经网络整体架构如图5所示。

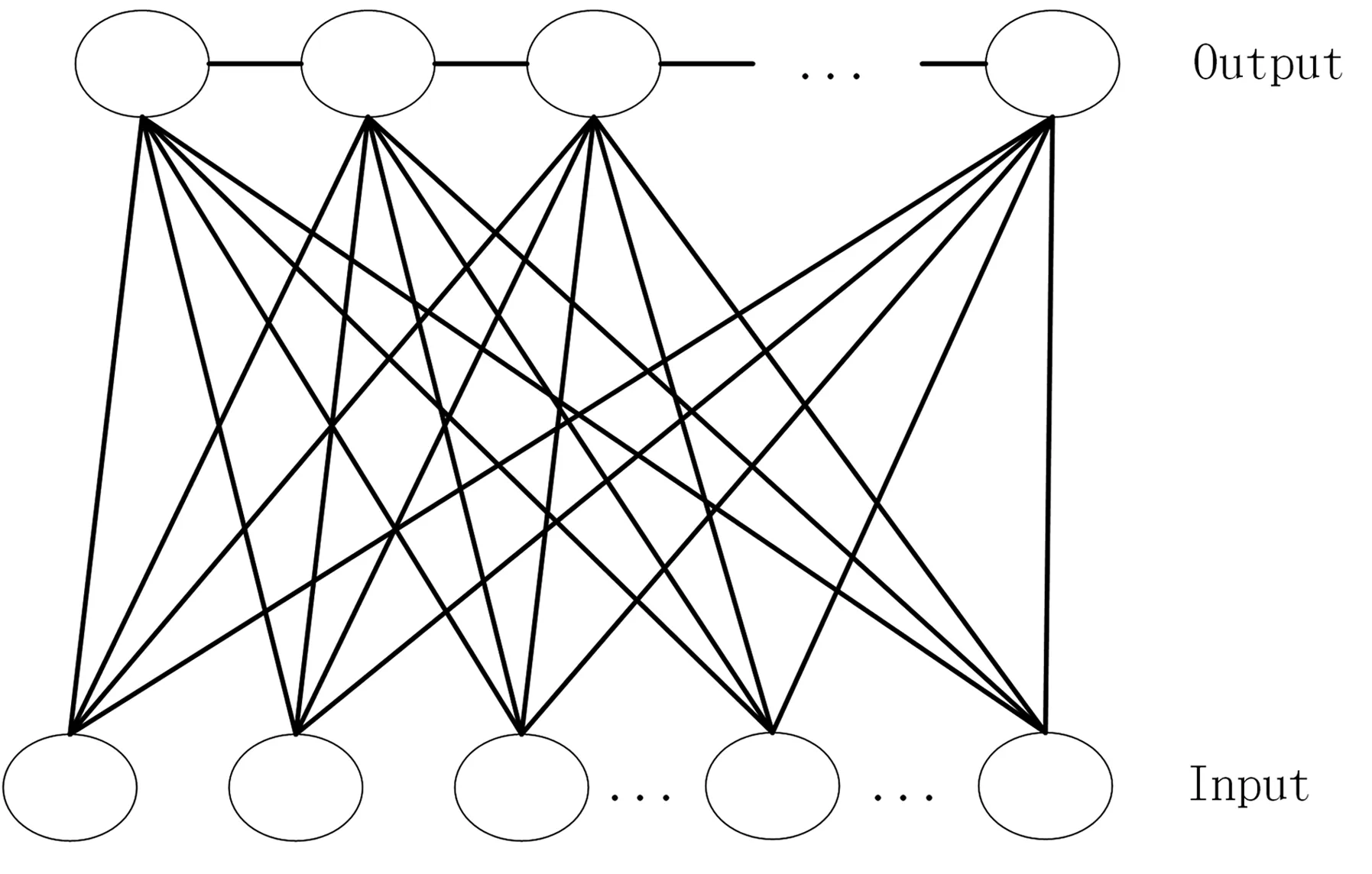
图5 SOM神经网络整体架构

SOM神经网络实现的流程主要有:

1)设置初始权值。SOM神经网络的初始权值为Wi,j(t)为a,介于0～1之间,同时设置算法的初始领域N(0),学习率为η(t),迭代次数为T。

2)选出输入神经元。在采集到参数节点的数据中选出一组Xk作为输入的初始神经元,即

(16)

3)计算欧式距离。利用SOC神经网络算法,计算出Xk与各个神经层之间的欧式距离dj,k,即

(17)

其中,j为神经元个数。

4)求出最优的神经元,即

dj,k=min(d1,k,d2,k,…,dp,k)

(18)

5)修正权值W为

Wi,j(t+1)=Wi,j(t)+η(t)hb,j(t)[Xi(t)-Wi,j(t)]

(19)

(20)

其中,b为最优领域节点,rb、rj为输出节点在点b、j的位置。

一直重复步骤1)～步骤5),直到t从0到T。

3.2 诊断结果分析

为验证本文设计的基于贝叶斯网络分类算法的采摘机器人故障诊断系统设计的可行性和可靠性,利用上诉诊断流程,对NB和TAN2种贝叶斯分类方法进行了对比分析,故障诊断结果如表2所示。

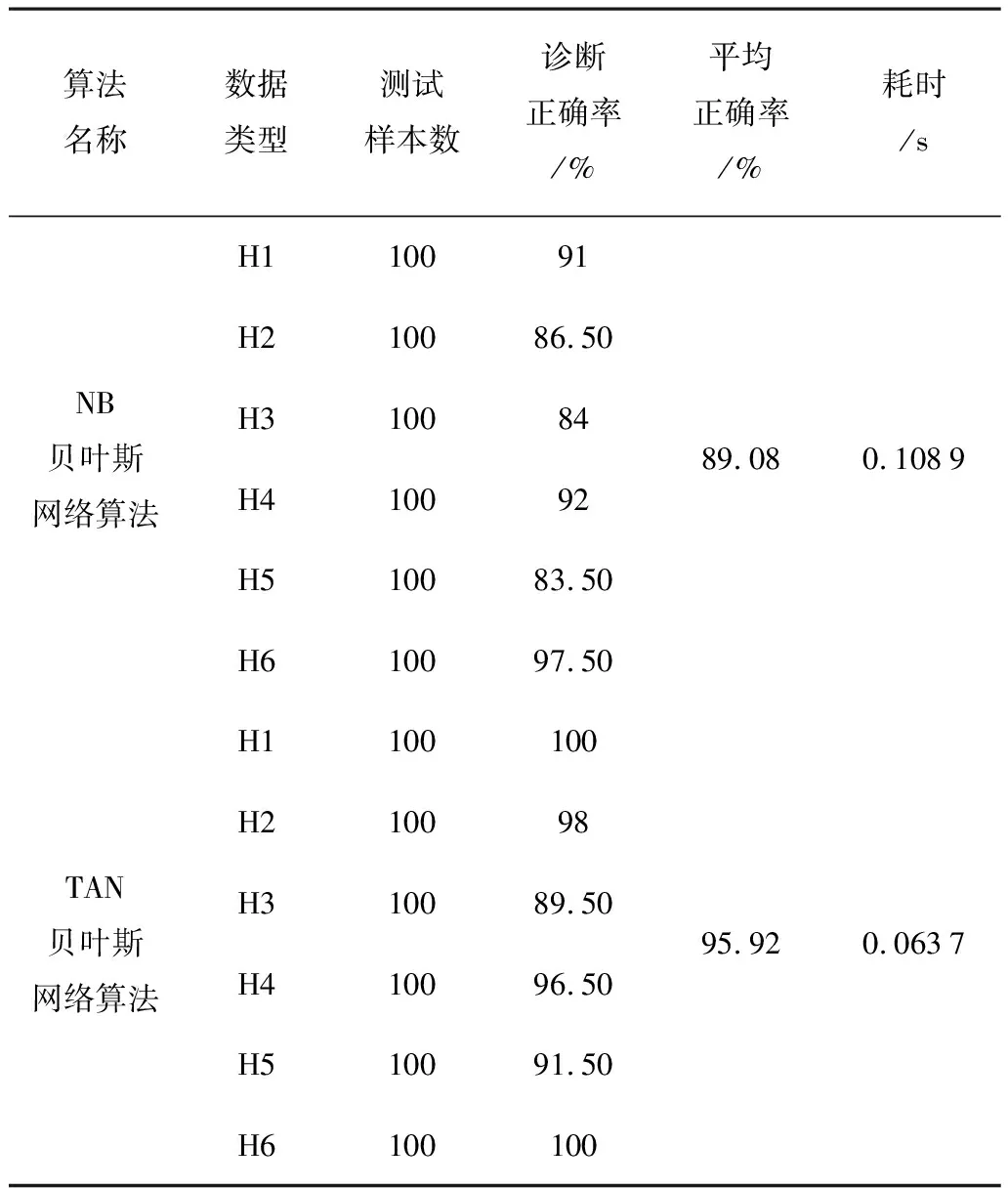
表2 采摘机器人故障诊断结果对比

由表2可以看出:无论从故障诊断平均正确率还是耗时时间,TAN贝叶斯网络算法相比于NB算法都有很大的提高;在故障诊断正确率方面,TAN贝叶斯网络算法高达95.92%,比NB贝叶斯网络算法高了近7个百分点;在耗时时间方面,TAN贝叶斯网络算法仅需要0.063 7s,比NB贝叶斯网络算法缩短近40ms。因此,基于贝叶斯网络分类算法的采摘机器人故障诊断系统,不仅适用于采摘机器人动力故障,对执行器故障也具有相同效果,且能较大地提高故障诊断正确率和效率。

4 结论

针对贝叶斯网络算法进行了介绍和研究,并在此基础上建立了采摘机器人故障诊断贝叶斯网络模型,能够实现采摘机器人的动力故障和执行器故障的诊断检测。实验结果表明:在故障诊断正确率方面,TAN贝叶斯网络算法比NB算法高了近7个百分点;在耗时时间方面,TAN贝叶斯网络算法NB算法缩短近40ms,说明该系统不仅适用于采摘机器人动力故障和执行器故障诊断,且能够较大的提高故障诊断正确率和效率。