基于扩展度动态测量的水泥浆体流变参数表征
伍勇华,党梓轩,祝 婷,李 莹,何 娟
(西安建筑科技大学材料科学与工程学院,西安 710055)
0 引 言
混凝土的坍落度试验、坍落扩展度试验以及水泥净浆的扩展度试验是评价水泥基材料流动性最常用的试验方法。然而无论是坍落度或坍落扩展度,都只是人为定义的一个经验值,对于描述水泥基材料的流变行为仅能提供参考性指标,无法量化表征浆体的流变参数。水泥浆体是典型的非牛顿流体,一般认为水泥基材料(尤其在水泥浆较稀或剪切速率较低时)浆体的流动符合Bingham模型[1-2],可采用流变仪获得水泥基材料的流变参数。但由于流变仪价格昂贵,不适合现场快速测定水泥基材料流变性能,因而有学者致力于通过简单的现场测试来评价水泥基材料的流变参数[3-6]。水泥净浆扩展度试验中浆体的流动过程依赖于浆体的塑性粘度和屈服应力这两个关键的流变学参数,水泥浆体的流变行为是流变参数的宏观表现[7]。
本文针对较稀的水泥浆体,借鉴已有坍落度试验相关理论,建立数学模型,利用扩展度动态测量,对水泥浆体的屈服应力和塑性粘度进行表征,并与流变仪测定值进行比较,以期获得利用动态测量水泥浆体扩展度评价水泥浆体塑性粘度和屈服应力的方法。
1 动态测量表征浆体流变参数模型的建立
1.1 坍落扩展侧面滑移模型
很多研究者在对混凝土坍落度实验分析后认为,混凝土坍落时,截锥体拌合物在自重作用下变形,截锥体自上而下,水平剪切应力逐渐增大,只有下部剪切应力τx大于屈服应力的部分发生流动变形[8-9],如图1所示。h0为未变形区域混凝土高度,h1为已变形区域混凝土高度,S为混凝土坍落度。

图1 混凝土坍落截锥体的变形[9]Fig.1 Deformation of the concrete collapse dome[9]
在扩展度较大的水泥浆体中,由于其屈服应力很小,因此截锥形浆体在整个高度上发生流动变形。已有的模型通常将截锥体分割成水平层,研究每个水平层的流动特点。但实际大流动度浆体的流动,在扩展初期是截锥体侧表面的不断滑移形成层流产生的,因此可以采用侧面滑移模型对浆体流变行为进行分析,如图2所示。为简化计算,可做如下设定:(1)截锥体上表面由于不受外力作用,因此在坍落过程中形状保持不变(即上底半径r不变),只是高度不断降低(这一点可以通过上表面着色方法证实);(2)浆体侧表面斜面的剪切应力为垂直应力与水平应力的合力;(3)截锥体下底圆心在坍落过程中位置始终不变,因此该点浆体剪切速率为0;(4)浆体的坍落过程可以看作是以截锥体下底圆心为中心,截锥体侧面不断侧向滑移形成的,在扩展初期的匀速扩展阶段,其最底层外沿(图2中D′点)的名义剪切速率(垂直于流动方向的速度梯度)可以由斜面边长Li的变化速率(名义流动速度)与其到下底圆心的垂直距离(图2中hi)之比表征。

图2 侧面滑移坍落模型Fig.2 Side slip slump model
1.2 侧面滑移模型中剪切应力的表征
Murata等[9-11]根据力的平衡关系,推导出截锥形浆体中距顶部距离为d的任一水平层浆体受到的垂直方向应力τy为:
(1)
式中:ρ为浆体容重;g为重力加速度;Vd为d层以上浆体体积;rd为该层浆体的半径。
侧面滑移模型中的剪切应力如图3所示,设截锥体侧面与竖直方向夹角为α,该夹角随着坍落过程不断增大,则任意层浆体斜边处的剪切应力τz可以表示为:

图3 侧面滑移模型中的剪切应力Fig.3 Shear stress in side slip slump model
(2)
结合式(1)和式(2)可得任意层浆体沿侧面z方向上受到的剪切应力τz为:
(3)
因此,在侧面滑移模型中,假定浆体体积不可压缩,则坍落时任意时刻最底层浆体外沿(图2中D′点)沿侧面z方向上受到的剪切应力可以表示为:
(4)
式中:V为坍落度筒容积;xi为底面扩展半径;αi为任意时刻截锥体侧面与竖直方向的夹角。
根据图2,由几何关系可得:
(5)
(6)
(7)
1.3 侧面滑移模型中名义剪切速率的表征
由于截锥体试模的阻挡,对截锥高度进行动态测量的起始段无法获得,而截锥体下底面半径xi可以通过动态测量获得较精确的值。因此,可以对不同时刻下底面半径xi进行动态测量,再结合上述模型假设,依据式(7)计算出不同时刻的斜边长度Li,就可以表征出斜边名义剪切速率。
因此,对于浆体斜面最底端外沿(图2中D′点)的名义流动速度vi可以表征为:
(8)
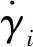
(9)
(10)
根据式(4)和式(9)分别计算浆体最底层外沿浆体的剪切应力和名义剪切速率,作图拟合后即可求得浆体的塑性粘度。
Roessel等[12]推导得出,当浆体停止流动时的剪切应力即为屈服应力,因而按照侧面滑移模型,浆体的屈服应力可以用浆体停止流动时的最大扩展半径xmax代入式(4)求得。
2 扩展度动态测量试验方法与装置
为记录浆体扩展半径的动态变化,采用由微型坍落度筒、玻璃框架、高速摄像头及电脑组成的测试装置,如图4所示。玻璃框架顶面玻璃板上贴有靶形透明刻度。

图4 摄像装置、坍落度筒尺寸示意图Fig.4 Schematic diagrams of camera device and slump cone size
试验时,开启录像装置后,5 s内缓慢提起坍落度筒。采用高速摄像机对浆体的坍落过程进行拍摄,待录像完成后,采用专用视频软件逐帧播放,通过图像分析软件读取每一时刻浆体的面积,计算浆体在任意时刻的扩展半径(xi)。
3 试验与验证
3.1 不同水灰比水泥浆体动态扩展度测试
采用冀东P·O 42.5R水泥,分别选用0.40~0.44五组不同水灰比(W/C)的水泥浆体进行扩展度动态测量试验,其扩展度在180~320 mm范围内。水泥浆组成、容重和最终扩展度如表1所示。

表1 不同水灰比水泥浆体的参数Table 1 Parameters of cement paste with different water cement ratios
通过动态测量获得不同水灰比水泥浆体扩展度(2xi)随时间变化规律,如图5所示。由图5可知,浆体扩展度随时间延长呈现非线性变化,可以分为三个阶段:第一个阶段是最初0.01 s内,扩展度变化较小;第二阶段是随后的匀速扩展过程;第三阶段是在0.05 s之后,浆体的扩展速度又降低。出现这三个阶段的原因是在坍落初期,浆体从坍落度筒中流出时,会受到筒壁的粘附阻力作用,使得底层浆体实际受到的压力减小,因而浆体初始扩展度变化较小。待坍落度筒完全提起后,底层浆体受力均匀,扩展度变化速率趋于稳定。而坍落后期,浆体底面半径逐渐增大,浆体高度显著减小,因浆体总体积有限,使得浆体的扩展速度减慢。上述三个阶段中,在第二个阶段(0.01~0.05 s时),水泥浆体扩展速度较为稳定,扩展度随时间变化曲线的斜率接近线性,该阶段与侧面滑移模型的假设较为吻合,因此对该阶段的xi-ti数据,采用侧面滑移模型计算浆体的剪切应力和名义剪切速率。
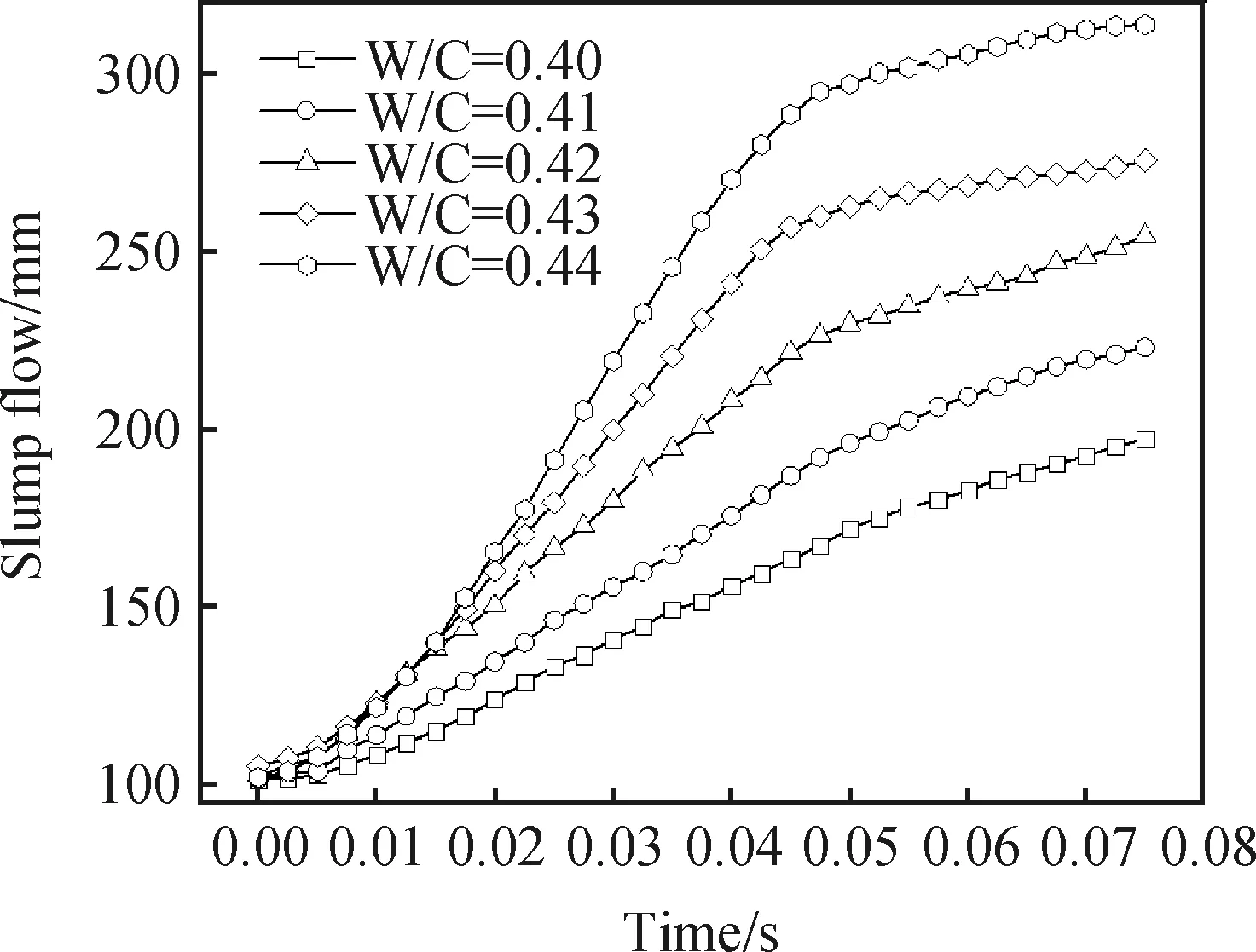
图5 不同水灰比水泥浆体动态扩展度与时间的关系Fig.5 Relationship between dynamic slump flow and time of cement paste with different water cement ratios
3.2 剪切应力与名义剪切速率的计算
3.2.1 剪切应力
根据式(4)计算剪切应力值随时间的变化,如图6所示。从图6可以看出,随着时间的延长,斜边剪切应力逐渐降低,初始剪切应力降低速度较快,后期剪切应力降低速度逐渐变慢。

图6 不同水灰比浆体剪切应力计算值与时间的关系Fig.6 Relationship between calculated values of shear stress and time of cement paste with different water cement ratios
3.2.2 名义剪切速率
根据图5的xi-ti数据,代入式(7),计算求得不同时刻的水泥浆截锥体斜边长Li,如图7所示。从图7可以看出,在浆体扩展过程中,浆体的斜边长Li会随着ti的增加呈现先减小后增加的变化趋势,表明浆体在坍落扩展过程中斜边长Li先被压缩而后被拉伸。这是由于浆体斜面最底端外沿(见图2中D′点)浆体受到玻璃底板的约束,其流动受限。如果没有底板的约束,在斜边剪切应力的作用下其流动应该是加快的,因此在计算D′点的名义流动速度时,用Li的前项减去后项,使初始阶段名义流动速度为正值。利用式(8)计算不同时刻的名义流动速度vi值,做vi-ti曲线如图8所示。
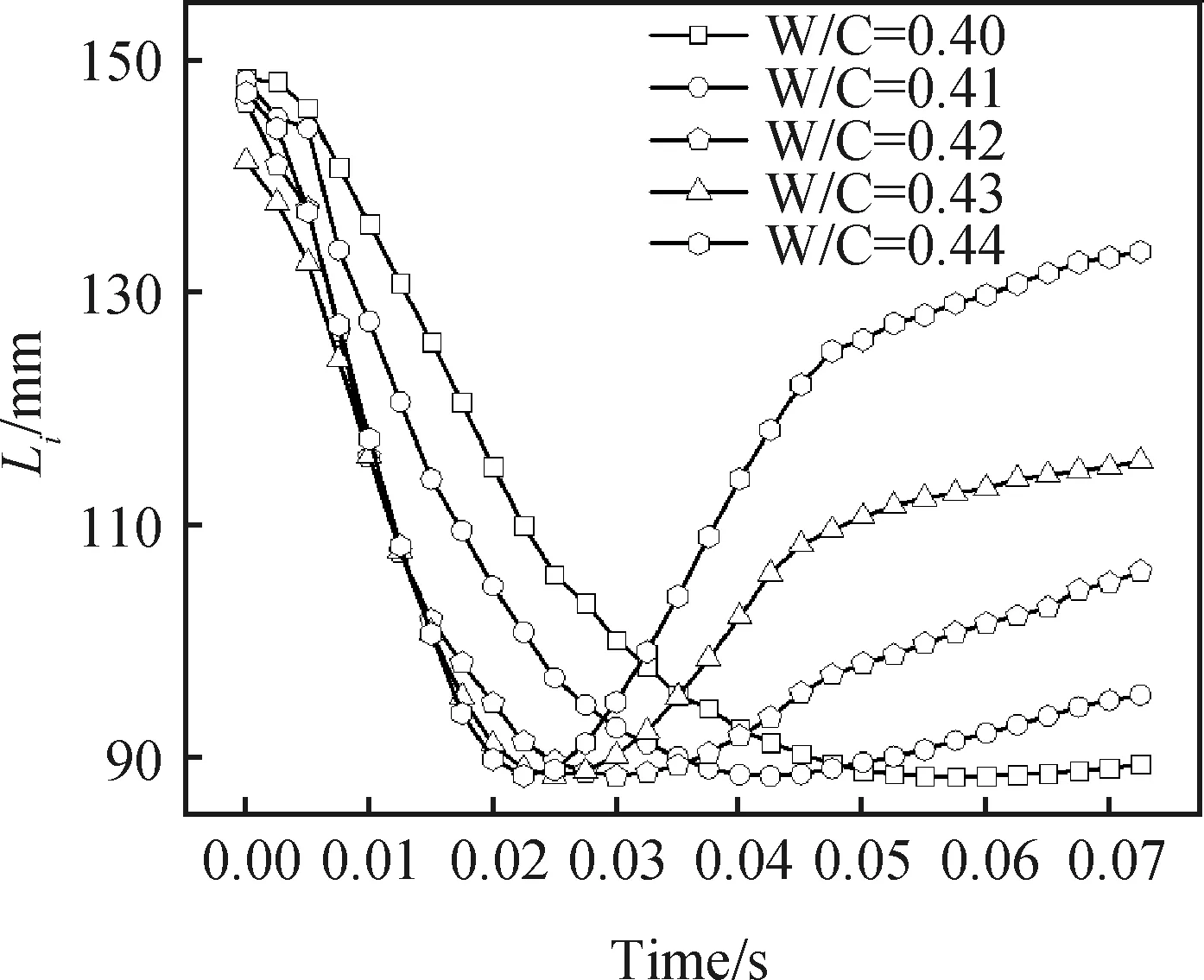
图7 截锥体斜边长计算值随时间变化曲线Fig.7 Variation curves of the calculated value of the hypotenuse of circular truncated cone over time

图8 浆体斜边名义流动速度随时间变化曲线Fig.8 Variation curves of hypotenuse nominal flow velocity of cement paste over time
从图8可以看出,初始时(0.01 s内)浆体斜面最底端外沿的名义流动速度迅速增大,随后放慢,此时斜边长度逐渐变短,接着名义流动速度变为负值,此时斜边被拉伸,而后名义流动速度又变缓,最终速度趋于0 mm·s-1,流动停止。
3.2.3 塑性粘度与屈服应力的确定
图5中0.01~0.05 s扩展度随时间延长呈线性增长,将该阶段名义流动速度vi代入式(9)计算出浆体ti时刻的名义剪切速率,结合式(4)计算的剪切应力计算值,可得扩展度线性变化阶段的名义剪切速率与剪切应力对应关系,如表2所示。由于斜边在压缩阶段时其变化量为负值,因此表2中W/C=0.41~0.44时的名义剪切速率在压缩段为负值。
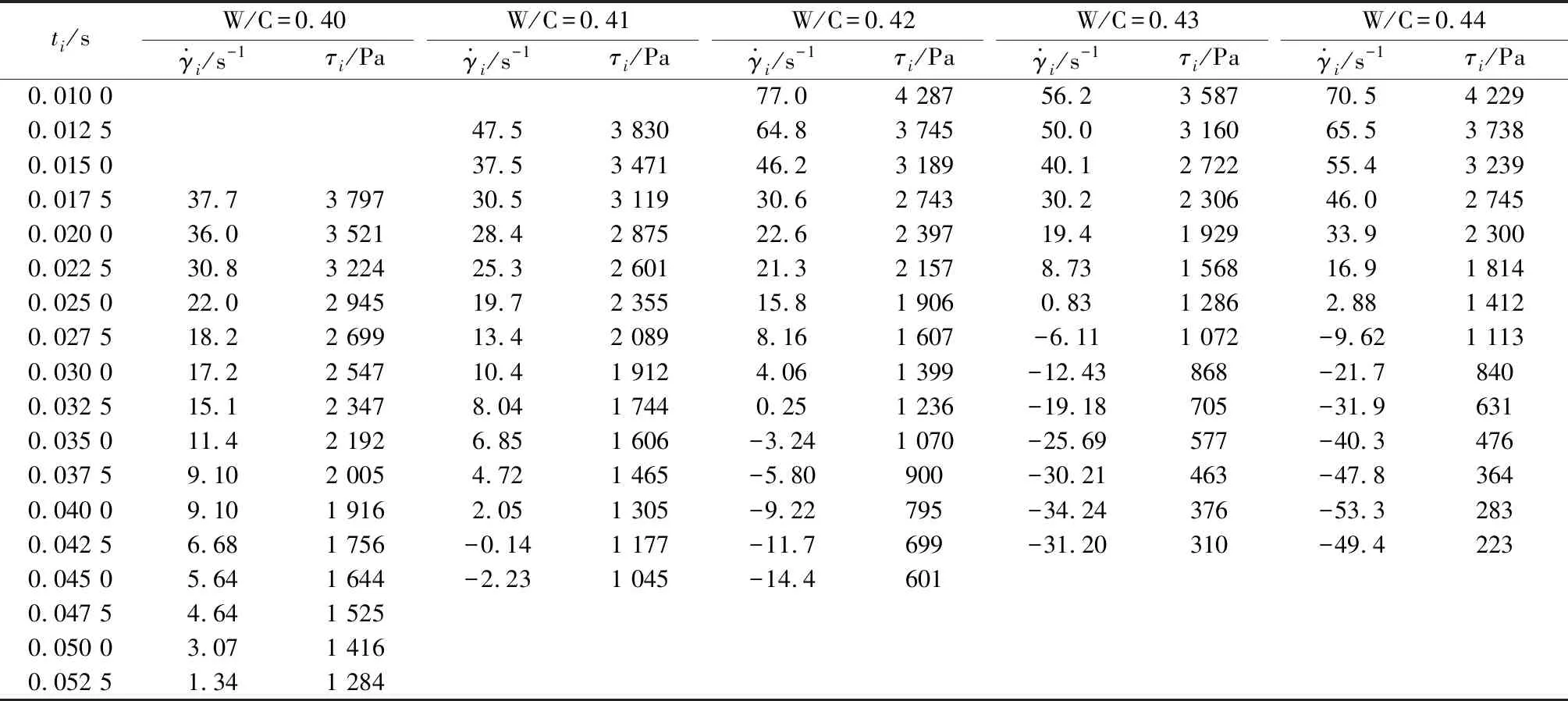
表2 剪切应力与剪切速率计算值Table 2 Calculated values of shear stress and shear rate

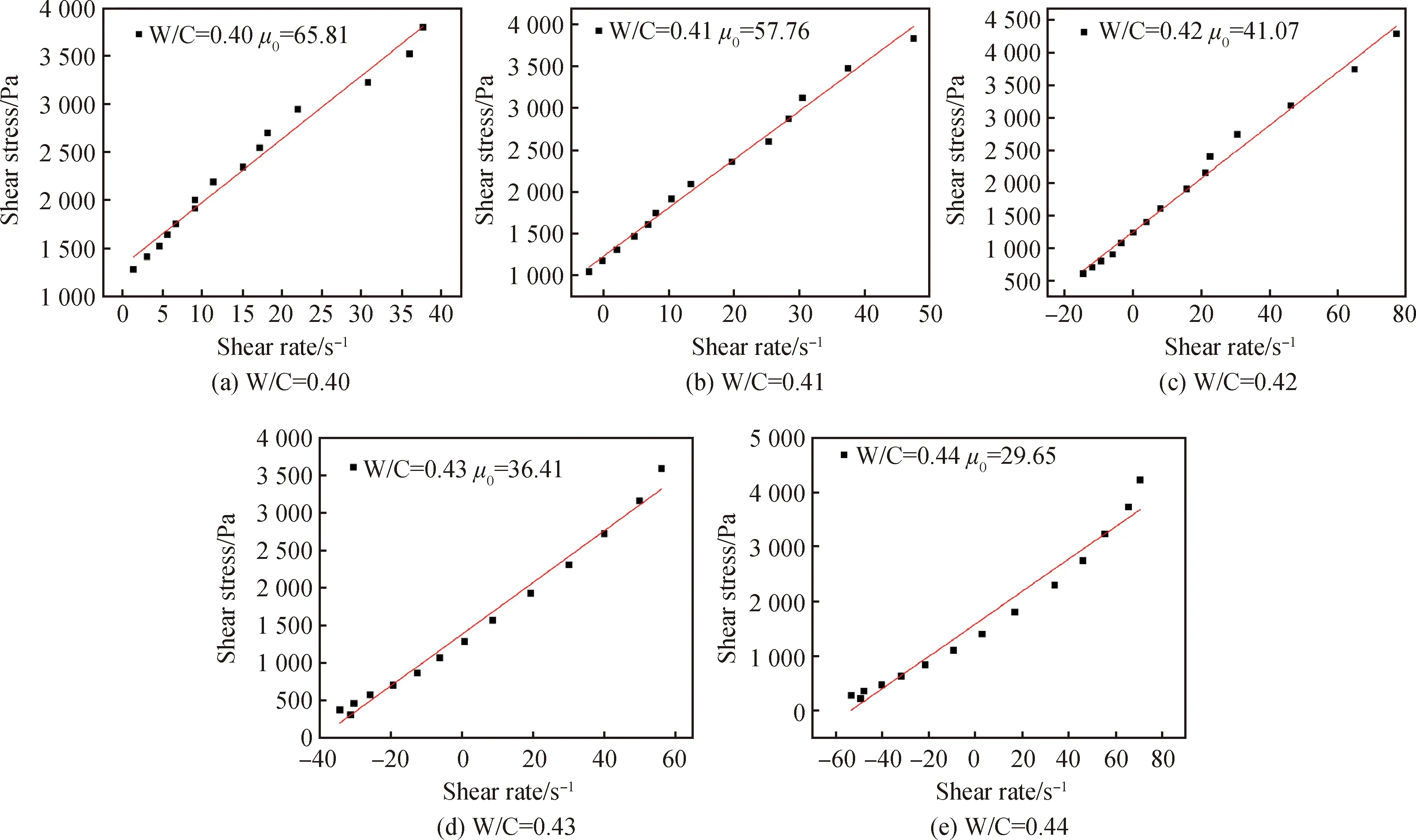
图9 不同水灰比水泥浆体匀速扩展阶段曲线 curves of cement paste with different water cement ratios in uniform change stage

表3 屈服应力与塑性粘度计算值Table 3 Calculated values of yield stress and plastic viscosity
从表3可见,随着水灰比增加,水泥浆体的塑性粘度μ0和屈服应力τ0均逐渐减小。
3.3 塑形粘度与屈服应力的验证
采用DV2-T旋转粘度计,选取转速为1~13 r/min,速度梯度为1 r/min,测试前述水泥浆体在不同剪切速率下的剪切应力和剪切速率,如图10所示。

图10 旋转粘度计拟合曲线Fig.10 Fitting curves measured by rotary viscometer
对图10的数据进行线性拟合,得到不同水灰比水泥浆体的塑性粘度和屈服应力旋转粘度计测定值μm和τm,结果如表4所示。


表4 不同水灰比水泥浆体的塑性粘度与屈服应力测定值Table 4 Measured value of yield stress and plastic viscosity of cement paste with different water cement ratios

图11 不同水灰比水泥浆体的塑性粘度与屈服应力修正值与测量值比较Fig.11 Comparison between the corrected value and the measured value of plastic viscosity and yield stress of cement paste with different water cement ratios
从图11可看出,经修正后的屈服应力和塑性粘度计算值与旋转粘度计测量值具有良好的吻合性,表明通过扩展度动态测量采用侧面滑移模型表征水泥浆体屈服应力和塑性粘度是可行的。
4 结 论
(1)扩展度动态测量表明,流动度较大的水泥浆体扩展过程可以分为慢速扩展、匀速扩展和减速扩展三个阶段。
(2)对水泥浆体匀速扩展的第二阶段,通过扩展度动态测量采用侧面滑移模型可以计算浆体的剪切应力和名义剪切速率,通过拟合可以求得浆体的塑性粘度。浆体的屈服应力可以用最大扩展半径通过公式计算求得。
(3)采用侧面滑移模型计算得到的水泥浆体塑性粘度与屈服应力计算值,经过比例系数修正后,与旋转粘度计测定值之间有良好的吻合性。

