声呐浮标漂浮性能分析

程浩

（第七一五研究所，杭州，310023）

声呐浮标（下文简称浮标）是一种主要的航空搜潜装备，空投入水后，漂浮装置保持直立姿态漂浮于水面。水下传感器借助传输电缆下沉到预设的工作深度，将接收到的目标信号经过放大、滤波等处理，调制成高频信号，天线向空中发射，由飞机上的设备进行接收。浮标的无线电天线和GPS天线均安装在漂浮气囊内。在波浪的激励下，浮标会出现摇摆现象，若漂浮气囊倾倒，将会减小无线电作用距离，导致GPS位置信息无法实时更新，影响通信链路的稳定性和可靠性。浮标是一种系列化的多类型产品，各种类型的组成模块大同小异，本文根据浮标的重心位置、浮心位置及摇摆的固有周期，研究浮标漂浮性能。

1 浮标漂浮状态

浮标处于漂浮状态时，漂浮气囊与水面电子仓形成密封舱体漂浮在水面，无线电天线和GPS卫星天线安装在漂浮气囊内，水面电子仓下悬挂有传输电缆和传感器等相关组件，如图1所示。

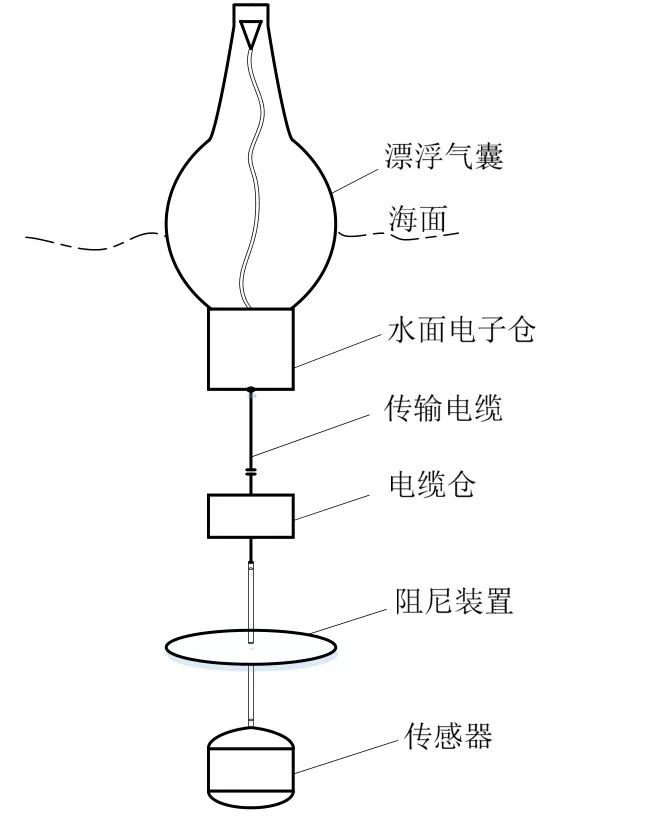
图1 浮标漂浮状态示意图

研究浮标漂浮性能时，简化水下悬挂物部分，近似为没有体积的质点附属在水面电子仓的下端面。忽略海水的阻尼力，浮标静止漂浮在海面时，受到重力、排水产生的浮力以及悬挂物的拉力。漂浮平衡条件是受到的外力之和为0。图2为浮标漂浮海面时受力情况。

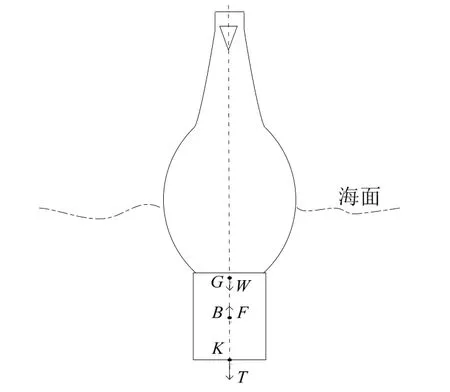
图2 浮标平衡状态受力图

浮标形状成轴对称性，浮力F的作用点即浮心B是排开水体积的形心，在中心轴线上；水面电子仓内零部件的质量几乎对称分布，故整体重心G在中心轴线上；悬挂物产生的拉力作用点设置在端面中心点K，因此，浮标静止漂浮时，重力W、浮力F和拉力T作用在同一铅垂线上，且T+W=F。

2 浮标稳定性

根据船舶稳定性理论[1]，物体悬浮在水中时，其稳定平衡的条件是重心必须在浮心之下；物体漂浮在海面时，其稳定漂浮时重心与浮心的相对位置已经不是决定因素，取决于物体转动后产生新的浮心位置。

浮标漂浮气囊的形状近似椭球形，静止状态时，水线面过对称面，水线面的形心称作漂心。如图 3所示，浮标受风浪影响摇摆时，产生倾角θ，新的倾斜水线仍过漂心，漂浮气囊出水的体积等于入水的体积，并且倾斜前后排开水的体积的大小没有变化，但随着倾斜浮标浸入水中的形状发生变化，浮心的位置由B点变为B1点；浮标的重量在倾斜前后没有改变，故重力大小及作用点与静止时相同；悬挂物通过传输电缆连接在端面上，其拉力T方向仍沿铅垂线方向，大小不变。此时，浮心和重心及拉力作用点的位置不再位于同一铅垂线上，浮力在新的浮心作用点相对于原浮心产生力矩MF，同时，拉力T相对于原浮心也产生力矩MT。重力W相对于原浮心也产生力矩Mw。将MF、Mw与MT之和定义为恢复力矩MR，若恢复力矩与倾斜力矩的方向相反，则会起到抵抗倾斜力矩的作用，MR为正值。此时，倾斜力矩消失，恢复力矩能使浮标恢复到平衡位置。若恢复力矩与倾斜力矩的方向相同，不仅不能抵抗倾斜，反而促使浮标继续倾斜，此时MR为负值。

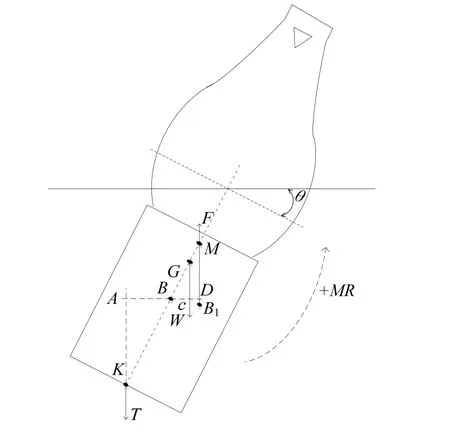
图3 浮标倾斜时受力分析

浮标倾斜时，产生的恢复力矩MR满足：

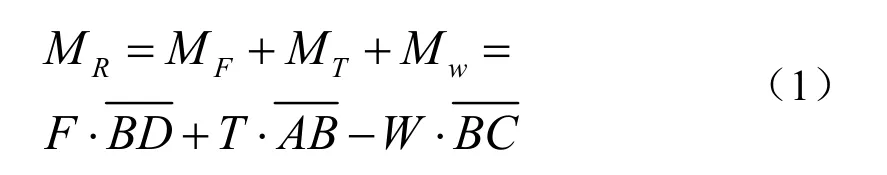
当MR等于0时，外力消失后，浮标不会回到原来位置，也不会继续倾斜。浮标倾斜前的原浮心作用点与重心作用点的连线称为浮轴，BG两点之间距离记作e；浮标倾斜后的浮力作用线与浮轴的交点称为稳心，即点M，BM两点之间距离称为稳心半径，记作r。浮标倾斜时，浮力作用线总是过稳心M[2]。

3 浮标特例分析

在某一型浮标实际使用过程中，发现无线电天线作用距离过短。对这一现象进行分析，发现浮标的漂浮气囊倒伏在水面，不能自动扶正。原因是当浮标水下悬挂物在匀速下降过程中，悬挂在水面电子仓上的悬挂物产生拉力为0，即T等于0。此种情况下，浮标倾斜时，产生的恢复力矩无法使其回正。

当浮标悬挂物拉力消失后，仅受到重力W和浮力F的共同作用。重力和浮力大小相等，方向相反，作用在同一铅垂线上。产生倾角θ时，浮力与重力形成一个力偶，使浮标回到原来平衡位置，恢复力矩MR表示为：

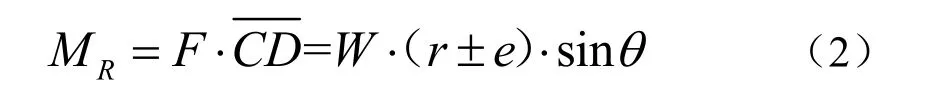
式中，e为重心与浮心间距。在进行浮标总体布局设计时，浮标的重心、浮心及稳心之间相对位置可能存在多种情况，需要对每一种情况的稳定性能进行分析。

（1）重心G在浮心B之下，浮标倾斜角为θ时，浮力与重力产生的力偶距与倾斜力矩方向相反，当外力消失时，该力偶距能使浮标恢复至平衡状态，如图4（a）所示，稳心M在重心G之上，MR为正值。

（2）重心G在浮心B之上，浮标倾斜角为θ时，浮力与重力产生的力偶距与倾斜力矩方向相反，当外力消失时，该力偶距能使浮标恢复至平衡状态，如图4（b）所示，稳心M在重心G之上，MR为正值。

（3）重心G在浮心B之上，浮标倾斜角为θ时，浮力与重力产生的力偶距与倾斜力矩方向相同，当外力消失时，浮标继续倾斜而不再恢复至原来的平衡状态，如图4（c）所示，稳心M在重心G之下，MR为负值。

（4）重心G在浮心B之上，浮标倾斜角为θ时，稳心M与重心G重合，浮力与重力产生的力偶距等于 0，当外力消失时，浮标不会回到原来位置，也不会继续倾斜，如图4（d）所示，MR为0。

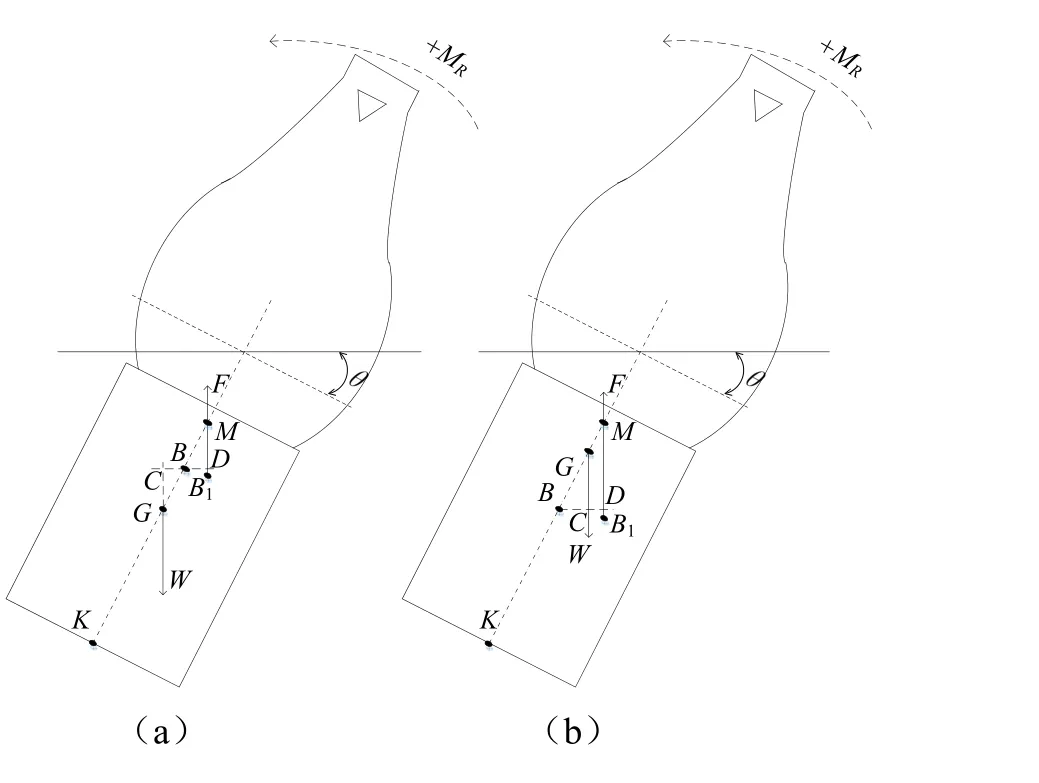
图4 浮标重心与稳心的关系

在浮标设计时，上述（3）、（4）两种情况是不允许出现的，浮标倾斜后不能恢复到原来的平衡位置。对于情况（1），重心在浮心之下，浮标倾斜时，稳心始终在重心之上，必然会产生正的恢复力矩，浮标可以自动扶正。在浮标设计时，尽量使重心在浮心之下，但是水面电子仓内要放置电池及电路板，受空间及重量的限制，有时很难做到这一点。这时可以考虑情况（2），重心在浮心之上，相距较近，使稳心在重心之上，浮标可以自动扶正，如果重心过高，就可能出现情况（3）或情况（4）。

4 浮标漂浮摇摆周期

浮标在水中自由摇摆时，可以用倾斜角和角加速度来分析运动情况。浮标摇摆时出水的体积等于入水的体积，并且是等体积倾斜，浮标自由摇摆时受到以下力矩[3-5]。

（1）恢复力矩

浮标倾斜角为θ时，产生恢复力矩MR：

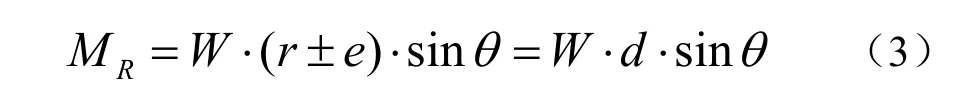
式中，d为稳心与重心间距。根据船舶原理相关知识，r可以由式（4）求得

式中，I为质量相对于过重心（质心）且垂直于纵剖面的轴的转动惯量；∇为排开水体积。

（2）阻尼力矩

物体摇摆时，与水之间存在相对速度，必然受到阻力。但是，浮标的摆动角度较小，与水接触部分体积较小，并且漂浮气囊表面光滑，所以阻尼力矩可以忽略。

（3）惯性力矩

浮标摇摆过程中存在角加速度，必然产生惯性力矩。浮标本身惯性力矩Mθ与角加速度成线性关系。

式中，μ为倾斜角的角加速度。根据平衡条件，合力矩为0，则有

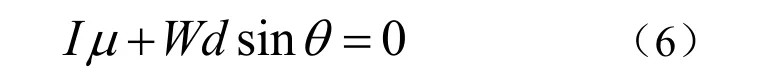
浮标倾角较小，sinθ≈θ，μ是θ的二阶导数，解方程得

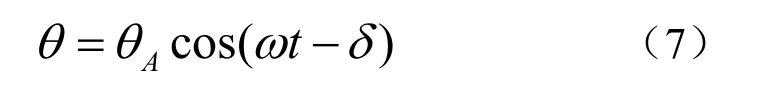
式中，Aθ为倾角幅值，t为时间，δ为初始相位角，为浮标摆动的固有频率。

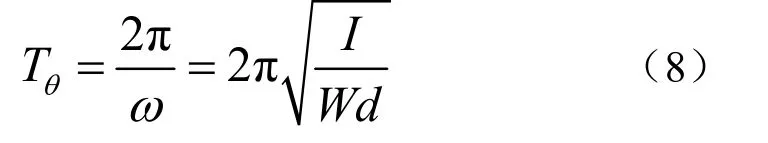
式中，Tθ浮标自由摇摆时固有周期。

浮标摇摆时，固有周期与其转动惯量、重量、重心、浮心和稳心的相对位置有关，在浮标设计时，尽量使浮标摇摆周期远离波浪起伏周期，避免产生共振。可以通过提高浮标转动惯量提高浮标固有周期，也可以通过减小稳心和重心间距与重量的乘积来提高浮标固有周期。

5 结论

浮标漂浮稳定性与重心、稳心及浮心的位置有关；摇摆周期与转动惯量、重量、稳心与重心的间距等参数有关，设计浮标时应综合考虑这些参数对稳定性和固有周期的影响。在浮标重量及浮力一定的前提下，调整浮标尺寸及内部零部件分布，增大恢复力矩，可以提高浮标抗风浪性能；从稳定性出发，重心要比稳心低，重心低一些，稳心高一些，可以增加浮标恢复力矩；但是稳心过高时，浮标摇摆固有周期短，受风浪影响摆动较剧烈。