交叉路段背景下改进的D-S证据理论地图匹配算法
滕志军,张 宇,李昊天
(1.东北电力大学 现代电力系统仿真控制与绿色电能新技术教育部重点实验室,吉林132012;2.东北电力大学 电气工程学院,吉林132012;)
随着经济的快速发展以及人口向大城市发展浪潮的兴起,城市交通越来越发达,道路越来越复杂。在实际的车辆导航中,由于GPS 的系统误差、信号的传输误差、数据的偶然误差以及电子地图的精度问题等,导致GPS 轨迹点和实际道路点存在偏差[1],这会使驾驶者偏离正确行驶路线,错误驾驶,更严重的是可能会带来交通事故。因此,一种快速、有效、准确的方法对提高导航性能尤为重要。目前主要有两种解决方法[2],一种是提高GPS 轨迹点的精度以及电子地图的精度,但该方法比较复杂,成本也比较高,特别是现在的道路日新月异,很难及时对电子地图进行更新;另一种方法是通过地图匹配对GPS 轨迹点进行一系列处理,特别是对偏离正确道路的轨迹点数据进行纠正,使其重新定位到正确道路上,该方法比较容易实现,成本也比较低,成为当前研究热点。
地图匹配技术应用广泛,为车辆导航、交通流分析、地理社交网络分析等领域[3-6]提供与位置服务相关的帮助。目前国内外提出的算法主要是针对非特定路段即普通路段,主要有基于概率的地图匹配算法[7]、基于几何的地图匹配算法[8]、基于拓扑约束的地图匹配算法[9-10]、基于权重的地图匹配算法[11-12]等。这些算法各有优缺点,原理简单、容易实现的算法匹配精度不高,原理复杂、实现难度大的算法匹配精度高。交叉路段[13]是路网中最复杂的情况,道路密度大且连接复杂,目前的地图匹配算法一般把它当作普通道路处理,极有可能造成误匹配、不匹配、匹配精度低等问题,因此交叉路段的匹配是地图匹配的难点[14]。如图1,汽车行驶在A 路段,目的地为Z 点,正准备进入连续的交叉路段,真实轨迹为A 路段到B 路段,但由于匹配错误,将轨迹点错误匹配到C 路段,此时要到达目的地则需要右拐进入D 路段,但对于真实轨迹而言,此时右拐相当于进入E 路段,离目的地越来越远,导致最终的行驶路线与正确的路线有很大不同,因此提高交叉路段的地图匹配精度对我们快速准确到达目的地有着非常重要的意义。针对交叉路段存在的问题,本文提出一种交叉路段背景下改进的D-S 证据理论算法,重点利用方向证据对传统的候选路段概率公式进行改进来弥补传统D-S 证据理论中交叉路段精确度不高的问题。

图1 错误匹配示意图Fig.1 Mismatching diagram
1 地图匹配算法的实现
1.1 数据预处理
在地图匹配前,首先要对数据进行预处理。数据预处理由两个部分组成:剔除异常数据并插值[15]补全缺失的数据和生成网格索引。
1.1.1 剔除异常数据并补全缺失的数据
城市道路路况复杂,存在隧道、高架桥和密集的高大建筑物等,可能会影响GPS 信号的传输,从而使接收机获取的数据异常。为了减小异常数据对匹配性能的影响,需要对GPS 数据进行处理,剔除异常数据并利用插值法根据两个连续的车辆历史定位点来补全下一个缺失的数据。定位点中包含的信息有:经纬度、车辆速度、车辆行驶方向与正北方向的夹角、时间戳等。剔除原理如图2所示,插值原理如图3所示。
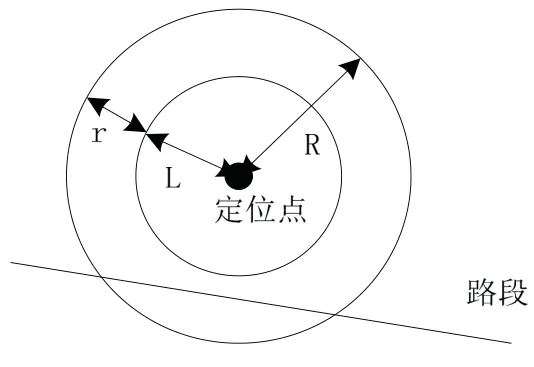
图2 剔除原理图Fig.2 Schematic of elimination
本文设置一个距离阈值R,对超过阈值范围的定位点进行剔除,距离阈值由两部分共同决定,分别是车辆最大偏移量和定位误差。
由式(1)首先计算车辆的最大速度Vmax。

其中Vtmax为道路最高限速,Vs为瞬时速度误差。故车辆最大偏移量L 为:

其中Δt为采样间隔。r 为一定置信水平下定位数据的误差圆半径,由此可得距离阈值。

定位点到路段的距离超过距离阈值,则该定位点剔除,否则保留该定位点。

图3 插值原理图Fig.3 Schematic of interpolation
由于在交叉路段车辆采样频率较高,因此任何两个相邻采样点经过的路段可以看成是直线路段。本文插值后的定位点坐标如式(4)(5)所示,其中(xi,yi)表示当前需插值补全的定位点坐标,(xi-1,yi-1)表示车辆前一个历史定位点坐标,vi-1为车辆前一历史定位点行驶速度,ψi-1、ψi-2分别表示车辆在前两个定位点时的行驶方向与正北方向的夹角。

1.1.2 生成网格索引
地图匹配过程中需要获取GPS 定位点的候选路段,最基础的方法是每获得一个定位点就查询一次电子地图中的整个道路网络,该方法比较精确但会导致耗时较长,从而影响匹配性能,因此本文引入网格索引[16],从而减少查询时间、快速地获取候选路段。网格索引的基本思想是,将整个电子地图分成若干个格网,提前算出每个网格中所包含的或相交的路段。当进行查询时,首先确定对象所在的格网,然后再快速查询所在网格所包含的候选路段,大大提高查询速度。
1.2 候选集获取
对定位数据预处理后,根据定位数据信息来确定实际道路所在的大致区域,目前常用方法是根据概率确定一个误差椭圆,该椭圆区域内包含车辆位置。误差椭圆推导公式为:

其中,a、b分别是椭圆长、短半轴,σX和σY分别是定位点经度和纬度的标准差,σXY是协方差,φ是椭圆长半轴与正北方向的夹角,σ0是可调因子。由以上椭圆公式可以看出,相关参量计算比较复杂,因此本文对其进行简化,减少计算开销,简化后的椭圆中心为当前定位点Pi(xi,yi),其相关参量计算为:

2a'、2c'分别为简化后的椭圆的长轴和焦距。在简化后的椭圆中,基于网格索引确定轨迹点所处的网格,并查询以该网格为中心的3×3 的网格内误差圆中所包含的或与误差圆相切的路段作为候选路段。设从误差圆中提取的全部候选道路集合为D={S1,S2,…Si,…,Sk|i=1,2…k},过程如图4所示,点O为轨迹点,K、L、M、N 为以该轨迹点为中心的3×3网格中的路段,在这些路段中寻找误差圆中包含的或与误差圆相切的路段,最终得到点O 的候选路段为M和N。

图4 获取候选路段示意图Fig.4 The diagram of obtaining the candidate road section
1.3 基于交叉路段的D-S 证据理论地图匹配算法
1.3.1 距离的概率分配函数m1(Si)
距离是地图匹配算法中最主要的判断准则,某一定位点最有可能的真实位置就是在距离其最近的道路上。根据距离的远近给定位点的所有候选路段分配不同的概率m1(Si),其中i=1,2,3…k。且定位点的所有候选路段距离的概率之和为1。距离证据函数αi构造为

式中di为GPS 定位点到候选路段Si的最短距离,距离的概率分配函数构造如式(12)。

如图5,计算距离di时,分为两种情形(P1和P2为定位点),设定位点坐标为(x,y),道路两端端点的坐标为M(x1,y1),N(x2,y2)。

图5 最短距离计算Fig.5 Calculation of shortest distance
①定位点P1在路段MN 上的投影点为P3,且P3在道路上,则线段P1P3的长度即为所求的最短距离d1。
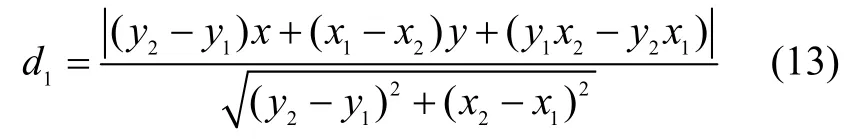
②定位点P2在路段NM 上的投影点为P4,但P4并不在路段上,而是在它的延长线上,此时取距离P2最近的道路点为M,最短距离d2即为线段P2M 的长度。
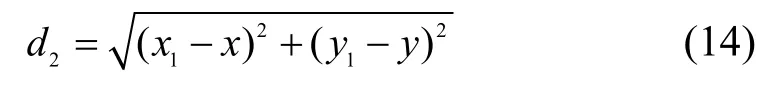
1.3.2 方向的概率分配函数m2(Si)
方向是车辆周围存在较多候选道路时确定匹配路段的另一判断准则。在考虑方向时,直接计算车辆行驶方向与所属道路方向之间夹角比较复杂,本文中先得出车辆行驶方向与正北方向的夹角以及所属道路方向与正北方向的夹角,然后将两夹角作差即可得出车辆行驶方向与所属道路方向之间的夹角。根据两者之间夹角的大小对定位点的所有候选路段分配不同的概率m2(Si),其中i=1,2,3…k。同样定位点的所有候选路段方向的概率之和为1。方向证据函数βi构造为

式中θi为车辆行进方向与所属道路方向之间的夹角,则方向的概率分配函数定义式为

如图6所示,在道路Si上选取一直线路段并在其上任选两点(记为P 和Q),以P 为原点,设Q 坐标为(x3,y3),通过式(17)计算可得道路Si与北向夹角γi。

图6 道路方向与车辆方向夹角示意图Fig.6 The diagram of the angle between the road direction and the vehicle direction

若x3=0,y3<0,则γi=π;x3=0,y3>0,则γi=0。
至于车辆与北向夹角ψ,目前许多定位软件可直接获取。
综上所述,车辆行进方向与所属道路方向之间差值θi为式(18)。
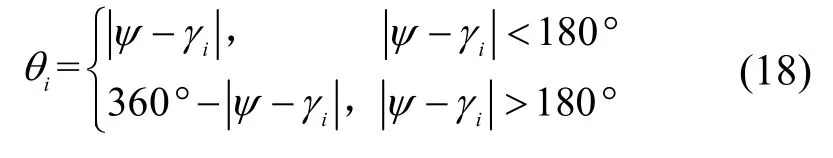
1.3.3 候选路段概率计算
本文研究对象为交叉路段,其定位点有可能在各条道路之间,由于各道路之间的方向角相差较大,因此相对距离信息而言,方向信息的可靠性较强。基于方向信息匹配到第i条路段的可信度取决于匹配到除第i条路段以外的其它路段,即匹配到除第i条路段以外的其它路段的概率越小,匹配到第i条路段的可信度就越大。因此可信度定义如式(19)。

在求出了距离的概率分配函数m1(Si)和方向的概率分配函数m2(Si)以及可信度之后,进行候选路段概率计算,候选路段概率公式构造如式(20)。

其中,F、G是GPS 点的候选路段。选取该真实GPS点概率最大值对应的候选路段作为该GPS 点的匹配路段,即认为当前时刻车辆在该路段上。
1.3.4 算法步骤和流程
步骤1:对数据进行预处理。设阈值去除异常数据,插值补全缺失数据,并进行网格索引减少匹配时间。
步骤2:根据简化的误差圆获取候选道路集。
步骤3:计算距离和方向的基本概率函数。
步骤4:根据方向证据定义可信度。
步骤5:改进候选路段概率公式,计算轨迹点的所有候选路段概率。
步骤6:对候选路段概率进行排序,概率最大值对应的路段即为匹配路段。
2 算法的实测验证与仿真比较
2.1 实测验证
为了验证改进型地图匹配算法性能,对算法进行模拟实测验证。定位模块选取车载导航常用的GPSUM220 双模模块,采样频率为2 Hz。本文在多种主要为交叉路段的城市路网环境下进行测试。

图8 实测匹配轨迹Fig.8 Measured matching trajectory
图8为本文算法下的一个匹配图,各定位点能很好地匹配到所行驶的道路上,在连续的多个交叉路段仍能有极高的匹配准确率。
2.2 仿真比较
图9为直接投影算法、传统D-S 证据理论算法、曲线拟合匹配算法和本文改进D-S 证据理论匹配算法四种不同地图匹配算法在相同条件下的各自匹配准确率仿真图。其中算法的准确率是用匹配正确的定位点数与获得的总定位点数的比值来衡量。可以看出,本文算法在平行路段的匹配准确率相对于其它地图匹配算法要低,但在交叉路段其匹配准确率极高,匹配率约为97%,对比其它方法在准确率上至少提高4%,这是由于本文算法是针对交叉路段,重点使用方向信息,因此本文算法在交叉路段最适用,但对于侧重于距离信息的平行路段则效果较差,在匹配准确率上比不上针对非特定路段的其它三种算法。

图9 匹配准确率对比Fig.9 Comparison of matching accuracy
图10~13 分别为四种算法在候选路段条数分别为2、3、4、5 时的单点匹配时间的仿真结果。其中,蓝色曲线是直接投影算法,绿色曲线是传统D-S 证据理论算法,黑色曲线是曲线拟合算法,红色曲线是本文算法。匹配时间为从获取定位点到确定候选路段所需的平均时间。由四幅图横向对比来看,随着候选区域内候选路段的增加,本文算法单点匹配时间虽也随之增加但增幅最少,当候选区域内有两条候选路段时,本文算法的单点匹配时间为4.2 ms 左右,当候选区域内有五条候选道路时,本文算法单点匹配 时间仅为5.4 ms 左右。由四幅图纵向对比来看,在四种算法中,不论候选区域内有几条候选道路,本文改进算法的单点匹配时间均低于其它算法,总体而言,本文算法在时间上至少可提高1 ms 左右。实时性较好。
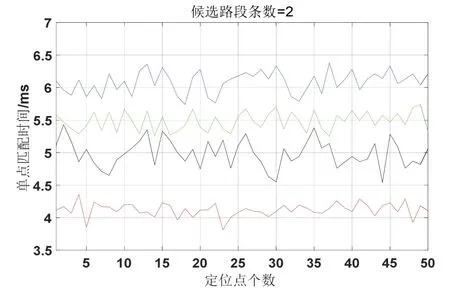
图10 两条候选路段时对应的单点匹配时间Fig.10 Single point matching time for two candidate road sections

图11 三条候选路段时对应的单点匹配时间Fig.11 Single point matching time for three candidate road sections

图12 四条候选路段时对应的单点匹配时间Fig.12 Single point matching time for four candidate road sections
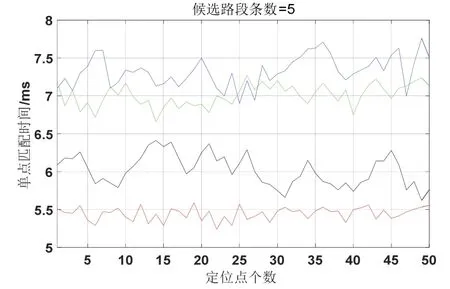
图13 五条候选路段时对应的单点匹配时间Fig.13 Single point matching time for five candidate road sections
3 结 论
本文以交叉路段为研究对象,提出一种交叉路段背景下改进的D-S 证据理论地图匹配算法,通过设置距离阈值剔除异常点,并借助插值法补全缺失点,简化误差椭圆减少匹配时间,构造方向和距离的基本概率函数及引入可信度改进候选概率函数,最终确定匹配路段。结果表明,该算法提高了匹配精度并缩短了定位点的单点匹配时间,能很好地解决交叉路段匹配难的问题。

