一种IMU全零偏快速标定方法

王岁儿，杨功流，王丽芬，刘鹏娇

（1.北京航空航天大学，北京 100191；2.航天工程大学，北京 100141；3.中国电子科技集团公司第五十四研究所 石家庄 050081）

捷联惯性导航系统（SINS）具备自主性好、隐蔽性高、抗干扰强、导航精度高及可实时连续输出高频姿态、位置、速度等特点，已广泛应用于军事和民用领域。然而，惯性测量单元（IMU）的零偏及初始姿态误差是SINS 导航误差快速发散主要误差源，即惯性导航系统的精度主要依赖于IMU 精度。因此，对IMU 全部零偏的标定和补偿是减少初始姿态误差和提高SINS 导航精度的有效方法[1-2]。

惯导系统使用前需要进行充分的室内标定工作，但是由于惯性器件自身误差特性，陀螺仪及加速度计零偏每次启动会有变化，且在一次启动后会随着时间、环境产生漂移。传统的IMU 零偏标定通常在惯导系统初始对准阶段利用卡尔曼滤波进行估计。但是对于静止惯导系统，IMU 零偏间存在耦合，仅部分零偏可观测可估计，静基座精对准仅可估计北向陀螺零偏、天向加速度计零偏。常用的二位置对准虽然可以实现部分解耦，但是仅仅可估计水平陀螺零偏，不能估计天向陀螺零偏[3]。此外，需要转位机构、转台等测试设备辅助实现多位置对准，亦或通过载体的设定机动来增加可观测度[4]。对于旋转调制型惯导系统，这些转位编排很容易实现，但是对于捷联惯导系统零偏估计非常困难，此外规定载体的机动则限制了惯导系统的适用性。

然而，这些方法需要设计转位、机动编排[5]。此外精对准要使零偏状态收敛需要较长的时间。李建利[6]分析了解析粗对准姿态误差，提出一种通过任意2个静态姿态三轴陀螺仪零偏标定方法，但是该方法并未给出加速度计零偏的标定方案。卢佳振[7]结合文献[6]陀螺零偏标定方法，提出了一种航姿系统用加速度计零偏标定方法，但是该方法需要设计三个IMU 不同姿态，从而避免奇异，这给实际工程应用零偏标定带来不便。文献[8]提出一种外场的标定方案，该方法利用重力模值观测的无迹卡尔曼滤波对加速度计进行标定，陀螺采用系统级标定方案，但是该方法至少需要12 位置转位而且还需要至少30 分钟才可对所有参数完成标定。显然，这不适用于外场快速零偏标定。

综上所述，传统的零偏估计方法存在IMU 零偏不能完全估计、滤波收敛较慢等问题；此外，多位置零偏估计方法需要转位机构、转台等测试设备，不适用于外场的零偏标定测试需求。因此，本文基于静基座解析粗对准姿态矩阵非正交、非单位化误差与北向、天向陀螺零偏及天向加速度计零偏关系[9]，提出了一种三位置快速IMU 全部常值零偏标定方法，所提出的方法快速方便简洁，仅需要6 分钟就可完成测漂，不需要其他的转台等专用测试设备，仅需要提供IMU 可放置水平面，特别适用于外场工程实际测漂试验，方便灵活。本文通过仿真试验及战术级光纤陀螺IMU 的测试验证方法的有效性。

1 解析粗对准姿态矩阵误差分析

捷联惯导系统解析粗对准的目的是获得载体系（b系，右前上）与导航系（n系，东北天）间方向余弦矩阵，通过b系及对应n系内一组三维线性不相关的矢量计算获得。假设地球上某一点P点重力加速度和地球自转角速度在导航系内表示如下:

其中gP,Ω 为P点的重力加速度幅值和地球自转角速度幅值，L为当地纬度。静态条件下，不考虑惯性器件的误差，P点重力加速度和地球自转角速度在载体系内表示如下:

则初始对准姿态矩阵由式(3)计算

将式(1)、(2)带入式(3)展开成矩阵为

姿态矩阵的欧拉角表示如式(5)所示

其中 s （⋅）、c （⋅）分别为正弦、余弦算子，俯仰角θ、滚转角γ、方位角φ通过式(6)计算

以上分析都是基于惯性器件无噪声的理想情况，但对于实际捷联惯导系统，由于惯性器件受零偏、随机游走等误差项影响，通过式(4)计算的姿态矩阵包含误差矩阵E，如式(7)所示[1-2]。

从式(7)可得到姿态误差矩阵为:

根据文献[1][2]以及文献[6][9]对解析粗对准误差的分析，解析粗对准姿态误差主要由两部分构成，对准误差和非正交、非单位化误差，如式(10)所示。

其中，Ess为对准姿态误差，Es为非正交、非单位化误差:

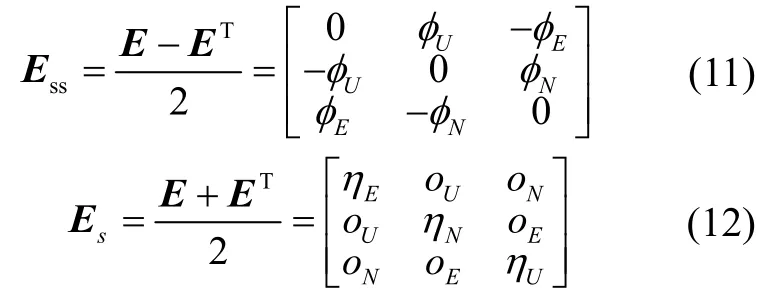
考虑到惯性器件误差，静态加速度计以及陀螺的输出测量值可写成:

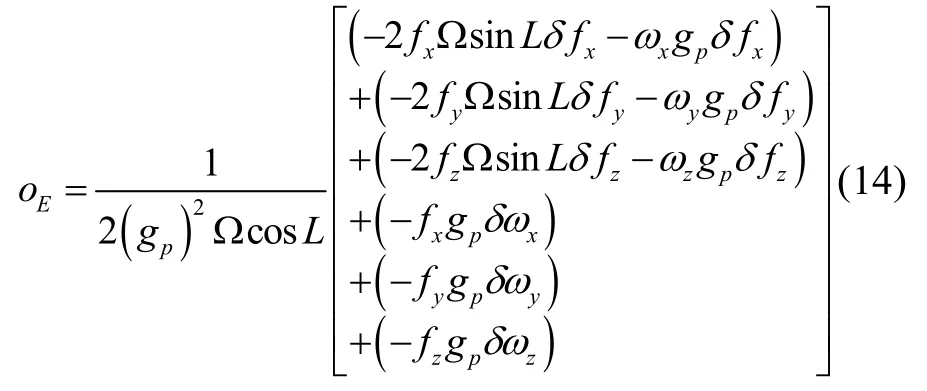
非单位化误差为:

考虑到惯导系统姿态可能为任意值，从而导致公式不统一，因此将惯性器件零偏统一到导航系，惯性器件零偏在导航系内表示为:

将式(20)代入式(4)中，式(21)为加速度计零偏在导航系的表示，式(22)为陀螺零偏在导航系的表示。

将式(21)(22)带入式(17)(18)(19)中，对应于ηE，ηN，ηU合并、整理化简可得:

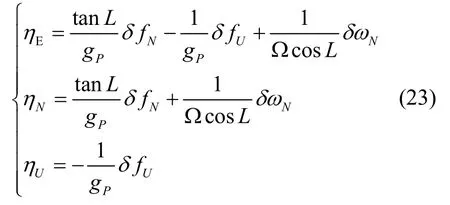
对应于式(14)oE合并同类项，整理化简可得:

结合式(23)(24)，可获得天向加速度零偏、北向和天向陀螺零偏的表达式如下:

2 三位置IMU 全零偏快速标定方法

参考文献[1][2][9]，对准姿态矩阵的非正交、非单位化误差可以通过解析粗姿态矩阵获得。

虽然式(27)中包含北向陀螺零偏的计算公式，但是在实际应用中让IMU 某一轴向朝北向很不容易，也失去了快速零偏标定的意义，而让IMU 轴向指向天很好实现。因此设计了三位置IMU 零偏快速标定方法，只需要IMU 的三个轴向依次指向天，仅计算天向加速度计零偏、天向陀螺零偏。IMU 的三次位置编排如图1所示。该方法非常适用于外场的IMU 零偏快速标定，且只需要为IMU 提供一个朝上放置的平台即可。

图1 三位置零偏标定编排Fig.1 Arrangement of three-position biases estimation scheme

三位置对应的IMU 零偏标定公式为:

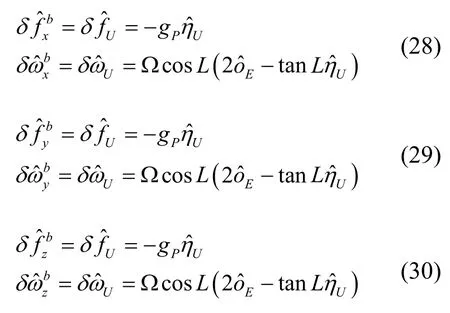
按照图1的标定编排以及式（28）-（30），这样IMU零偏可全部标定。为了快速实现IMU 零偏标定，图1中每个位置仅采集2 分钟IMU 静止数据，则整个IMU零偏标定需6 分钟即可完成。此外，采集的数据也可迭代计算，多次迭代能更精确的标定IMU 零偏。所提出的快速零偏标定方案，简洁方便可行。

在理想测试条件下，b系与n系天向轴重合。但对外场复杂环境，考虑测试平面倾斜或惯导系统外壳体不平倾斜记为b′系，由倾斜角引起的两坐标系天向轴不重合，等效到IMU 天向加速度计、陀螺零偏误差为式（31）:

3 快速IMU 全零偏标定试验

3.1 仿真试验

为了验证本文提出的方法有效性，设计相应的仿真试验，选用战术级光纤陀螺惯导系统作为仿真对象。设惯导系统在北航新主楼（所处纬度为北纬39.9772 °）。为了便于识别每个轴向IMU 的零偏，设置的仿真用IMU 的精度如表1所示。

表1 仿真光纤陀螺惯导系统性能指标Tab.1 Performance of simulated FOG INS

按照图1三位置编排，每个位置生成2 分钟仿真数据，仿真频率为100 Hz。通过式(28)-(30)计算零偏，并进行两次迭代计算，标定的IMU零偏如表2所示。从表2中可以看出，本文零偏标定方法可标定90%以上的陀螺零偏，可标定95%以上的加速度计零偏，且第二次迭代后，标定零偏精度有一定的提高。

为了充分验证算法的有效性、可行性，进行了100次蒙特卡洛零偏标定仿真试验，实验结果如图2、图3所示，精度统计如表3所示。通过仿真试验结果，三位置快速零偏标定方法可对IMU 所有零偏进行有效的标定，验证了算法的有效性及可行性。

表2 仿真试验结果Tab.2 Simulation results

图2 三位置100 次蒙特卡洛加速度计零偏标定结果Fig.2 Biases estimation results of accelerometers for 100 Monte Carlo by three-position scheme

图3 三位置100 次蒙特卡洛陀螺仪零偏标定结果Fig.3 Biases estimation results of gyros for 100 Monte Carlo by three-position scheme

表3 100 次蒙特卡洛仿真结果统计Tab.3 Statistics of 100 Monte Carlo simulation results

3.2 静态试验

为了更进一步验证快速IMU 全零偏标定算法，选用一套战术级光纤陀螺惯导系统进行零偏标定试验，图4所示为光纤陀螺惯导系统及对应的数据采集装置。所选系统陀螺零偏稳定性:＜0.5 ° /h，加速度计零偏稳定性:＜ 0.2 mg。

在大理石平台上开展了零偏标定试验，在试验开始前，启动系统预热半个小时，进行三位置零偏标定试验，每组数据采集两分钟，采集完成某一轴向后手动翻转惯导系统，使得另一轴指朝上，待所有数据采集完成后，按照零偏标定算法，计算惯性器件零偏。考虑到一次启动后零偏在短时间内基本稳定，系统不断电连续进行6次三位置试验。计算的零偏结果如表4所示。

图4 战术级光纤陀螺IMU 及数据采集设备Fig.4 Tactical fiber optic gyroscope IMU and data acquisition equipment

表4 三位置6 次零偏标定结果Tab.4 Biases estimation results of three-position scheme for 6 times tests

为了更进一步验证零偏标定的有效性，开展了对准试验。如图5所示，左边为高精度光纤陀螺惯导系统，陀螺零偏稳定性:＜0.01 ° /h，加速度计零偏稳定性:＜100μg。以高精度惯导系统的对准结果（俯仰角:0.043 °，横滚角:-0.072 °，航向角:269.014 °）作为参考值。进行了三次对准试验，试验对比分析了零偏补偿前后对准结果。

初始对准的姿态误差主要和水平加速度计零偏以及等效东向陀螺零偏相关。如表5所示，在补偿标定的零偏后，对准精度提高了约一个数量级，再次说明了本文提出的IMU 零偏标定算法的正确有效性。

图5 对准验证实验图Fig.5 Alignment verification experiment

表5 对准试验结果Tab.5 The results of alignment test

3.3 纯惯导解算实验

在零偏标定试验结束后，系统不断电继续采集IMU静态约1 h 数据，对准后进行纯惯导解算。作为对比，将补偿零偏和未补偿零偏的导航结果绘制在同一图上，如图6～8 所示。试验结果表明补偿零偏后，系统导航精度明显的提高，也再次验证了本文提出算法的有效性。

图6 纯惯性解算姿态结果Fig.6 Attitude result of pure inertia solution

图7 纯惯性解算速度误差Fig.7 Velocity error of pure inertia solution

图8 纯惯性解算位置Fig.8 Position of pure inertia solution

4 结 论

本文提出了一种IMU 全零偏快速标定方法，该方法仅采集IMU 每个轴向分别朝天（地）静态2 分钟数据，就可以对所有轴向的陀螺、加速度计的零偏进行标定。该方法仅需要提供IMU 静止放置的水平面，特别适用于外场测试。仿真试验表明，本文提出的快速全零偏标定方法可以标定95%以上的加速度计零偏、90%以上的陀螺零偏。战术级光纤陀螺系统的零偏标定试验、对准以及1 小时纯惯性导航试验结果，进一步验证了所述的全零偏标定方法有效、可行。虽然以战术级光纤陀螺惯导系统为试验对象，但是该全零偏标定方法也可应于更高精度的惯导系统。