考虑幅相频畸变的激光惯导圆锥补偿算法设计
翁 浚,陈学忠,刘健宁
(西安理工大学机械与精密仪器工程学院,西安710048)
关 键 字:圆锥补偿算法;幅相频特性;减振器;相对算法误差
圆锥补偿算法是捷联惯导系统算法设计重要组成部分,其对惯性导航精度的保证具有重要意义,因此国内外专家都进行了深入研究。文献[1]在圆锥补偿算法设计时,首次引入了标准圆锥运动优化系数的概念,推导了三子样补偿算法的标准公式,该公式在实际算法设计中得到了广泛的应用。文献[2]指出标准圆锥环境下,等间隔的角增量叉积是相等的,且只与更新间隔的长度有关,基于这一特性,圆锥算法的补偿形式得到了简化。文献[3]创新性地提出了一种新的基于频率特性的圆锥算法设计方案,该算法能够根据载体导航所处的运动环境的频域特性,设计适用于某个频段的优化补偿算法,提高了算法在高频段的补偿精度。
国内多位捷联惯导领域的学者也对圆锥补偿算法进行了深入研究。文献[4]利用陀螺输出的角增量信息的前两个计算周期和当前时刻陀螺采样值,通过重叠式采样的方法进行圆锥误差补偿,该算法减少了由等效旋转矢量算法引入的圆锥误差,提高了姿态解算精度。文献[5]考虑了高阶圆锥误差补偿,提出的旋转矢量微分方程高阶皮卡德分量算法在高动态振动环境下提高了导航精度。文献[6]根据圆锥误差积分和多项式系数向量叉积运算的特性,得出任意多样本的最佳圆锥补偿系数,更利于编程实现。文献[7]提出了一种改进的二阶圆锥补偿算法来抑制振动对惯导系统的影响。
现有的圆锥补偿算法基本上都是针对陀螺输出为理想的情况,而在实际激光捷联惯导系统中,激光陀螺的幅相频特性及减振器的带宽会对圆锥补偿算法精度产生不可忽视的影响,有必要针对实际器件的物理特性设计适用于指定系统的补偿算法。
1 减振器带宽与激光陀螺的幅相频畸变
由于设计、配重等原因,惯导系统的质心和形心一般无法完全重合,外部环境的振动将会引入内台体的小幅角晃动。下面通过一个简化的解析模型来描述惯导系统对振动干扰源的响应[8-10]。

图1 简化的惯性组件振动响应示意图Fig.1 Simplified vibration response diagram of inertial components
如图1所示,xF为惯性测量单元(Inertial Measurement Unit,IMU)壳体振动输入位移,x,x1,2分别为传感器组件中心点和两个连接点处的位移;θ为传感器组件由振动输入引起的角度响应;ki,ci(i=1,2)为IMU 壳体与传感器组件间安装接口处的弹簧和阻尼系数;L,l分别为惯性传感器组件的直径和半径;δl为传感器组件质心相对几何中心的距离。
经推导,加速度输入引入的角度响应的拉氏变换[11]

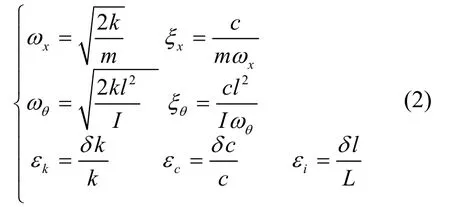
式中,ωx,ξx为线振动无阻尼自然频率和阻尼比;ωθ,ξθ为角晃动无阻尼自然频率和阻尼比,εk,εc,εl为归一化的弹性、阻尼和距离误差参数。
将式(2)代入式(1)后整理得

设置一组典型的减振器参数如下

对应的幅相频响应曲线如图1所示。

如图2所示,减振器能够衰减100 Hz 以上的振动干扰。从频域上看,圆锥补偿算法在设计时应该只考虑减振器通带范围内的影响。
激光陀螺通过抖动轮安装在台体上,其传递函数可以表示为

式中,ωn为抖轮的谐振圆频率,激光陀螺的抖动频率一般在300 ~ 600 Hz 之间。
假设某激光陀螺的抖动频率为fdither=475 Hz,抖动幅值为6',陀螺的品质因子q为50。则该抖动机构的幅相频响应曲线如图3所示。

图3 水平方向的抖动机构的幅相频响应曲线Fig.3 Amplitude-phase-frequency response curve of the horizontal dithering mechanism
可以看出,在减振器的通带范围内,激光陀螺的幅相频畸变都很小,但不为0,这也意味着采用传统圆锥补偿算法的效果未必是最优的。
2 改进的圆锥补偿算法设计
标准圆锥运动环境下,考虑陀螺的幅相频特性,陀螺敏感载体角增量变化值如下
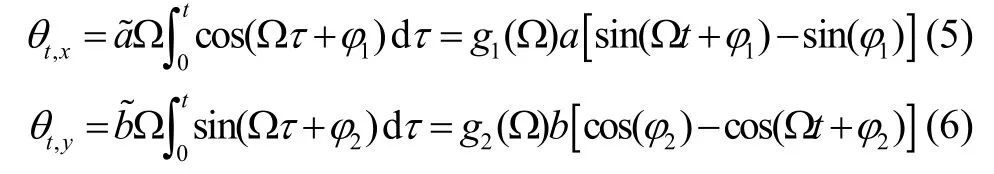
式中,θt,x和θt,y分别表示陀螺在水平两个轴向在t时刻的角度;Ω 为角晃动圆频率;a和b分别为两个轴向的晃动幅值,上标“~”表示陀螺测量得到的幅值信息,g1(Ω)和g2(Ω)表示考虑了抖动机构和数字滤波影响的角度幅值;φ1和φ2分别表示由于抖动机构和数字滤波引入的相位延迟。
一个姿态更新周期的旋转矢量增量

式中,Δθ为一个姿态更新周期内的角增量积分;Δφc为圆锥补偿项。在如式(5)和式(6)描述的标准圆锥运动环境下,Δθ仅对水平分量产生影响,而圆锥补偿项Δφc会在天向分量产生常值项。
依据圆锥项的补偿公式

式中,M为一个姿态更新周期内的圆锥补偿次数;角增量及其积分第m个圆锥补偿周期的初始时刻tl-1,m=tm-1+ (m-1)Δtl,圆锥补偿周期的结束时刻tl,m=tm-1+mΔtl;Δφc1为过去角增量的积分αm与当前补偿周期的角增量Δθm对姿态更新的影响:Δφc2对每个圆锥补偿周期内需要补偿的部分求和。其中δφc(m)的计算采用所有子样之间的叉乘积之和来进行补偿。
Δφc1和δφc(m)项的计算涉及到两个不同积分周期的叉乘项,如:i,j两个不同积分区间的陀螺增量Δθi和Δθj的叉乘项

式中,

Δt为陀螺数据的积分时间间隔;ti-1,tj-1为i,j积分区间的初始时刻。将式(10)代入式(9),整理得
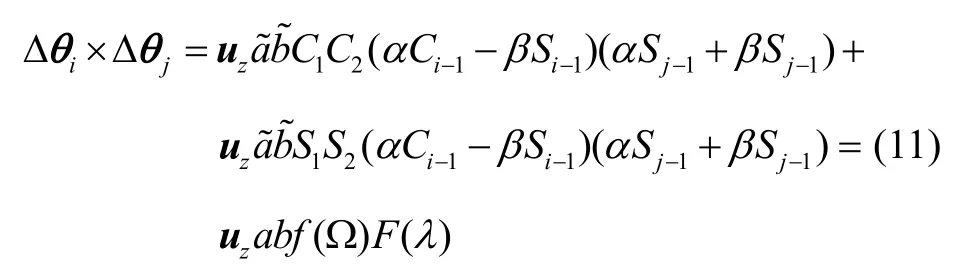
其中,

由式(11)和式(12)可以看出,陀螺不同时间周期内角增量的叉乘项结果是仅与采样间隔(j-i)、圆锥运动频率Ω 和时间周期Δt相关的正弦函数。
下面分别对补偿算法式(8)中的 Δφc1,Δφc2项的值和载体应当补偿的圆锥项大小进行分析。
(1)Δφc1项
将式(12)代入式(8)的Δφc1项的计算公式,并令积分区间 Δt=Δtl,得

式中,Siλ=sin(iλ),(i=1,2…M);tm-1为姿态更新的初始时刻;tm为姿态更新的结束时刻。
令式(13)中tm-1=0,得

式(14)表示从0 时刻姿态更新到tm时刻,每个姿态更新周期内的Δφc1的值。可以看出等号右边括号内的第二项为周期项。
(2)Δφc2项
根据文献[12]中计算Δφc2项

从式(15)看出,圆锥补偿算法影响的部分是式(15)中的正弦组合项F(iλ)的加权和。
(3)需要补偿的圆锥项
环境振动引起台体晃动,两轴晃动会在对应轴向产生同频率的晃动,而在正交轴上存在一定的和频分量和差频分量。忽略正弦项的影响,可得圆锥补偿项的速率形式

Δφc1项和Δφc2项是考虑了陀螺幅相频特性后得到的圆锥补偿项的值,而载体本身需要补偿的圆锥项应当是“理想”陀螺在一个更新周期Δtm的等效旋转矢量增量。根据式(16),令积分初始时刻t0=0,可得到等效旋转矢量增量

将式(14)和式(15)相加,令积分初始时刻tm-1=0,得

式中,tm-1为算法积分的初始时刻。
将式(18)减去式(17),忽略周期项的影响,并除以圆锥补偿周期个数M,便能够得到一个圆锥更新周期内的算法误差

式中,

也被称为圆锥漂移率。式(19)两边同时除以更新周期Δtl,并令,得误差的常值分量

式中,表示补偿算法本身引入的误差漂移。式(21)的意义在于一旦算法确定后,就可以对特定环境(可以不同于算法设计时的Φ˙)下的算法精度进行评估。
式(20)中,Es(Ω)等号右边第二项乘以,得

式中,就是考虑陀螺幅相频特性条件下,圆锥补偿周期需要补偿的漂移角速率。令f(Ω)=1,得

用式(21)对算法进行评估时,需要知道评估环境,可除以式(22)得

式中,κc一般称为相对圆锥误差,表示了算法能够补偿圆锥误差的百分比,其值不再与相关。
从频域角度对圆锥补偿算法进行设计,依据加权最小二乘的FIR 数字滤波器[13,14]设计思路,将ec在感兴趣的频域范围[0,λmax]内求平方并积分,整理得

式中,E相当于在频域范围内的误差能量大小;为每个圆锥频率点处的比重,通过对不同频段内权重的设定,能使得算法在相应频段取得不同的补偿效果。
对式(25)中的待定系数求ki偏导,并令其导数为零,整理得

式中,

和
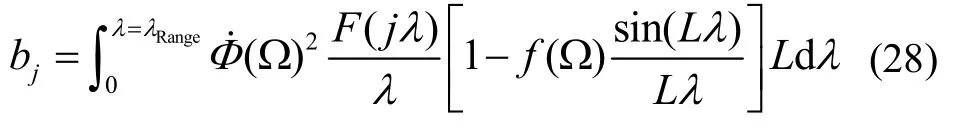
其中,j的取值范围与i相同。将式(27)和(28)写成离散形式

和

式中,dλ为离散频率考察点的分辨率,相当于每个频率点的权重系数。将式(27)写成矩阵形式为

这里给出7 种圆锥补偿算法的补偿系数,如表1所示。

表1 圆锥补偿算法系数Tab.1 Coning compensation algorithm coefficients
表1中,算法alg-0 表示不进行圆锥补偿;算法alg-1~ alg-3 为传统圆锥补偿算法系数;算法alg-1i~alg-3i 为考虑幅相频特性的圆锥补偿算法系数。惯导系统的相关仿真参数:减振器带宽100 Hz,水平两个轴向的抖动频率设为425 Hz 和475 Hz,方位轴的抖动频率为525Hz;陀螺品质因子q为50。圆锥补偿算法的设计思路是:0~100Hz内的权重,其余部分的。这样设计是希望在运动频带内的圆锥补偿精度是一致的,同时抑制非运动频带内可能产生的伪圆锥运动的影响。
3 仿真与分析
下面对传统圆锥补偿算法和本文提出的考虑幅相频特性的圆锥补偿算法在频段范围内进行对比仿真。仿真环境参数设置如下:运动轨迹为标准圆锥运动,陀螺采样频率为2 KHz,水平两个轴向的角晃动幅值a=b=0.1o,进行考察的晃动角频率范围Ω=0 ~ 200 π (rad/s),再结合式(3)的传递参数,得到图4的漂移误差曲线。
图4为抖动频率在20 Hz 处的算法漂移误差曲线,左上角图中“虚线”表示alg-0,上面三幅图中的“实线”表示算法alg-1~alg-3,下面三幅图表示算法alg-1i~alg-3i。从前面的分析和仿真可以看出,算法误差漂移曲线可能存在漂移项的同时还存在正弦项,z 轴的常值漂移率可以通过对正弦调制下的姿态误差δφz(t)进行线性拟合得到。
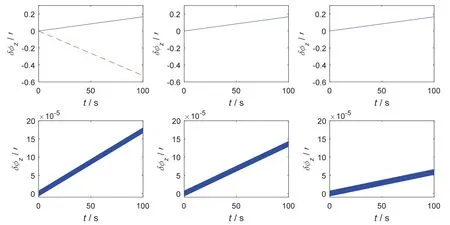
图4 抖动频率20 Hz 的算法漂移误差曲线Fig.4 Algorithm drift error curve of dithering frequency at 20 Hz
图5为标准圆锥运动下,算法相对误差的理论值和仿真结果。图中,各种类型的“点”表示如图4的圆锥误差漂移率的拟合值,“虚线”为式(25)给出的算法alg-1i 的误差公式。可以看出,误差公式(25)与采用alg-1i 补偿算法得到的多次仿真结果完全重合。
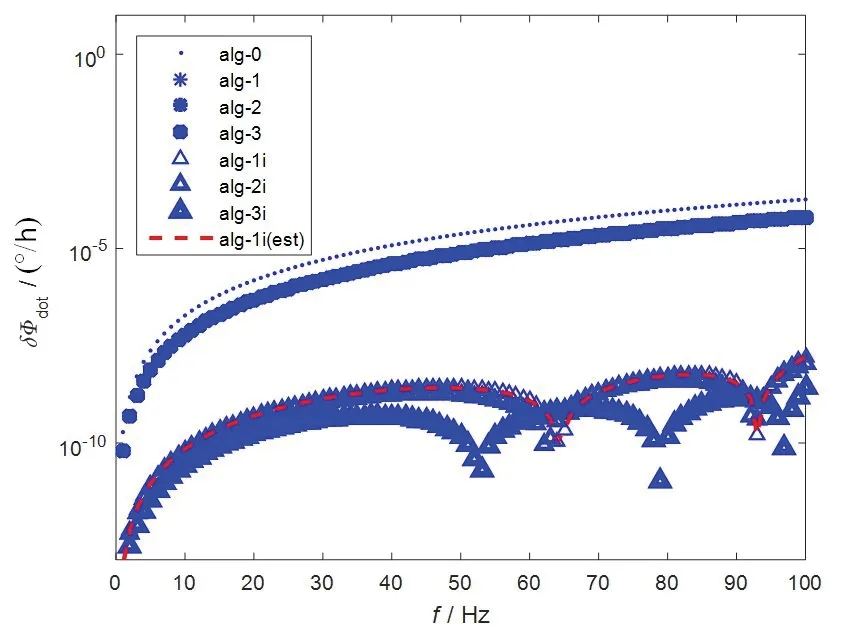
图5 仿真得到的绝对圆锥算法相对误差值Fig.5 Relative error value of absolute coning algorithm obtained by simulation
由图5可知,由于机抖陀螺的幅相频特性影响,使得传统圆锥补偿算法的精度并不高,从图5可以看出,alg-1~alg-3 三种传统算法的补偿精度基本上是相同的,即陀螺的幅相频特性使得算法没有发挥出本身的优势,相对算法误差约为31%。采用alg-1i~alg-3i的补偿算法后,算法精度随着每个补偿周期内的采样点个数增高而提高,相对算法误差在每个频率点都优于0.04%。采用alg-1i 估计的曲线与仿真得到的曲线相符合。对于捷联惯导系统来说,要求导航更新算法引入的误差影响要小于器件误差的5%。对于惯性级(陀螺零偏 1×10-2o/h)的惯导系统来说,传统算法的补偿精度在一般情况下能够满足精度要求,但对于千分级甚至更高精度的机抖激光陀螺惯导系统而言,应当在捷联算法设计时,充分考虑惯性元件幅相频特性的影响。
4 结 论
本文提出了一种考虑激光陀螺幅相频畸变和惯导系统减振器带宽,适用于激光惯导系统圆锥补偿算法的设计方法,通过合理的建模仿真,证明了改进的圆锥补偿算法设计对圆锥补偿精度有较大的提升。在算法设计过程中,改进的圆锥补偿算法使得系统在减振器带宽范围内达到最小二乘意义上最小,相对算法误差由传统方法的31%减小到0.04%。同时仿真试验也证明了圆锥补偿算法误差公式的正确性,为高精度激光陀螺惯导系统圆锥补偿算法的优化设计提供了理论支撑。

