一种针对临近空间滑跃目标的轨迹跟踪方法
秦武韬,陆小科,邢晓勇
(南京电子技术研究所,南京 210039)
随着科学技术的飞速发展,各主要国家的反导系统日臻完善[1,2],传统弹道导弹的突防能力持续下降,在此背景下,以临近空间内高速滑翔为标志的临近空间飞行器逐渐成为远程战略打击武器研发的重要方向[3,4]。美国于1987年率先开始了高超声速滑翔式飞行器(Hypersonic Glide Vehicle,HGV)项目的研究,近十年更是多次进行了HTV-2、X-51A 等临近空间飞行器的飞行试验,俄罗斯则提出了“冷”和“鹰”的研究计划,德国、日本、印度也开展了相关研究[5]。因此,研究针对临空目标的轨迹跟踪方法具有极大的理论和实际意义。与常规的轨道目标不同,临近空间飞行器不仅拥有10 马赫以上的飞行速度,还可在大气层内利用气动力进行大范围的机动飞行,其典型的跳跃式轨迹更是给雷达的高精度稳定跟踪带来了严峻挑战[6]。
在机动目标跟踪中,准确的目标运动模型是精确稳定跟踪的基础[7,8]。例如针对匀速运动的常速度模型(Constant Velocity,CV)和针对匀加速度运动的常加速度模型(Constant Acceleration,CA);对于转弯目标的跟踪问题,文献[9]则给出了协同转弯模型(Constant Turn,CT)。但CV、CA 和CT 模型均属于理想化的建模,为了应对跟踪过程中目标随时可能出现的转弯、加减速等突发机动情况,Singer 把机动控制项作为相关噪声进行建模,提出了Singer 模型,该模型在处理机动目标时具有良好的跟踪效果。文献[10]则专门针对临近空间飞行器周期性跳跃的特点提出了正弦波模型(Sine Wave,SW),较好地描述了临空目标跳跃运动的周期特性,其结果表明该方法具有比Singer 模型、Jerk模型更高的跟踪精度,文献[11]则对SW 模型做了进一步的分析和研究,并基于X-51A 轨迹验证了SW 模型的跟踪精度。
然而,以HTV-2 为代表的无动力临近空间飞行器在进行跳跃滑翔时,其能量不断减少,跳跃幅度逐渐降低,各周期的相关性持续减弱,又呈现出衰减性的特点。SW 模型在进行建模时仅考虑到了临近空间飞行器跳跃滑翔的周期性,而忽视了其衰减性,导致其在跟踪无动力临空飞行器时跟踪精度较低。因此,本文基于一种二阶时间自相关的零均值随机过程,借鉴“当前”统计模型的思想,提出了一种自适应衰减震荡模型(Adaptive Damped Oscillation,ADO)。该模型通过衰减参数和震荡参数的合理调配,实现了周期性和衰减性的有机统一,较好地描述了临空滑跃目标的运动特点。考虑到临空目标机动范围大的特点,论文在地理坐标系下推导建立了目标运动模型,利用无迹卡尔曼滤波算法设计了跟踪滤波器,并通过数学仿真对所提算法进行了验证。
1 临近空间跳跃滑翔飞行器运动描述及特性分析
1.1 目标运动描述
由于临近空间飞行器具有机动范围广的显著特点,为直观地对其运动进行描述,本文拟在地理坐标系下对其进行描述,即以经度、纬度和高度表示目标位置,以速度大小、飞行路径角和航向角表示目标速度。其中,飞行路径角γ表示速度矢量与当地水平面的夹角,航向角ψ表示速度矢量在当地水平面上的投影与正北方向的夹角。
由飞行路径角及航向角的定义,有
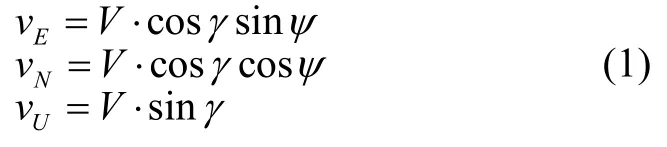
式中,V为合速度大小,vE、vN和vU分别为东向、北向和天向速度。
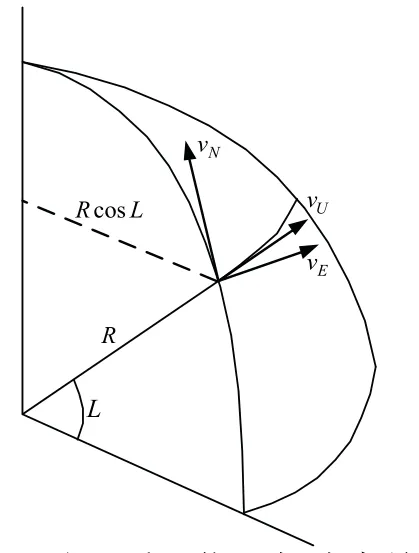
图1 地理系下位置与速度关系Fig.1 The relation of position and velocity in GEO
图1给出了经度、纬度、高度变化与东、北、天速度的关系,有:
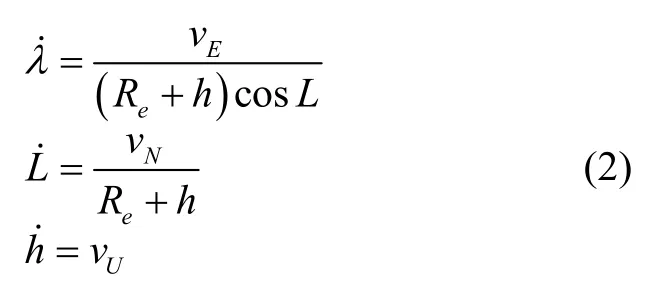
式中,λ、L和h分别表示经度、纬度和高度,Re表示地球半径。
将式(1)带入式(2),可得

1.2 运动特性分析
与传统弹道导弹不同,临近空间高速滑翔飞行器可以依靠气动力在大气层内进行高速滑翔,根据滑翔时高度方向的运动特点大致可以划分为平衡滑翔和跳跃滑翔两种模式,其中平衡滑翔模式下目标高度方向机动较小,跟踪难度较低,而跳跃滑翔模式的跟踪难度更大,因此,本文将主要对这一类型的临空目标跟踪问题进行研究。

图2 跳跃式滑翔目标运动轨迹Fig.2 The trajectory of NSHV
呈“周期性衰减”式的跳跃滑翔是临近空间飞行器所特有的飞行样式,弹道导弹、飞机等传统飞行器均无法做出类似机动。在这种机动模式下,临近空间飞行器不断上下跳跃,呈现出显著的周期性(如图2所示),此时,目标的加速度和飞行路径角也呈现出同样的周期性,各个周期间的目标运动状态强相关。但与此同时,目标又在气动阻力的作用下不断消耗能量,其速度不断下降,跳跃幅度逐渐降低,各个周期间的相关性持续减弱,表现出衰减特性。因此,临近空间跳跃滑翔目标的运动呈现出周期性与衰减性相统一的特点。
2 基于自适应衰减震荡模型的纵向机动建模
2.1 零均值衰减震荡模型
由于临空滑跃目标飞行路径角和加速度的变化规律相似,因此本文以加速度为例推导描述其衰减震荡过程的运动方程。根据临空滑跃目标周期性运动的特点,其t时刻的加速度a(t)与一个周期ΔTc后的加速度a(t+ΔTc)呈强相关。同时,随着间隔周期数的增多,目标加速度逐渐降低,该相关性逐渐减弱,表现出了相关衰减性的特点。为描述这一运动特征,可利用如下二阶时间自相关随机过程进行加速度建模,即
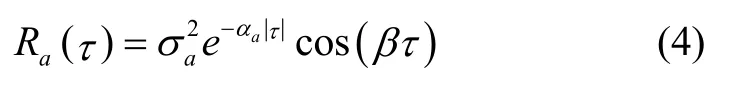
当α和β取极限值时,有:
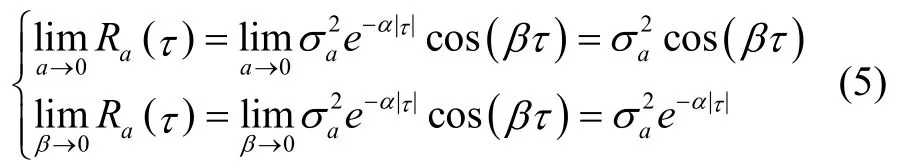
可以看出,在α逼近0 时,式(4)给出的衰减震荡模型不再具备衰减性的特点,而仅表现出周期性,其退化为SW 模型[10];当β逼近0 时,衰减震荡模型则丧失了周期性的特点,而仅表现出衰减性,其退化为Singer 模型。因此,通过参数α及β的调配,衰减震荡模型可以实现周期性和衰减性的统一。
由式(4)所给出的相关函数Ra(τ),可得其谱密度为:

其中,ω表示角速率。
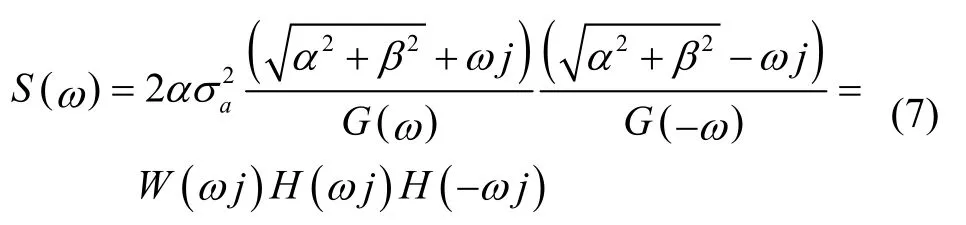
其中,W(ωj)表示白噪声的傅里叶变换。
将G(ω)代入H(ωj)中,可得

令s=ωj,式(8)可化简为
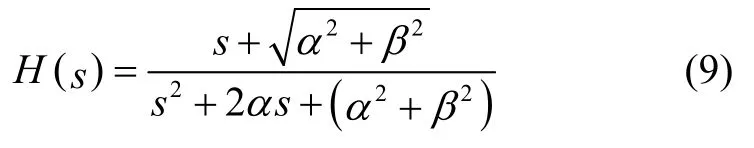
由式(9)可得衰减震荡模型下的加速度和加加速度状态方程如下:
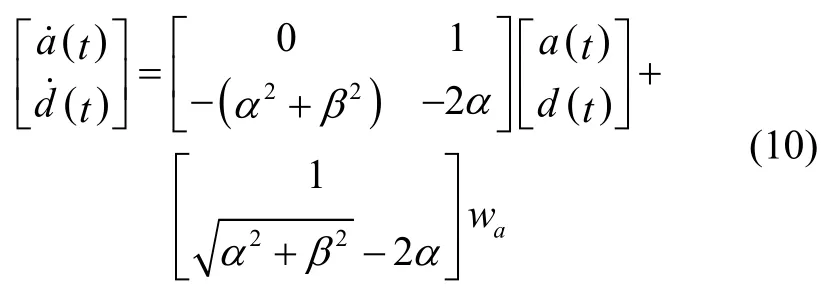
其中,wa是均值为零,方差为的高斯白噪声,d(t)为加加速度。
2.2 自适应衰减震荡模型
对于式(10)所建立的加速度变化模型,可看作SW模型和Singer 模型的组合,其中SW 模型认为目标加速度以零为均值进行周期性的跳动,Singer 模型同样认为目标机动加速度的均值为零。但事实上,临空滑跃目标在飞行过程中受气动力的作用不断减速,其加速度均值并不为零,而是随其气动外形、飞行速度和跳跃阶段的变化而变化。为更准确地对目标的加速度变化规律进行描述,本节将对式(10)所示模型做进一步改进,推导出自适应均值衰减震荡模型。
定义变量b(t)如下:

则有
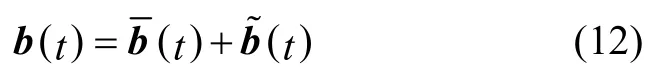
由式(10)和(12)可得
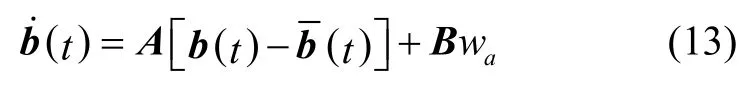
其中,
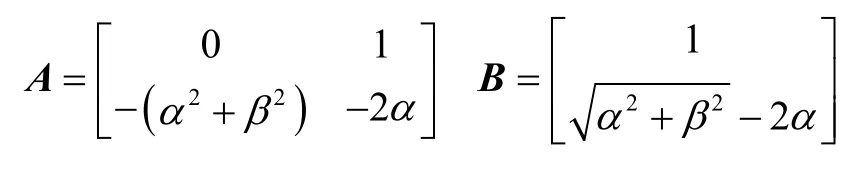
将式(13)展开,有

同理,可得飞行路径角的变化模型如下:
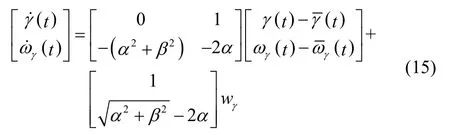
其中,ωγ(t)为飞行路径角速度,(t)和(t)为上一周期中滤波器对γ及ωγ估计值的平均,wγ是均值为零、方差为的高斯白噪声。
3 侧向运动建模及状态方程的构建
3.1 侧向运动模型
当目标进行侧向机动时,其航向角速度会随之发生变化,但由于目标飞行速度较快,受结构及气动性能的限制,下一时刻的航向角速度的变化往往有限,仅能在当前角速度的领域内,这与“当前”统计模型中关于机动加速度的假设相一致。因此,本文借鉴“当前”统计模型的思想,建立起关于航向角速度的自适应均值一阶马尔科夫模型如下:
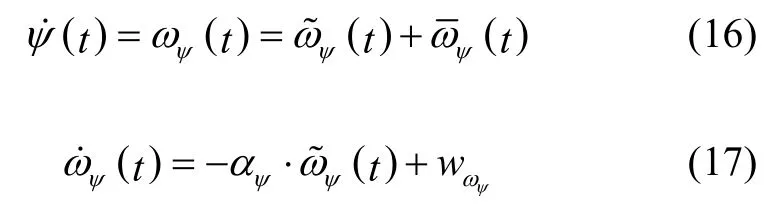
其中,(t)服从零均值一阶马尔科夫过程,(t)为航向角速度的“当前”均值,αψ为机动时间常数,wωψ为零均值高斯噪声。
根据式(16),有

结合式(16),(17)和(18),可得航向角及航向角速度的状态方程如下:
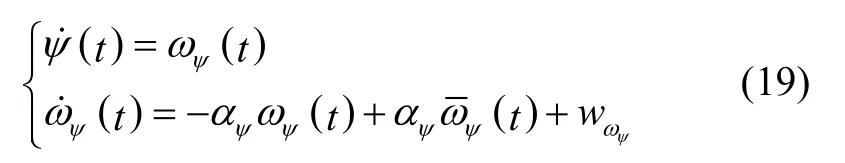
其中,航向角速度的方差为
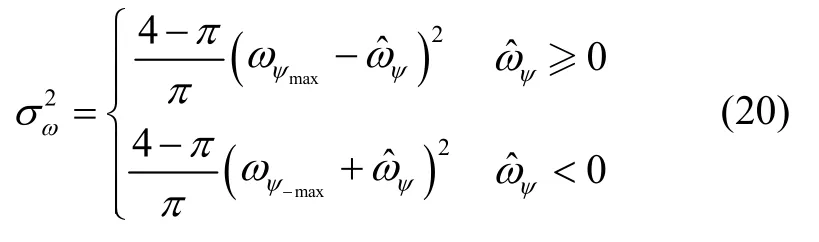
其中,为ωψ的估计值,ωψmax为最大正航向角速度,ωψ-max为最大负航向角速度。由式(20)可以看出,方差的大小与ωψmax和ωψ-max密切相关,而又直接影响到过程噪声方差阵Q 的大小。因此,为了获得更好的跟踪精度,在应用过程中需要根据目标侧向机动能力的大致情况选取合适的ωψmax和ωψ-max。
3.2 状态方程
综合上述分析,本文选取目标状态量x如下:
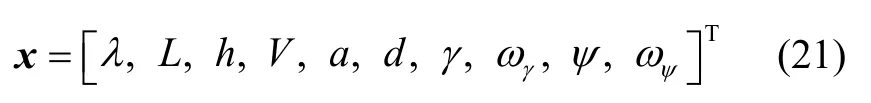
根据各状态量的定义,结合式(3)(14)(15)和(19),可建立状态方程如下:


式中,0m×n表示m行n列的零矩阵。
4 跟踪滤波器设计
现阶段,可在大范围内对非合作目标进行连续探测的设备主要包括天基红外预警卫星和雷达,但对于临空滑跃目标,其飞行过程中的红外特征不明显,无法利用红外卫星对其进行稳定跟踪。而雷达可以通过主动发射电磁波进行探测,且具有作用距离远的显著优势,可以满足对临空滑跃目标的跟踪要求。因此,本文以雷达为探测传感器建立测量模型。图3给出了雷达对目标进行探测的示意图。
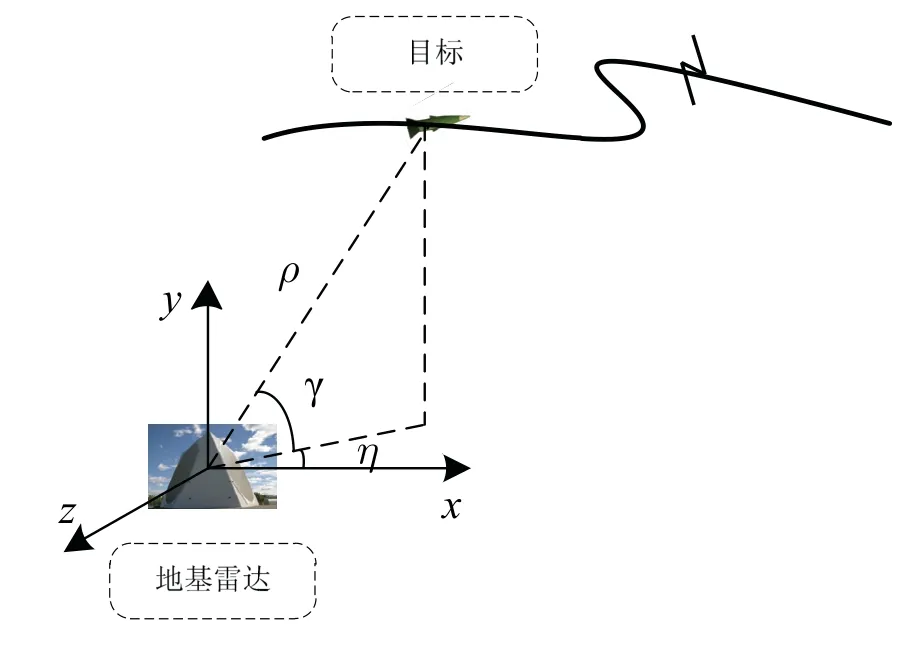
图3 雷达探测示意图Fig.3 The schematic diagram of the detection of radar
雷达通过获得目标的斜距和回波到达角对目标进行定位,因此测量量可定义为:

式中,γ为高低角,η为方位角,ρ为斜距。
则测量方程为

式中,vγ,vη和vρ表示雷达的测量误差;xe,ye和ze表示目标在雷达直角坐标系中的位置分量,有
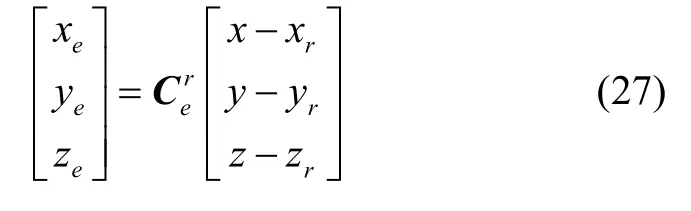
其中,地心系至雷达直角坐标系的转换矩阵,有
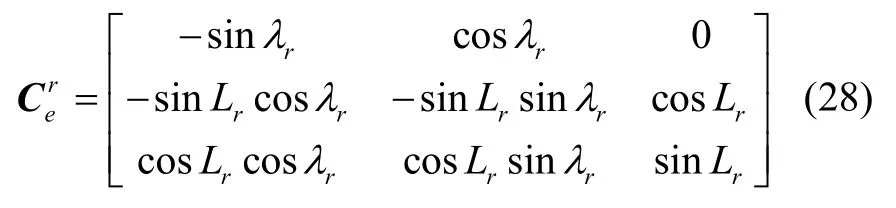
由目标在地理系下的位置信息,可得其在地心系下的位置[x,y,z]T为

同理,雷达在地心系下的位置[xr,yr,zr]T为
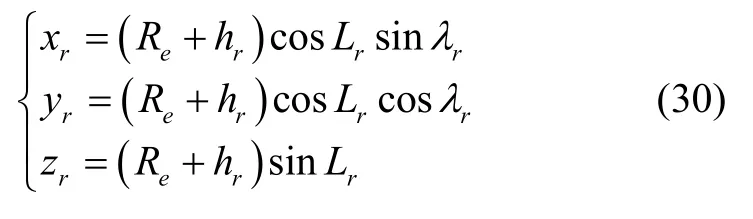
在式(30)中,[λr,Lr,hr]为雷达的经纬高位置信息,可通过标定获得。
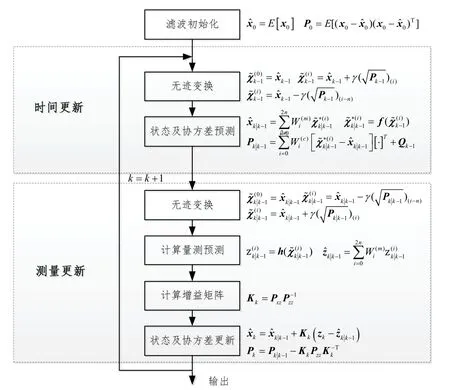
图4 无迹卡尔曼滤波算法流程图Fig.4 The flow chart of UKF
考虑到该系统的状态方程和测量方程均具有较强的非线性,且雅克比矩阵求取困难,因此论文选用无迹卡尔曼滤波算法进行滤波器的设计,图4给出了无迹卡尔曼滤波的流程图,其详细内容可参考文献[12]。
5 数学仿真分析
本文以美国X-51A 及HTV-2 的试验轨迹为参考,设置跳跃滑翔跟踪场景如图5所示,其中,目标的初始位置为[100°E,30°N,48000 m],初始速度为4800 m/s,最大飞行高度为51108 m,最小飞行高度为46449 m,跳跃周期约为150 s,飞行时间为800 s,图6给出了目标的高度变化曲线,图7给出了目标的速度和飞行路径角变化曲线。

图5 跳跃滑翔目标运动轨迹Fig.5 The trajectory of the NSHV
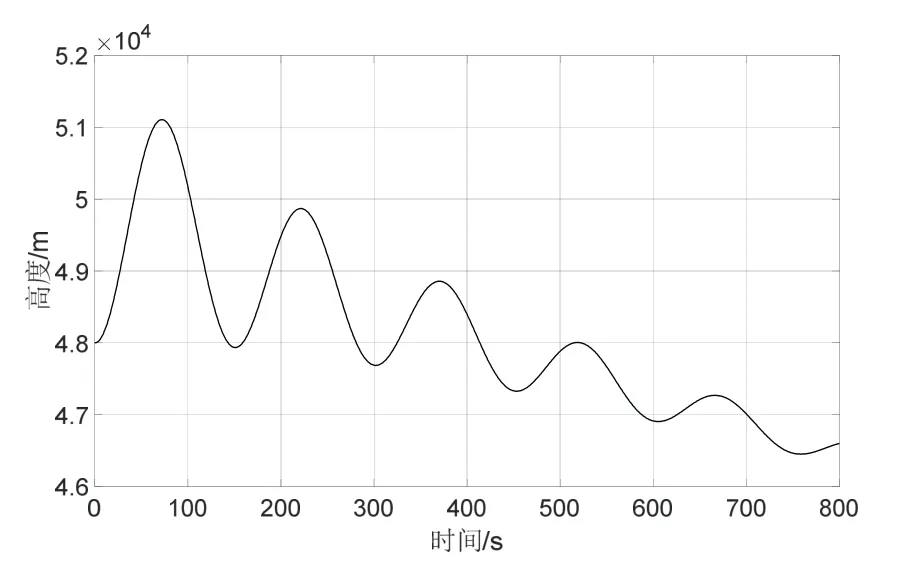
图6 高度变化曲线Fig.6 Altitude-time curve
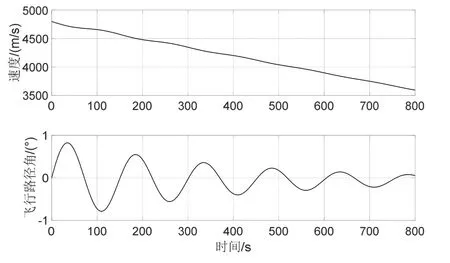
图7 速度和飞行路径角变化曲线Fig.7 The velocity-time and flight path angle-time curves
在仿真中,雷达位于[133 ° E,30 ° N,200 m],其距离测量误差σr=50m,高低角和方位角测量误差为σγ=ση=0.1°,测量频率为10 Hz。
各模型中的主要参数如下表所示:

表1 各模型中的主要参数Tab.1 Main parameters of three models
基于上述仿真场景,获得单次仿真结果如下:
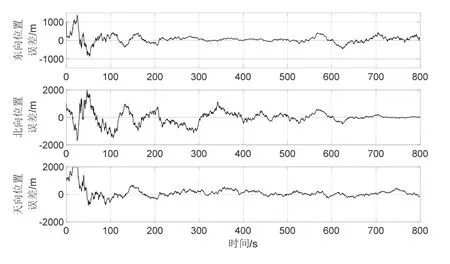
图8 东北天位置估计误差Fig.8 Position estimated error of east-north-up direction
在上述仿真结果中,图8给出了目标在东北天方向的位置估计误差,图9则给出了速度、航向角和飞行路径角估计误差,可以看出目标的位置跟踪误差在1000 m 以内,速度跟踪误差在10 m/s 以内,具有估计精度高,收敛速度快的特点。
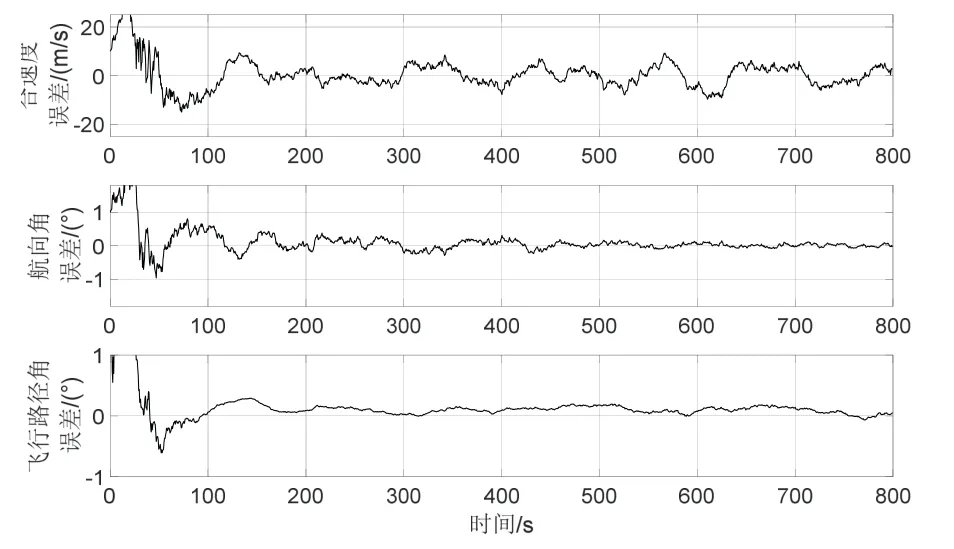
图9 速度、航向角和飞行路径角估计误差Fig.9 The estimation error of velocity,course angle and flight path angle
为进一步对比分析该算法的精度,论文分别利用常速度模型、Singer 模型、SW 模型和本文提出的自适应衰减震荡模型对临空目标进行跟踪,基于100 次独立的蒙特卡洛试验,获得仿真结果如图10所示:
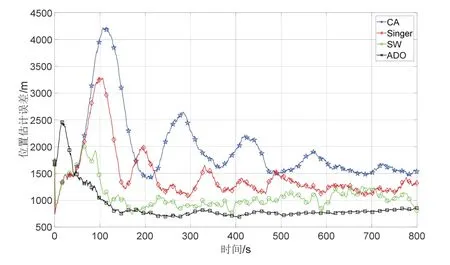
图10 位置跟踪误差对比曲线Fig.10 The comparison of position estimation error between four algorithms
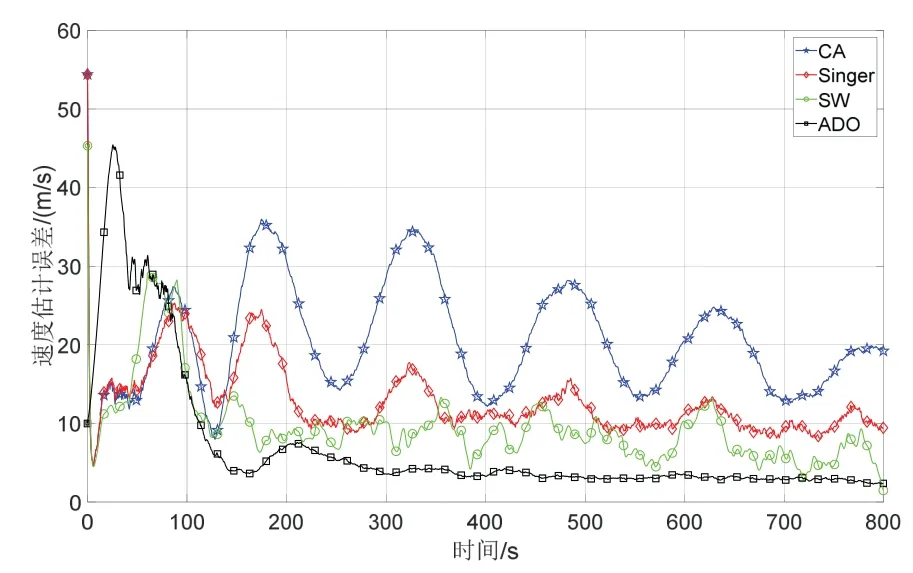
图11 速度跟踪误差对比曲线Fig.11 The comparison of velocity estimation error between four algorithms
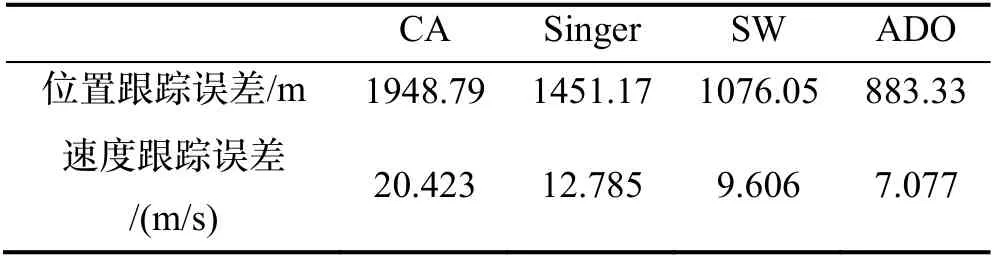
表2 各算法跟踪误差对比Tab.2 Comparison of tracking error of four algorithms
图10和图11分别给出了四种算法的位置和速度跟踪误差对比曲线,表2对跟踪误差进行了汇总。可以看出本文所提出的ADO 算法具有最高的跟踪精度,SW 模型次之,而CA 模型的跟踪精度最差。这是因为CA 模型简单地认为目标进行匀加速直线运动,这与目标的实际运动规律并不符合,导致其跟踪精度较低。同理,Singer 模型也难以对跳跃滑翔目标的运动进行描述。SW 模型认为目标进行周期性的跳跃运动,这一点较为准确地描述了跳跃滑翔目标的运动特性,但其在推导过程中假设各个周期目标的跳跃高度相等,这与临空目标的实际飞行过程不符,使得其跟踪精度略为下降。而本文所提出的自适应衰减震荡模型,不仅对临空滑翔目标的周期运动特性进行了准确描述,同时也考虑到了目标飞行过程中的衰减特性,其对目标运动的描述最为准确,因而获得了最高的轨迹跟踪精度。ADO 算法其位置跟踪精度和速度跟踪精度较SW 模型分别提高了17.91%和26.33%。
6 结 论
针对临近空间跳跃滑翔飞行器运动特性复杂,现有目标运动模型描述失准,跟踪精度较低的问题,本文基于二阶时间自相关随机过程提出了一种自适应衰减震荡模型,建立了地理系下的目标运动模型,准确描述了临近空间滑翔跳跃目标运动的周期性和衰减性。在此基础上,论文给出了雷达的测量模型并利用无迹卡尔曼滤波算法完成了跟踪滤波器的设计,数学仿真证明基于ADO 模型设计的跟踪滤波器具有比CA模型、Singer 模型和SW 模型更高的跟踪精度。

