Multi-sensor optimal placement algorithm for multi-target tracking

HUANG Fanjing ,LI Xingxiu ,WU Panlong ,HAN Xiaodong

(1.School of Automation,Nanjing University of Science ＆ Technology,Nanjing 210094,China;2.School of Science,Nanjing University of Science ＆ Technology,Nanjing 210094,China;3.Institute of Telecommunication Satellite,CAST,Beijing 100094,China)

Abstract:To solve the problem of multi-sensor placement for multi-target tracking,a multi-sensor optimal placement algorithm based on the homogeneous design and region partition is proposed.Considering each unmanned aircraft vehicle(UAV)is equipped with many sensors to provide measurement data,each UAV is regarded as a mobile sensor note.The proposed multi-sensor optimal placement algorithm is mainly divided into three steps,including the primary optimization,the quadratic optimization and the real-time path planning of sensors.Under the architecture of the proposed algorithm,the optimal sensor deployment is determined and the optimal observable target group for each sensor are assigned in real time.Furthermore,each mobile sensor is guided to track the moving targets in an optimal way.Several simulation results are given to verify the feasibility of the proposed algorithm,which shows that the quadratic optimization can obtain more suitable sensor location compared with the primary optimization.So that targets are not easy to be lost when moving.Meanwhile,the proposed algorithm can realize the reuse of sensors and save sensor resources.

Key words:target tracking;homogeneous design; multi-sensor placement; unmanned aircraft vehicle

Multi-sensor system has become an emerging research subject on account of a mass of military and civilian applications in the last few years,such as marine surveillance system,intelligent traffic system,medical rescue,criminal investigation,and so on[1-4].Since a single sensor can only acquire local state information of the environment,multiple sensors are able to provide more information,which further improves perception performance of the system[5-6].Furthermore,with the rapid development of sensor technologies,multi-sensor system can deal with larger amounts of data in the more intricate environment,which appeals a great deal of researchers to lucubrate the automatic management technology of multiple sensors[7].

Multi-sensor management is a broad concept that generally constituted of sensor deployment,sensor behavior assignment,and sensor coordination.Sensor deployment mainly concerns determining the time,location,and number of required sensors[8-9],which is the core theme of this paper.Sensor behavior assignment basically involved assigning many tasks to sensors and making action planning for sensors[10-11].Sensor coordination generally has centralized and decentralized architectures,the former of which determines all actions of sensors by a central mechanism,whereas the latter makes every sensor have the characteristic of intelligence and be automated to a certain degree[12].

The most challenge problem in multi-sensor deployment is determining the appropriate position and planning path for sensors.Typical tool is the Fisher information matrix (FIM)and the posterior Cramer-Rao lower bound (PCRLB).The inverse of the FIM denotes the PCRLB,both of which provide a performance index for the next optimization process.In fact,traditional optimal methods include linear programming,genetic algorithm,particle swarm optimization,and so on.A new optimal data fusion methodology based on the adaptive fading unscented Kalman filter was presented,which can improve the system adaptability and robustness[13].A sensor management framework with Cramer-Rao bounds and FIM tools was proposed,which efficiently utilizes the limited sensor resources[14].A strategy of determining the sensor path and guiding sensors was developed,which solves the problems of planning time and cost uncertainty[15].

In this paper,we choose a scenario where the airborne multi-sensor system tracks multiple ground targets,and the mobile sensor resources is limited.Considering each unmanned aircraft vehicle(UAV)is equipped with many sensors to provide measurement data,we take each unmanned aircraft as a sensor note.The purpose of multi-sensors placement is to acquire the best estimate of the target information.The decision of deployment time,location,and observable target group for each sensor note is made by a management center,which can be a ground console or the specific UAV.The contribution of this paper is proposing a multi-sensor optimal placement algorithm by using the homogeneous design and regional division.Firstly,real-time status measurement of targets is acquired by using extended Kalman filter (EKF).Then by the primary optimization of sensor placement,we can get the optimal observable group for each sensor.After the quadratic optimization,we can get the optimal real-time position for sensors.Finally,the real-time path planning for each sensor is provided.

1 Problem formulation

In order to track the ground moving targets and obtain an accurate estimate of the target status,airborne multi-sensor should be deployed to the optimal position.However,in the process of multi-sensor optimal placement,there are three interrelated problems that need to be addressed.The first one is the method of assigning the observable target group real-time and deploying the appropriate position for each sensor,which is especially important when sensor resources are limited.The second one is the appropriate time to introduce new sensors,and it is worth noting that the optimal position also needs to be determined.The last one is the optimal guiding path for sensors,which is essentially an optimization problem.

In this paper,we assume that each target moves independently with a constant velocity,and each sensor can provide angle and distance measurement to the management center.In addition,the measurement information is available only when the target is in the coverage of the sensor.

Fig.1 Relative motion between an airborne sensor and targets

The relative motion between an airborne sensor and targets is shown in Fig.1,whereSiandTirespectively denote theith sensor and theith target,andsvki,vkidenote the speed of theith sensor and theith target,respectively.The number of targets is defined asN1,the multi-target system model can be expressed as follows[16]:

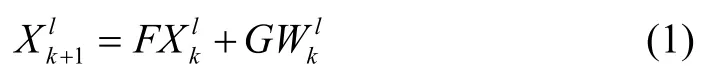
whereFrepresents the state transition matrix,is the state vector of the targetl(l=1,2,…,N1),.Grepresents the noise coefficient matrix,the white noise processobeys a zero-mean Guaussian distribution whose covariance matrix is

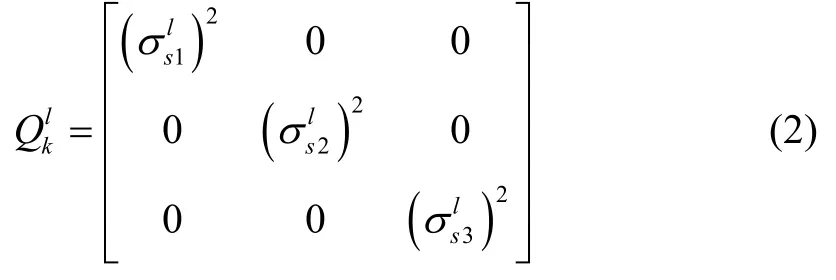
The number of sensors available for dispatching is defined asN2,multi-sensor observation model can be constructed as[15]

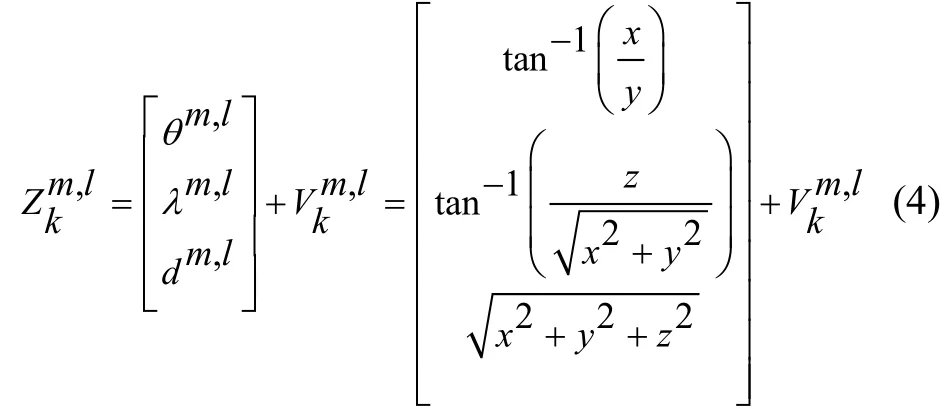
andθm,l,λm,l,dm,ldenote the ballistic inclination,elevation of line of sight,and relative distance of sensor-target,respectively.represents a white noise process,which obeys a zero-mean Guaussian distribution whose covariance matrix is

Note that there is no correlation betweenand.

The main task of multi-sensor cooperative target tracking is to use the measurement data of multiple sensors to track target.Due to the advantages of simple calculation,short running time and good tracking accuracy,EKF is the most widely used filtering method at present,which has been well applied in communication,navigation,control and other fields.In this paper,we adopted EKF to estimate the target state,and the measurement update steps of EKF are as follows[18].

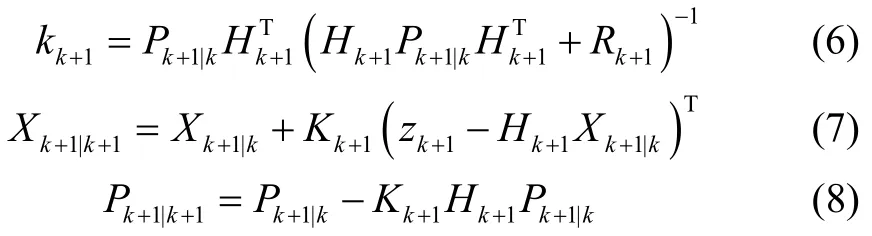
where H denotes Jacobian matrix of Eq (3),and

2 Multi-sensor optimal placement algorithm

Due to the number of sensors and their search range are limited,it’s significant to maximize the benefits of each sensor for searching targets.However,there is little literature currently considering limited mobile sensor management for multiple-target-tracking environment.Our main motivation lies on the desire to develop a feasible multi-sensor placement algorithm to address the problems of limited mobile sensor management for multi-target tracking.In this section,a multi-sensor optimal placement algorithm based on the homogeneous design and regional division is developed,which has better real-time capability and target tracking accuracy.

The block diagram of the proposed algorithm is shown in Fig.2.

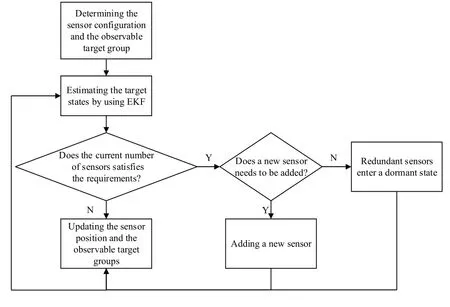
Fig.2 The block diagram of the proposed algorithm

The rule is that every time a new measure is reached,a loop is executed.The detailed process is described as follows: at the initial moment,the sensor configuration and the assignment of the observable target group are determined by system.Then,the extended Kalman filter(EKF)is used to estimate target states and calculate whether the current number of sensors satisfies the requirement.Obviously,there is a classification process,that is,if the number of sensors is insufficient,a new sensor will be added.On the contrary,if the number of sensors exceeds our needs,redundant sensors will enter a dormant state.Finally,the system will update the sensor position and the observable target group,and provide an optimal path planning of sensors.

2.1 The primary optimization of sensor placement

Based on statistical knowledge,there are 2N-1 target groups forNtargets.In order to determine the optimal observable target group for each sensor,the problem of the primary optimization is expressed as follows.

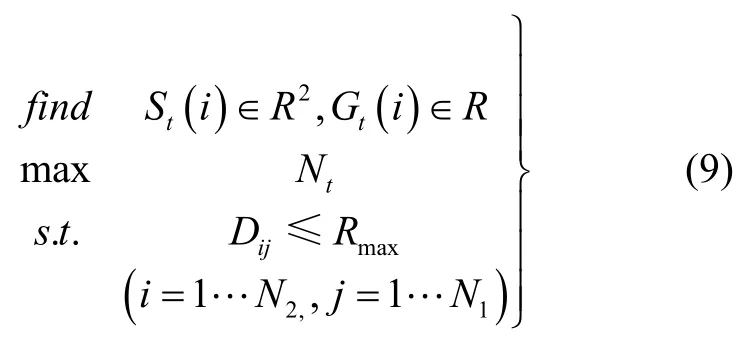
whereSt（i）andGt（i）denote the position and the observable target group of sensori,respectively.Ntis the number of the observable targets of each sensor.We assume that each sensor has the same detection radius,Rmaxis the largest detection radius,Dijdenotes the distance between sensoriand targetj,N2denotes the number of sensors,respectively.

We can solve this problem by adopting enumeration method,random search method,generalized descent method,and so on.In this paper,we use the method of the homogeneous design and regional division.We assume that each target can only be detected by one sensor,and the information acquired by other sensors will be discarded.The detailed process is as follows.

Firstly,we need to acquire the feasible region of sensor position based on the data of management center,and the feasible region isx∈［xmin,xmax］,y∈［ymin,ymax］.The expression is as follows.

By the method of the homogeneous design,a series of points （P（q）,q=1,…,Q）are evenly distributed in the feasible region,which is characterized by uniform dispersion,andQdenotes the number of points in feasible region.

TakingP(q)as the initial point of calculation,namely,St（i）=P（q）.Calculating the maximum value ofNt,then the global optimal solution of the optimization problem (9)can be obtained,which can be described as

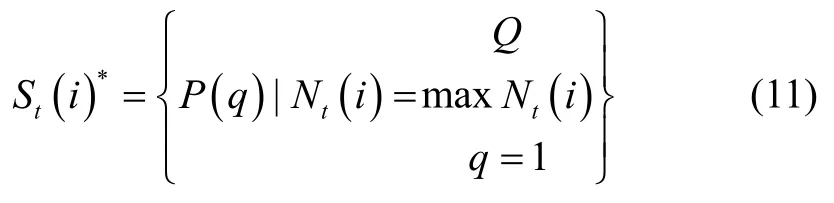
Then,we can obtain the optimal observable target groupGt（i）of sensori.In fact,the position of sensors is real-time updated,and the position of sensors at this time may not be suitable for the next time.So we should calculate the optimal position based on each measurement.

Finally,the regional division method is used to divide the observation range of each sensor into a safe zone and a dangerous zone,as shown in Fig.3.When all targets in the target group of sensoriare in the safe zone,we will not update the position of sensoriat the current time,and vice versa.Therefore,each sensor can track the corresponding target group when moving to the optimal position.

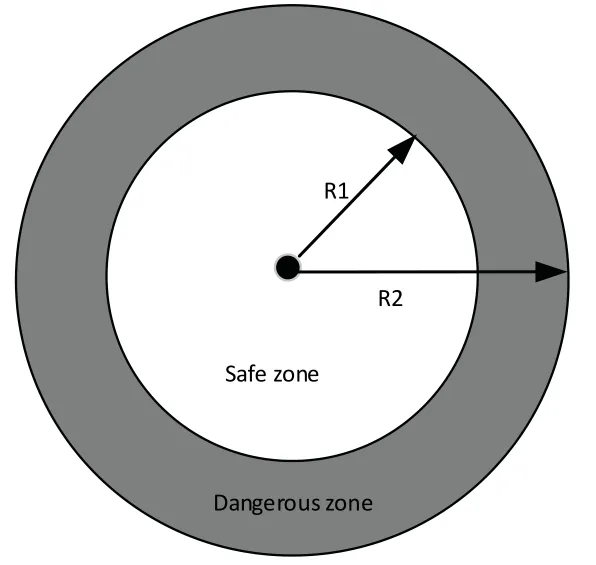
Fig.3 Regional division diagram

2.2 The quadratic optimization of sensor placement

In this section,we can further reduce the feasible area of each sensor based on the above algorithm,and the new feasible region isx∈[xmin′,xmax′],y∈[ymin′,ymax′],

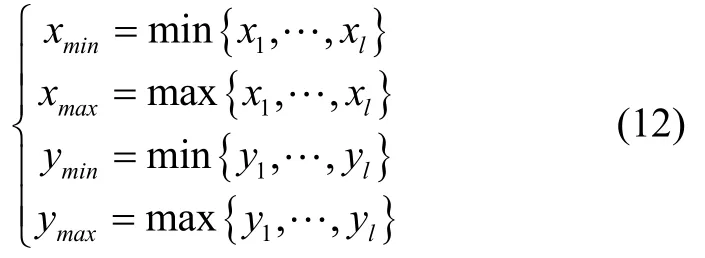
wherel∈Gt（i）,andxl,ylare the horizontal ordinate and longitudinal coordinate of the target position in the target groupGt（i）,respectively.

Then,the optimization problem (9)can be rewritten as

whereαi=[Di1,…,Dij]T,j∈Gt（i）.

The optimal solution can be calculated in the new feasible region.Note that the regional division method is still used in this section,the detailed description can be seen in the previous section.

2.3 The path planning of sensors

In the previous two sections,the real-time optimal position of sensors is given,but the homogeneous design searches the optimal sensor position by column.We use the symbolito label sensors,but the label of each sensor only depends on the occurrence order of the sensor in the process of searching the position by the column.Therefore,for each sensor,its label is not inherited,which makes the path points of the sensors of the same label intermittent.

Obviously,the results obtained by the above algorithm cannot be directly used for the motion control of the sensor,so we need to deal with it further.When the new position points of sensors are acquired,we need to match them to the position points of sensors of the previous moment.So the matching conditions are constructed as follows.If the conditions are met,they are considered to be the path points of the same sensor,and vice versa.

Therefore,we will get the following several situations:

a.Ifkt＜kt-1,it means that the number of required sensors at timetis decreased,then redundant sensors will enter a dormant state.

b.Ifkt＞kt-1,it means that the number of required sensors at timetis increased,then we need to add a new sensor.

c.If the number of matched sensors at timetis less than the number of sensors we needed,we will also need to add a new sensor.

3 Numerical simulation

Considering the number of ground targetsN1=10,the maximum number of sensorsN2=6.The initial location of targets can be seen in Tab.1.

Tab.1 The initial location of targets

The initial velocity vector of each target follows a uniform distribution on the interval from 0 to 10 m/s,the parameters of the noise covariance are［σ1,σ2,σ3］=0.1*[1,2,1],［ρ1,ρ2,ρ3］=0.01*[5,5,6],respectively.

The primary position and the observable target group of sensors are shown in Fig.4,which are obtained by the primary optimization algorithm.In addition,the observable target groups ｛5,6,7,8｝,｛3,4｝,and ｛1,2｝belong to the sensor 1,2,and 3,respectively.

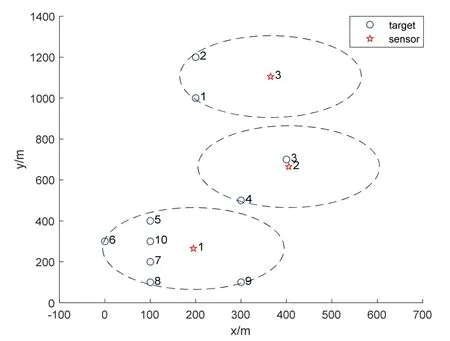
Fig.4 The primary optimal placement of sensors at the initial time

The results of the quadratic optimization algorithm are shown in Fig.5,which clearly shows a more suitable location of each sensor,and compared with the primary optimization algorithm,it is not be easy to lose targets when they move.In order to further illustrate this conclusion,a small experiment is carried out,that is,let targets move randomly and sensors are fixed,then the number of lost targets by each sensor in a period of time is shown in Tab.2.

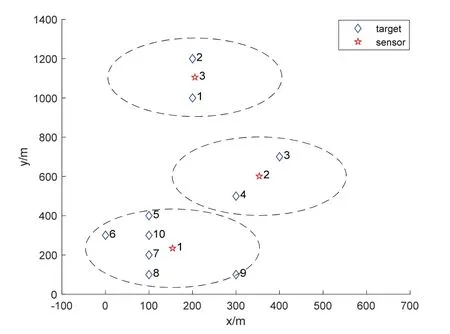
Fig.5 The quadratic optimal placement of sensors at the initial time

Tab.2 Comparative experiment results of the number of lost targets

The track points of sensors that was initially obtained within 700 seconds are shown in Fig.6.The label next to the line indicates the serial number of the trajectory and current time.Note that the trajectory of the same sensor splits into multiple line,because the labels of sensors are not inherited in time,just as we mentioned above.And we can also conclude that the maximum number of required sensors is 5,which satisfies the condition.

The track points of sensors obtained after the matching process are shown in Fig.7,it’s noting that only 3 sensors are used from 1 to 11 seconds,4 sensors are used from 12 to 29 seconds and 4 sensors are used from 50 to 60 seconds.The real-time change of the number of sensors is determined by the path planning strategy which we proposed above,and the maximum number of required sensors is 4.Moreover,the trajectory of mobile sensors in Fig.7 is better than Fig.6.

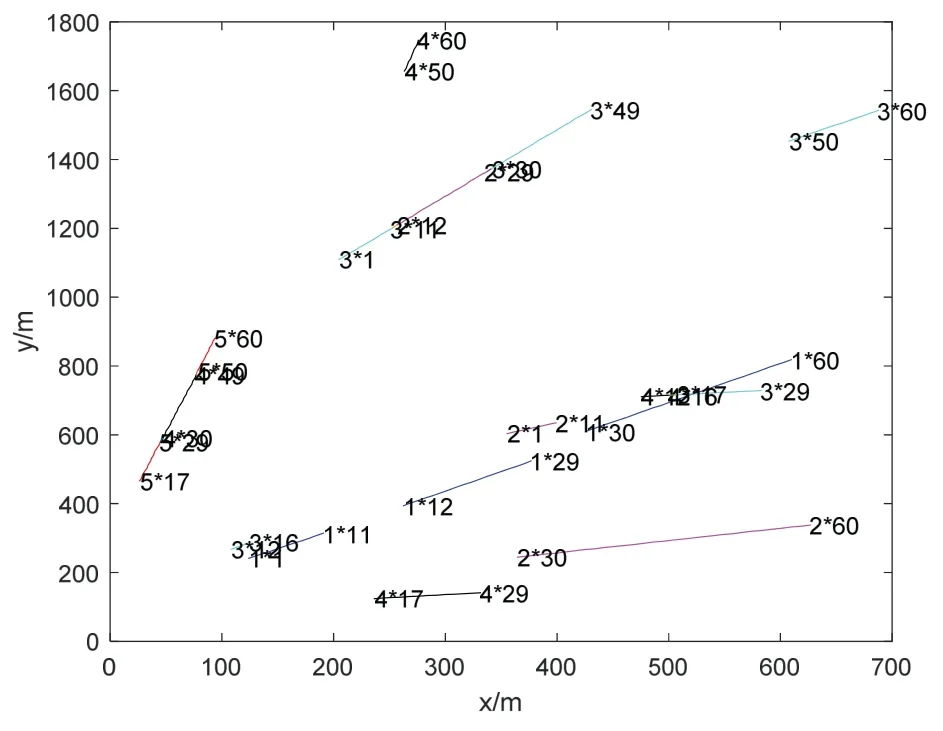
Fig.6 The track points of sensors

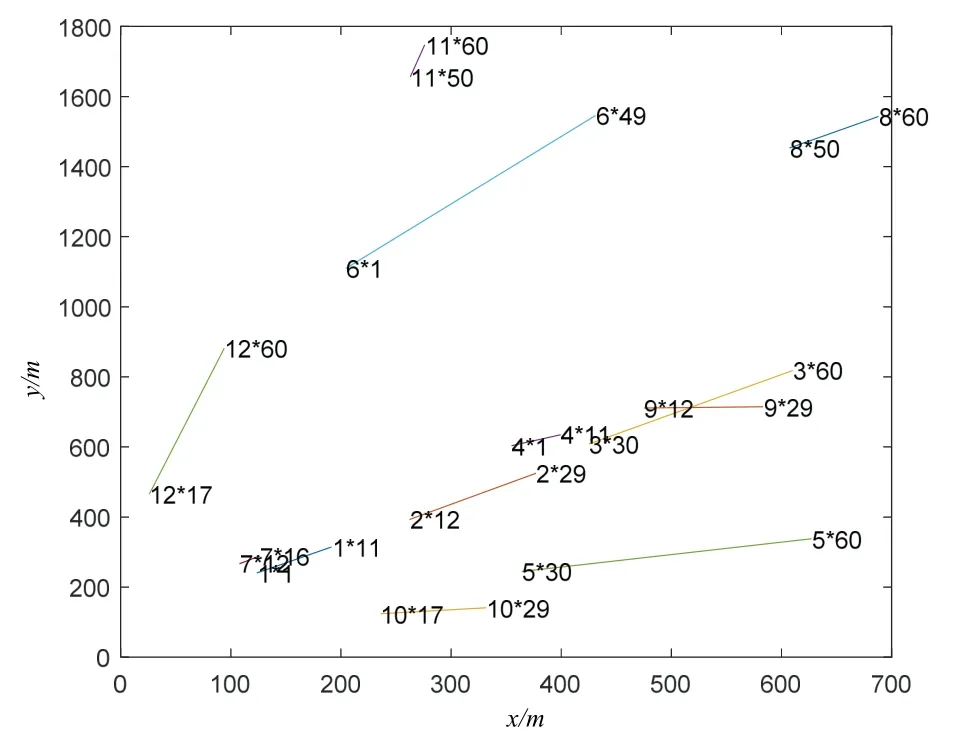
Fig.7 The track points of sensors after the matching process

4 Conclusion

This paper researches the problem of deploying limited sensor resources to track multiple ground targets,and a multi-sensor optimal placement algorithm based on the homogeneous design and regional division is proposed.The proposed algorithm can determine the optimal configuration and the observable target group for each sensor,and guide them to track the moving targets in an optimal way.Several simulation results are given to verify the feasibility of the proposed algorithm.Compared with the primary optimization,the quadratic optimization can obtain more suitable sensor location which is not easy to be lost targets when they move,and save the limited sensor resources.Therefore,the proposed algorithm in this paper is a powerful tool for multi-sensor management,which can be considered as a stepping stone to be used towards the development of multi-sensor placement problem.