一种大安装偏差快速传递对准中的闭环卡尔曼滤波算法
李寿鹏,穆荣军,崔乃刚,龙 腾
(哈尔滨工业大学 航天学院,哈尔滨 150001)
机载导弹发射前,弹载低精度子惯导以机载高精度主惯导作为位姿基准,通过动基座传递对准技术快速获取准确初始状态。由于发射架与机翼、导弹间的安装方式以及机翼形变等原因,主子惯导间比较容易产生较大的安装偏差,导致惯导姿态与速度误差模型的非线性增强,如果仍采用KF 算法,则会因模型线性化误差而导致滤波器估计精度下降。
当前解决该问题的思路基本有两种,一类是建立非线性系统模型,采用非线性滤波算法[1],另一类是将非线性系统转化或近似为线性[2],依然采用线性最优的KF 算法。从非线性系统角度考虑该问题,采用的非线性滤波算法包括UKF[3]、容积卡尔曼滤波(Cubature Kalman Filter,CKF)[4]、粒子滤波(Particle Filter,PF)[5]等,但非线性滤波器计算量较大的问题是影响实时性的主要因素,因此一些算法根据具体模型,在不损失精度的前提下对非线性滤波器进行改进或简化,如简化UKF[2],简化高阶CKF[6]等。
当从线性角度考虑该问题时,研究重点则集中于如何将非线性系统转化为线性系统以适应KF 算法框架。典型的是采用扩展卡尔曼滤波器(Extended Kalman Filter,EKF),通过泰勒展开将非线性系统线性化,但由于EKF 算法仅保留了一阶项,在系统非线性较强时会产生难以忽略的高阶截断误差,可以通过保留高阶项来弥补该缺点,如二阶EKF[7]。文献[8]基于加性四元数推导出线性的姿态误差模型,但是速度误差模型依然无法摆脱非线性。
系统线性化的另一个思路是首先粗略估计出子惯导姿态误差并补偿,使其满足小角度假设,然后在此基础上采用线性传递对准模型和KF 完成姿态误差的精确估计。文献[9]采用数秒子惯导数据粗略算出水平姿态,来构造与子惯导姿态接近的虚拟主惯导,作为后续对准过程中的子惯导姿态基准;文献[10]则首先通过线性模型估计出姿态误差,补偿后再采用相同的模型进行二次精确估计,但需要存储数秒主子惯导数据。
针对以上问题,通过对非线性模型的线性化过程进行详细分析,得出姿态误差高阶耦合项将导致线性滤波器的估计精度下降。采用安装角估计值和主惯导姿态共同建立子惯导姿态基准,使子惯导姿态与基准之间的安装关系满足小角度假设,从而可以继续使用KF 算法。
在传递对准过程中,为使系统始终保持良好的线性状态,设计了一种反馈校正机制,即在每次量测更新后,修正主子惯导间的安装角估计值、子惯导解算出的状态量以及陀螺仪零偏估计值,使所建立的子惯导基准系与子惯导状态逐渐逼近实际状态,并采用陀螺仪零偏估计值对子惯导输出数据进行补偿,然后再进行子惯导状态解算,以延缓其姿态发散的速度。通过仿真实验与对比分析,表明了所设计的闭环卡尔曼滤波器(Closed Loop Kalman Filter,CLKF)在几乎不增加计算量的前提下,有效地提高了线性滤波器的估计精度,并消除了系统非线性对传递对准的影响,具有一定的工程实用性。
1 坐标系定义
本文所涉及到的坐标系定义如下:地心惯性坐标系i;地心地固坐标系e;选择“东-北-天”地理坐标系为导航系n;选择载体的“右-前-上”坐标系为载体系b;主惯导载体系记作m;子惯导标称载体系、计算载体系和实际载体系分别记作、s*和s;由安装矩阵估计值和主惯导姿态矩阵构建子惯导姿态基准矩阵,其中系即为子惯导基准载体系;各载体系间的关系如图1所示,s˜系与m系间的姿态误差定义为安装角ψa,s系与s˜系间的姿态误差定义为挠曲变形角θf,s*系与m系间的姿态误差定义为载体系失准角ψm,系与m系间的姿态误差为载体系失准角估计值。

图1 不同载体系关系图Fig.1 Diagram of different body frames
n系按照Z(ψ)→X(θ)→Y(γ)的转序旋转至b系,则n系与b系之间的姿态转换矩阵为

式中:ψ为航向角;θ为俯仰角;γ为滚转角;s、c分别为正、余弦函数。
2 传递对准模型
2.1 机翼挠曲变形模型
机翼挠曲变形通常采用白噪声驱动的二阶马尔可夫过程来描述,具体为[11]

式中:θfi为挠曲变形角,相应方差为σi;ηi为高斯白噪声,相应的功率谱密度为Qηi;βi为常数;σi,Qηi和βi间的关系为Qηi=4βi3σi2;随机过程相关时间τi与βi间的关系为βi=2.146τi。
2.1 非线性模型
常用快速传递对准状态模型有两种:导航系失准角模型[12]和载体系失准角模型[13],在小角度假设下,文献[14]详细地证明了两种模型的等价性,且基于载体系失准角的传递对准模型的量测向量构造较为简单,量测方程为线性的,因此本文采用载体系失准角模型。
根据文献[6]的相关推导,并考虑惯性器件输出的角速度和加速度包含误差,其中仅考虑陀螺仪和加速度计的常值零偏,并忽略动态杆臂误差,则可以获得捷联惯导姿态与速度误差非线性模型为


式中:为子惯导陀螺仪输出;为子惯导姿态矩阵的转置,即
2.1.1 状态模型
由于加速度计零偏可观测度较低,在短时间内很难完成估计,因此在传递对准过程中不对该量进行估计。综合考虑“速度+姿态”匹配模型的可观测性和惯性器件常值误差,分别选取子惯导载体系失准角ψm,子惯导速度误差δVn,子惯导陀螺仪常值零偏εs,安装角ψa,挠曲变形角θf以及变形角速度ωf作为状态向量X,即
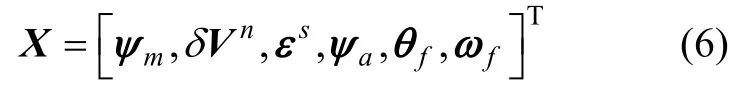
在主子惯导间安装偏差较大的情况下,载体系失准角ψm以及安装角ψa不满足小角度假设,且载体系失准角矩阵、安装角矩阵与的转换顺序类似,挠曲变形角θf满足小角度假设,则满足,其中向量ψ的反对称矩阵ψ×的具体形式为

在对准期间认为陀螺仪零偏和安装角保持不变,根据式(2)(3)(4)(5),且忽略小量以及,则可得传递对准非线性状态模型的矢量形式为
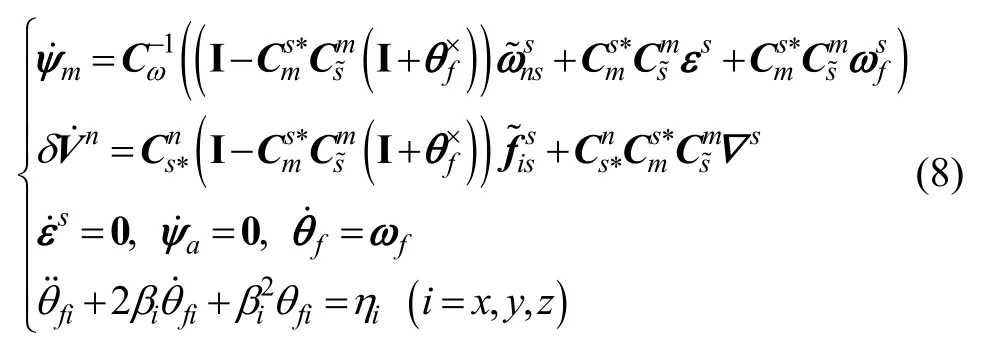
2.1.2 量测模型
选取子惯导载体系失准角和主子惯导间的速度之差作为量测向量Z,即



式中:为主惯导姿态矩阵。
由此可得传递对准观测方程为

式中:V为量测噪声;H为量测矩阵,具体形式为
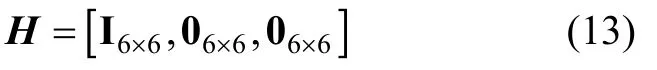
式中: I6×6为6 阶单位矩阵; 06×6为6 阶零矩阵。
2.2 线性模型
2.2.1 状态模型
线性模型采用与非线性模型相同的状态向量,如式(6)所示,且在安装偏差较小的情况下,载体系失准角和安装角满足小角度假设,即和,且根据式(4)可得的近似形式为

将上述近似关系代入传递对准非线性模型式(8)中,且忽略二阶及以上小量,可获得传递对准线性状态模型矢量形式如下

2.2.2 量测模型
线性模型采用与非线性模型相同的量测向量,如式(9)所示,但求取载体系失准角量测值的方式略有不同,具体为:

2.3 模型线性化误差分析
“速度+姿态”匹配快速传递对准一般在匀速平飞阶段通过速度观测完成水平姿态的估计,而在滚转机动阶段通过姿态观测完成航向姿态的估计。因此,以下分别就匀速平飞条件下的速度通道和滚转机动条件下的姿态通道展开分析。
当安装偏差较大时,与导航系至载体系的转动过程类似,姿态误差欧拉角按照Z→X→Y的转序,根据式(1)可以得到子惯导计算载体系s*与主惯导载体系m之间的转换关系,如式(17)所示。采用泰勒公式将式(17)中的正、余弦函数展开,并保留二阶及以下项,则可以得到近似关系为sinψ≈ψ和,利用该近似关系将姿态误差矩阵展开,并忽略二阶以上小量(不包括二阶),可得近似关系如式(18)所示。

标称载体系与主惯导载体系m之间的转换关系及其近似关系分别与式(17)(18)类似,只需将其中失准角的下标m换作a即可,不再赘述。将和的近似关系代入式(8)中的速度误差非线性模型,忽略二阶以上小量(不包括二阶)以及次要项,整理可得

式中:δC为由载体失准角矩阵和安装角矩阵线性化引起的姿态误差矩阵,具体形式为

当载机处于匀速平飞状态时,子惯导水平两轴加速度计与垂直轴相比所敏感的比力属于小量,垂直轴加速度计的比力接近重力加速度,则加速度计输出可近似为

式中:g为重力加速度。
因为载机水平姿态角为小量,可近似认为姿态中仅存在航向角,则子惯导姿态矩阵可近似为:
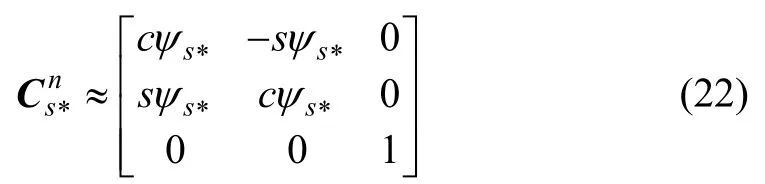
式中:ψs*为子惯导航向角。
将式(7)(20)(21)(22)代入式(19)中,并忽略小量(ψa-ψm)×,展开可得如下关系

从式(23)前两分量可以看出,在水平速度误差模型中,航向与水平姿态误差相互耦合的二阶项,经过重力加速度的放大而引起相对较大的输入偏差,且认为短时间内加速度计零偏较难估计,则该偏差量与加速度计零偏在水平轴上的等效分量共同影响水平两轴安装角的估计精度。

由式(24)可以看出,姿态矩阵线性化误差与陀螺仪零偏相互耦合而产生输入偏差,但由于εs为小量,使得该耦合偏差较小,因此对εs的估计精度影响有限。
当载体处于姿态机动的状态时,其载体系相对导航系的旋转角速度满足,将和的近似关系代入式(8)中的姿态误差非线性模型,为突出线性化误差对姿态误差估计的影响,此处忽略陀螺仪零偏相关项,则可获得如下关系
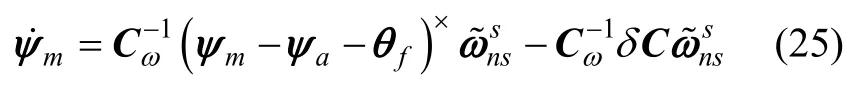
在“速度+姿态”匹配传递对准模型中,载体一般采用摇翼机动的方式来激励航向通道快速收敛,且由于导航系相对惯性系的旋转角速度为小量,可近似认为载体系相对导航系的旋转角速度仅沿滚转轴方向存在分量,则陀螺仪输出可近似为


将式(7)(20)(26)代入式(25)中并展开,整理可得式(27)所示的关系从该式可以看出,依赖小角度假设的线性化方式,会忽略姿态误差角的高阶耦合项,该误差项与载机滚转角速度相耦合而引起载体失准角模型的输入偏差,该偏差量会对俯仰轴与航向轴安装角的估计精度产生影响。
2.4 线性化误差对卡尔曼滤波器的影响
由2.3 节的分析可以看出,当主子惯导之间的安装偏差较大时,仍然按照小角度假设来获得传递对准线性化系统,将使状态模型产生输入偏差,而量测模型始终为线性,则不存在线性化误差。传递对准过程中卡尔曼滤波器需根据系统离散模型不断递推完成相应状态估计,且根据之前的分析,则建立仅状态模型含有输入偏差的离散系统模型,具体如下:
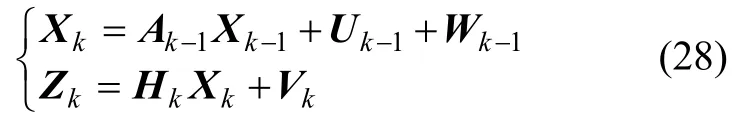
式中:Ak-1为状态转移矩阵,Uk-1为输入偏差,Wk、Vk分别为过程噪声和量测噪声,满足零均值高斯分布,即

式中:Qk为过程噪声方差阵;Rk为量测噪声方差阵。
定义先验与后验估计误差为:
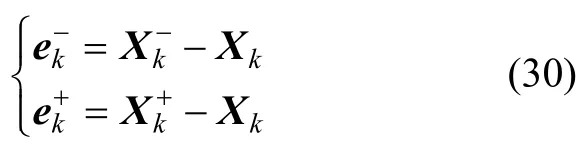
式中:、分别为先验估计及其误差;、分别为后验估计及其误差;Xk为状态量实际值。
根据卡尔曼滤波方程和系统模型,可以获得先验和后验估计误差传播方程为:

式中:Kk为卡尔曼滤波增益矩阵。
由上式可以获得估计误差均值的传播方程为

可以看出,系统的输入偏差Uk-1在每次滤波器时间更新阶段会产生额外的累积偏差-Uk-1,在每次滤波器量测更新阶段会产生额外的累积偏差- (I-KkHk)Uk-1,从而使得卡尔曼滤波器的后验估计有偏。
3 快速传递对准闭环卡尔曼滤波器设计
本文所设计的基于CLKF 的传递对准算法,其主要思想是不直接以主惯导姿态作为子惯导姿态基准,而是寻找一个更接近子惯导姿态的基准,可以保持子惯导姿态与该基准间的姿态误差始终满足小角度假设,此时KF 的估计仍为线性最优,从而避免了使用计算量较大的非线性滤波器,并采用闭环反馈方式来维护系统的线性状态,使子惯导初始姿态逐渐逼近实际值,传递对准流程如图2所示。

图2 基于CLKF 的快速传递对准流程图Fig.2 Flow chart of rapid transfer alignment based on CLKF
具体描述如下:
第1 步:系统初始化
系统初始化主要包括子惯导解算和传递对准滤波器初始化,采用主惯导数据直接对子惯导进行初始状态装订,滤波器状态向量及其协方差阵初始化X0、P0,一般情况下X0=0,即将安装角矩阵和载体系失准角矩阵初始化为
第2 步:子惯导状态解算
当k时刻子惯导IMU 数据更新后,采用k- 1时刻陀螺仪零偏估计值εk-1对角速度测量值进行补偿,采用零偏补偿后的IMU 数据进行子惯导位姿解算,由此获得k时刻解算出的子惯导姿态和速度;
第3 步:滤波器时间更新
采用零偏补偿后的IMU 数据和子惯导解算出的姿态和速度进行滤波器时间更新,即
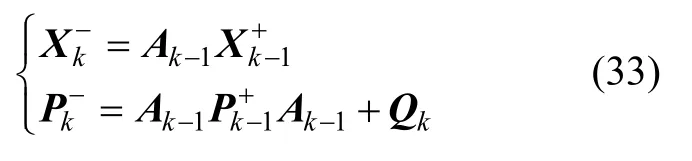
当主惯导数据未更新时,则返回第2 步继续进行子惯导位姿解算和滤波器时间更新,此时不采用滤波器状态对子惯导位姿和陀螺仪零偏进行修正;
第4 步:滤波器量测更新
当k时刻主惯导姿态和速度更新后,则进行滤波器量测更新,由k- 1时刻安装矩阵估计值来补偿,以构造子惯导姿态基准矩阵即为构造的子惯导基准载体系,然后采用构造滤波器量测向量Zk中的失准角部分,即
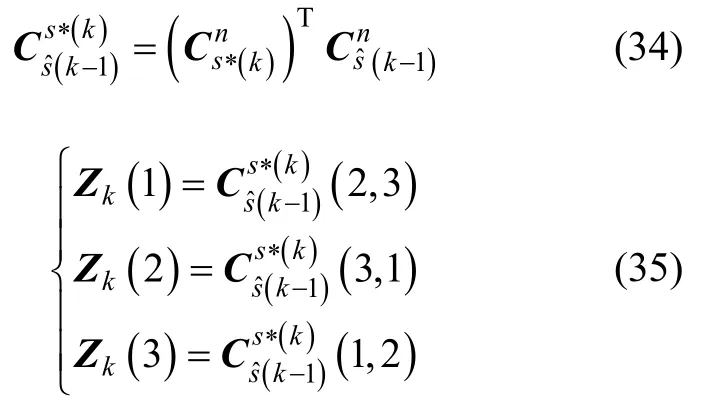
量测向量的速度误差部分仍按照式(9)的方式构造,即取子惯导与主惯导间的速度之差。
在此基础上完成量测更新,即

第5 步:子惯导状态修正
该反馈校正算法在滤波器量测更新后,将对估计出的各项误差量进行修正,由此可以得出,每次滤波器的更新量都是在之前估计值基础上的增量,而非该量的实际估计值。
k时刻由滤波器量测更新所获得的状态向量,包括载体系失准角增量Δψm(k)、安装角增量Δψa(k)、速度误差增量和陀螺仪零偏增量Δεk。由Δψm(k)、Δψa(k)分别构造k时刻子惯导标称载体系、计算载体系与基准载体系之间的矩阵估计值,并采用与Δεk对当前子惯导解算出的姿态与速度、陀螺仪零偏估计值εk-1以及安装矩阵估计值进行修正,具体为

在量测更新与修正步骤完成后,将滤波器状态向量中ψm、δVn、εs、ψa置零,并以修正后的子惯导状态作为初值进行惯导解算。
4 仿真验证与分析
4.1 仿真条件
仿真时间为45 s,载机飞行轨迹可划分为三个阶段,分别为:首先匀速平飞10 s,巡航速度200 m/s,然后摇翼机动10 s,滚转角速度5 °/s,最后采用相同的速度匀速平飞25 s。主子惯导载体系间预设安装角为ψa=[8 °,8 °,8 °],机翼挠曲变形角的标准差分别为σ=[15′,20′,5′],二阶马尔可夫过程的相关时间分别为τ=[5s,5s,10s]。主子惯导器件指标分别为:光纤主惯导,更新频率100Hz,陀螺仪零偏0.01 ° h,随机游走系数,加速度计零偏0.05mg,随机游走系数;MEMS 子惯导,更新频率200Hz,陀螺仪零偏0.02 ° s,随机游走系数,加速度计零偏3mg,随机游走系数
4.2 不同算法对比仿真与分析
采用不同算法在相同的条件下进行仿真,将KF、UKF 和CLKF 算法进行对比分析,不同滤波算法的安装角和陀螺仪零偏估计误差曲线如图3与图4所示。

图3 不同算法的安装角估计误差Fig.3 Estimation errors of physical misalignment angles from different algorithms


表1 安装角与陀螺仪零偏估计误差Tab.1 Estimation errors of physical misalignment angles and gyro biases
相应的估计误差值如表1所示,挠曲变形角和角速度估计值曲线如图5与图6所示,相应的估计误差值如表2所示。

图5 不同算法的挠曲变形角估计值Fig.5 Estimation values of flexure deformation angles from different algorithms


表2 挠曲变形角与角速度估计误差Tab.2 Estimation errors of flexure deformation angles and angular velocities
根据上述仿真结果,由图3和表1可以看出,CLKF 算法在水平安装角估计精度上与UKF 算法相当,在航向安装误差角的估计精度上稍优于UKF 算法,且明显优于KF 算法,表明CLKF 算法可以有效地补偿航向与水平姿态误差角的高阶耦合项对线性卡尔曼滤波器估计精度的影响,在安装角估计收敛速度方面,水平通道基本在载机平飞阶段即可收敛,而航向通道则在开始摇翼机动后的5 s 时收敛,算法快速性可以满足要求;由图4和表1可以看出,不同算法在陀螺仪常值零偏的估计精度与收敛速度方面基本相当,表明模型线性化误差对该项的估计影响较小;由图5、图6和表2可以看出,在对机翼挠曲变形角与角速度的估计方面,不同算法都可以实现机翼挠曲变形角与角速度的跟踪,且估计精度与收敛速度也基本相当,水平通道在10 s 内收敛,而航向通道在15 s 内收敛。
为对比不同算法的计算量,统计不同算法在整个传递对准周期内,调用滤波器和整个程序的计算耗时,如表3所示,其中,仿真软件采用Matlab2016b,计算机处理器为Intel Core i7-4790。从算法耗时的统计结果上可以看出:CLKF 算法的滤波器耗时与KF 较为接近且约为0.5 s,而UKF 算法的滤波器耗时则约为17.4 s,可见CLKF 的计算量与KF 相当,仅为UKF的3%,所设计的算法在保持估计精度的同时,可以有效地降低计算量。

表3 不同滤波器与总程序耗时Tab.3 Elapsed time of different filters and entire programs
5 结 论
通过对传递对准非线性模型线性化误差的分析以及不同滤波算法的对比仿真,可以得出以下结论:
1)航向与水平姿态误差角的高阶耦合项经重力加速度的放大,对水平安装角的估计精度产生较大影响,而姿态误差角的高阶耦合项经摇翼机动角速度的放大,对航向安装角的估计精度产生影响,该耦合误差与小量零偏项耦合对陀螺仪零偏的估计精度影响较弱;
2)CLKF 算法可以有效地补偿模型线性化误差对线性KF 的影响,其估计精度优于KF 且与UKF 相当;
3)在滤波器收敛速度方面,CLKF 算法与KF、UKF 相当,可以满足传递对准对算法快速性的要求;
4)CLKF 算法在保持估计精度的同时,计算量与KF 相当,仅为UKF 的3%,有效地降低了计算量。

