基于非机动窗口捕捉的陀螺漂移在线补偿方法

王海涌，徐 源，王伟东，刘佳琪

（1.北京航空航天大学宇航学院，北京 100191; 2.北京航天长征飞行器研究所，北京 100076）

地磁导航具有自主性、无积累误差的优点，与捷联惯导组合依然保持导航自主性[1-4]。但不同高度区域的磁场环境复杂，需在应用区域建立精确的地磁场模型。

利用加速度计、磁强计获得重力矢量和地磁矢量修正姿态误差的方法受到广泛关注[5-11]，但在载体晃动或机动条件下不具适用性。文献[12]则面向动态工况环境，将晃动情形下的有害加速度作为高频噪声，通过互补滤波加以补偿。但其算法中的对姿态误差方程的过分近似和简化处理不合理，引入了额外误差，难以有效提高导航精度。

高动态条件下飞行器导航系统分析和处理技术一直是核心技术和难点，从工程角度考量，机动工况在整个任务过程中的时间占比毕竟很低，绝大部分时段都是非机动工况，如悬停、匀速直航，一枚全导式导弹的中途巡航段大都是非机动工况。本文针对中低精度自主导航需求，提出了一种基于非机动窗口捕捉的姿态误差在线修正方法。基于加速度计输出值判定飞行状态，捕捉非机动窗口，利用地平系下地磁矢量以及重力矢量通过新型滤波方法修正三轴姿态角，以期获得较好的工程实用效果。

1 地磁场模型

地磁场是一个矢量场。比较著名的地磁场模型是每隔5年公布一次的IGRF(International Geomagnetic Reference Field)[4]。地磁场强度势函数V表示为:

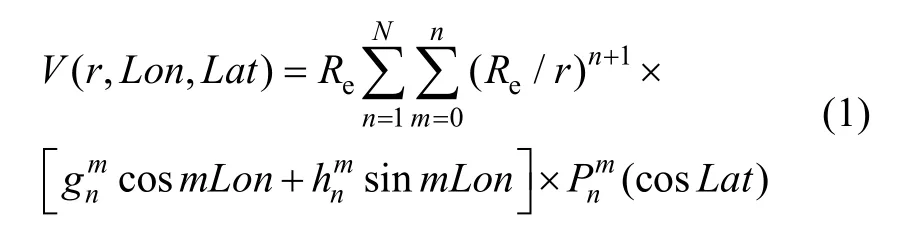
式中:Re为地球半径，r为地心距，Lon为当地地理经度，Lat为当地地理纬度，N为IGRF 模型的截止阶数，本文取N=10；和为高斯系数，由IGRF 模型提供；(cosLat)为施密特准归一化n次m阶Legendre函数。

地磁场强度B在导航系(以东北天地理系为导航系)n 系中的矢量为Bn，在地球坐标系e 系中的矢量为Be，在本体系下的矢量B（b由三轴磁强计测量获得），假定三轴磁强计坐标系与载体坐标系重合，则有如下关系:

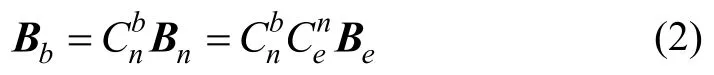
式中:Be通过磁场势函数解算得到[11]。为捷联矩阵，地球系到导航系的转换矩阵可以表示为:

2 捷联惯导/重力/地磁组合系统模型

2.1 系统状态方程

以平台失准角φx,φy,φz（记为列向量φ）和三轴陀螺漂移εx,εy,εz（记为列向量ε）为状态量，建立状态方程:

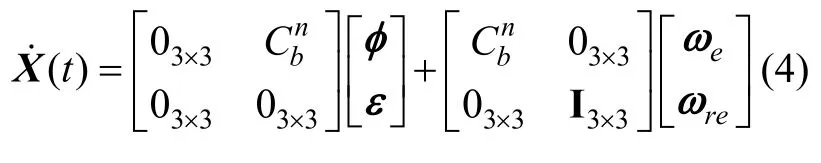
式中为捷联矩阵的转置，ωe，ωre为陀螺随机噪声。

2.2 量测量构建

2.2.1 重力矢量计算水平失准角

加速度计测量值为比力fb。地理系下惯导的比力方程为:

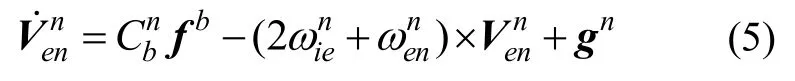
gn为所在高度处的重力加速度，后两项称为有害加速度。当载体悬停或匀速运动时，，此时式(5)可近似为:

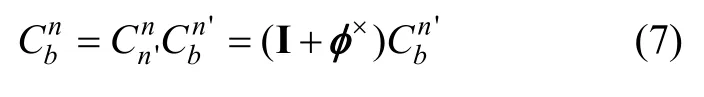
式中，φ×为由φx,φy,φz张成的反对称矩阵:

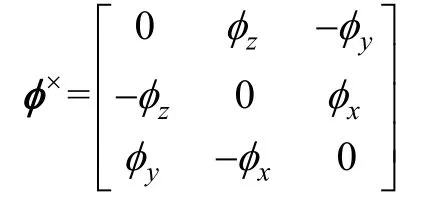
将式(7)带入式(6)得:

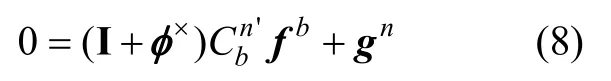
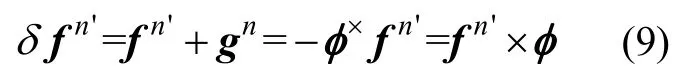
非机动状态时，有fn'=-gn=［0 0g］T。重力矢量作为参考只可估计二维水平失准角φx,φy，则式(9)变为:

2.2.2 基于地磁场水平分量的航向角计算

地磁场矢量B的模为地磁场强度B，B在导航系下分量描述如图1所示:

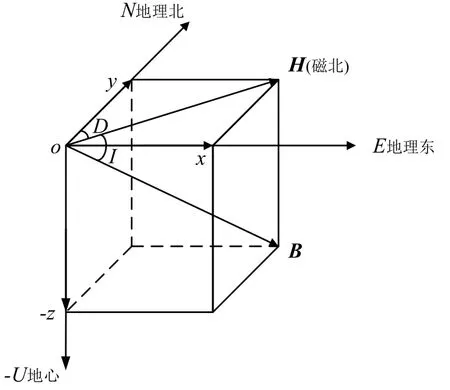
图1 地理坐标系下地磁要素Fig.1 Geomagnetic elements in geographical coordinate system

OENU为导航系，地磁矢量B在水平面OEN上的投影H为水平分量，其模为H。D为磁偏角，B与水平面的夹角I称为磁倾角。

载体的俯仰角、横滚角记为φ、γ，由312 转序可得捷联矩阵:

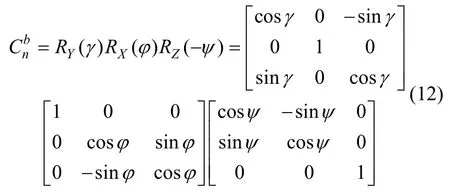
建立地平坐标系h，与本体系b间的转移矩阵为:

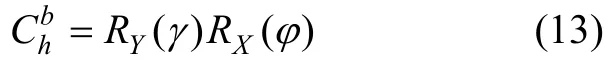
则可求得B在h系下的矢量坐标:

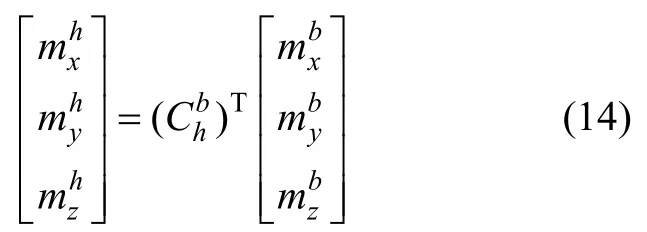
由矢量关系式:

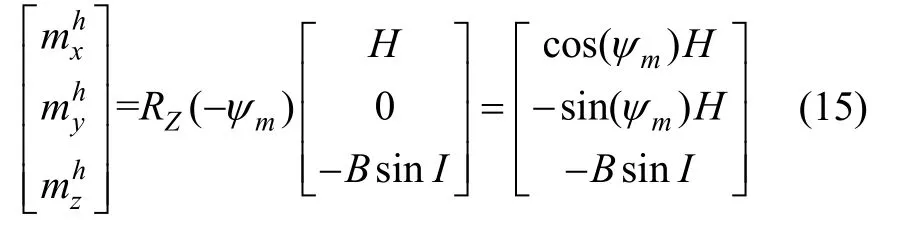
则可求得磁航向角主值ψm:

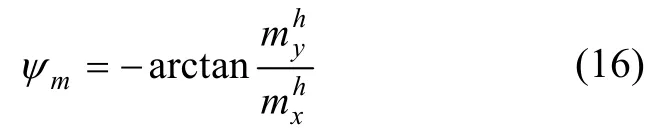
ψm的真值需根据、进一步判断。那么载体的航向角观测量为:

式(13)中的γ、φ现有方法中有二种获得方式:一是将陀螺积分的姿态带入；二是直接利用重力矢量计算[6-12]，如式(18):

本方法将水平失准角与航向失准角先后滤波，先对水平姿态角滤波，再带入到式(13)～(16)求解航向角观测量，可以降低误差干扰提高定姿精度。

2.3 信息融合

采用输出反馈卡尔曼滤波方式，将水平失准角与航向失准角分开滤波，其原理图如图2所示。

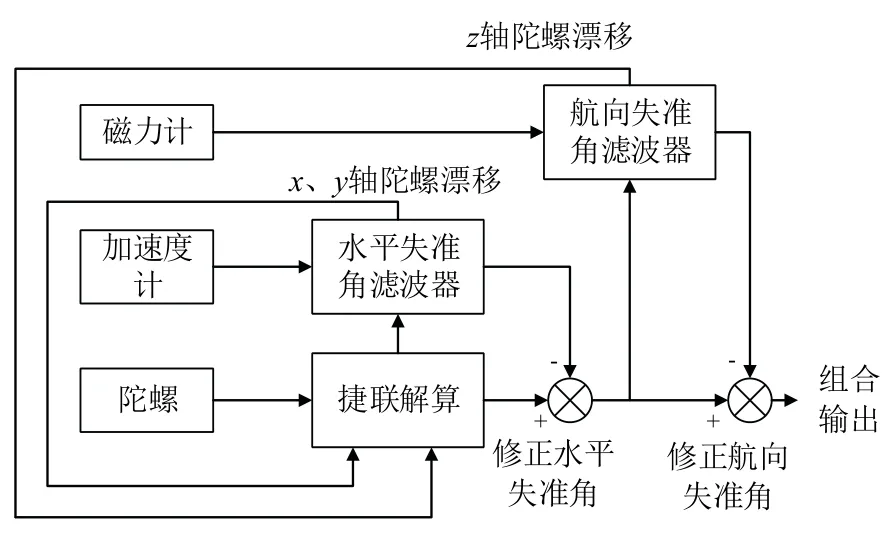
图2 组合导航系统原理图Fig.2 Principle figure of integrated navigation system

2.3.1 水平失准角滤波器

水平失准角滤波器的状态量为X1=[φx φy εx εy εz]T，状态方程为:

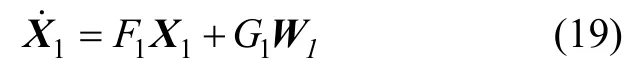
式中W1=[ωex ωeyωrex ωreyωrez]T为陀螺仪噪声。

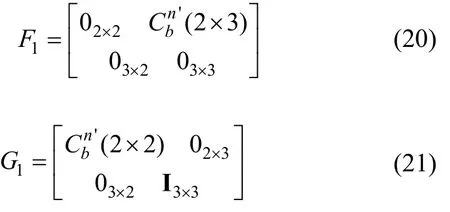
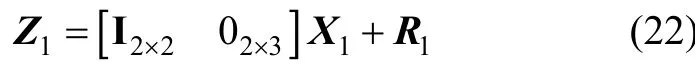
式中R1为水平姿态量测噪声协方差阵。

2.3.2 航向失准角滤波器的设计

根据平台失准角与姿态误差角关系:

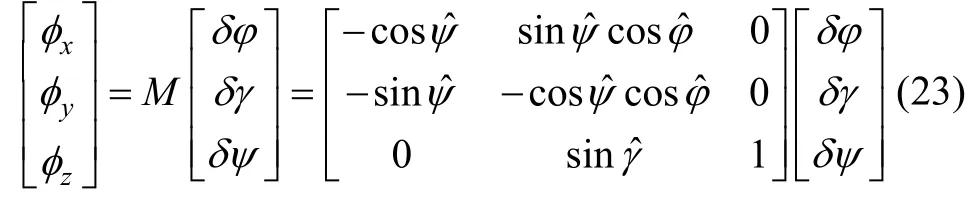
滤波后的水平姿态可认为误差角为0，根据式(20)此时航向失准角与航向误差角相等，则。以φz和本体系下Z轴陀螺漂移εz为状态量的系统模型为:

式中R2为航向量测噪声。

2.3.3 非机动窗口捕捉策略

即便在非机动工况下，加速度计输出值的模|fb|也会因器件噪声及载体晃动等原因围绕重力加速度g在一个区间呈波动状态。加速度计比力随机噪声标准差σax、σay、σaz通过标定测试或者在线获得，令。建立判别指标α，公式如下:

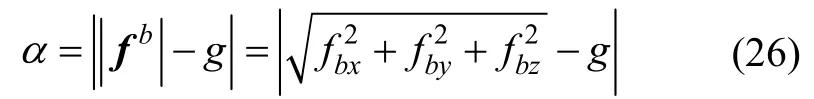
根据α在线实测值进行工况判别方法如下:

(1)非机动飞行:α≤1 0σa，此时判定载体处于非机动飞行状态，式(22)中的R1=[σayσax]T。

(2)低加速度飞行:10σa≤α＜ 30σa；设计比例系数px、py，可以设计为α函数。式(22)中的R1变为如下形式:R1=[py(α)σaypx(α)σax]T，即量测噪声协方差阵随α而改变。

(3)大机动飞行或失重状态:α≥ 30σa，本方法已不再适用，滤波器停止工作。

上述方法中的系数10、30、px(α)和py(α)只是设计阶段的一个例子。随着工程背景或在线实际情况的不同应做相应调整。

3 计算机仿真试验

3.1 仿真条件设置

将飞行仿真轨迹设计为非机动情形(匀速飞行段)和机动情形(起飞爬升段、机动飞行段)的组合，以验证本方法能否捕捉非机动窗口；利用匀速飞行段导航数据评估本方法的陀螺漂移补偿的姿态精度。仿真时间为330 s，捷联惯导全程工作，125 s 后滤波器根据判断条件捕捉非机动窗口进行滤波，300 s 后滤波器停止工作。仿真轨迹如图3所示:

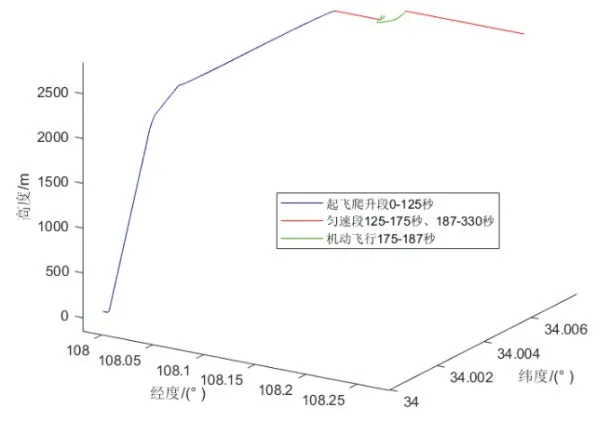
图3 设计的仿真飞行轨迹Fig.3 Designed simulation flight trajectory

仿真环境参数如下:

(1)出发点北纬34 °，东经108 °，海拔高度100 m，仿真过程中最大飞行高度海拔2.73 km。

(2)初始航向角90 °，俯仰角0 °，横滚角0 °；航向失准角1 °，俯仰、横滚失准角0.3 °。

(3)采样周期:陀螺、加速度计采样周期0.01 s，磁力计采样周期0.1 s，惯导解算周期0.01 s，卡尔曼滤波周期0.1 s。

(4)器件参数:陀螺常值漂移6 °/h，随机噪声标准差为0.002 °/s；加速度计常值偏移为10 mg，随机噪声标准差2 mg；磁强计噪声100 nT。

3.2 结果分析

组合导航系统的姿态角误差如图4～6，速度误差如图7所示。

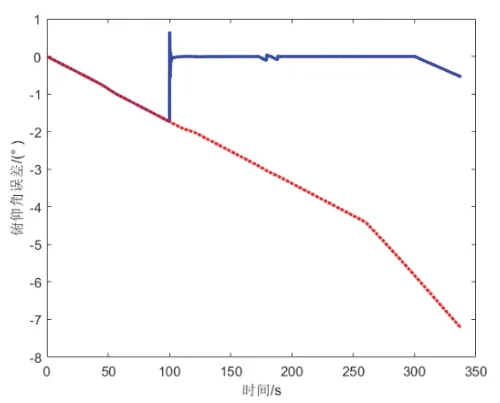
图4 俯仰角误差Fig.4 Pitch angle error

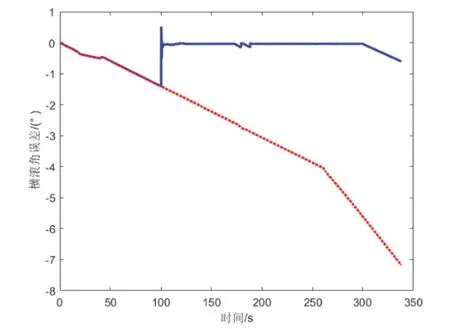
图5 横滚角误差Fig.5 Roll angleerror

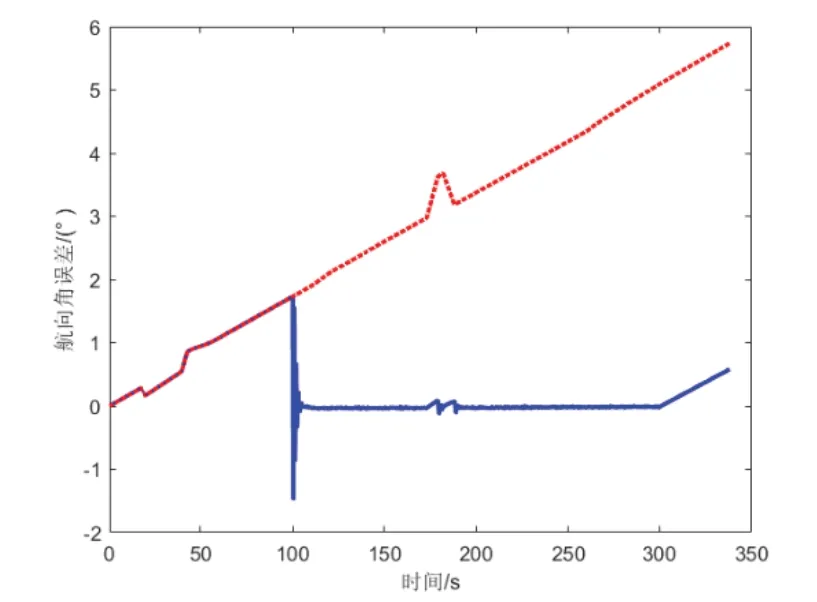
图6 航向角误差Fig.6 Heading angle error

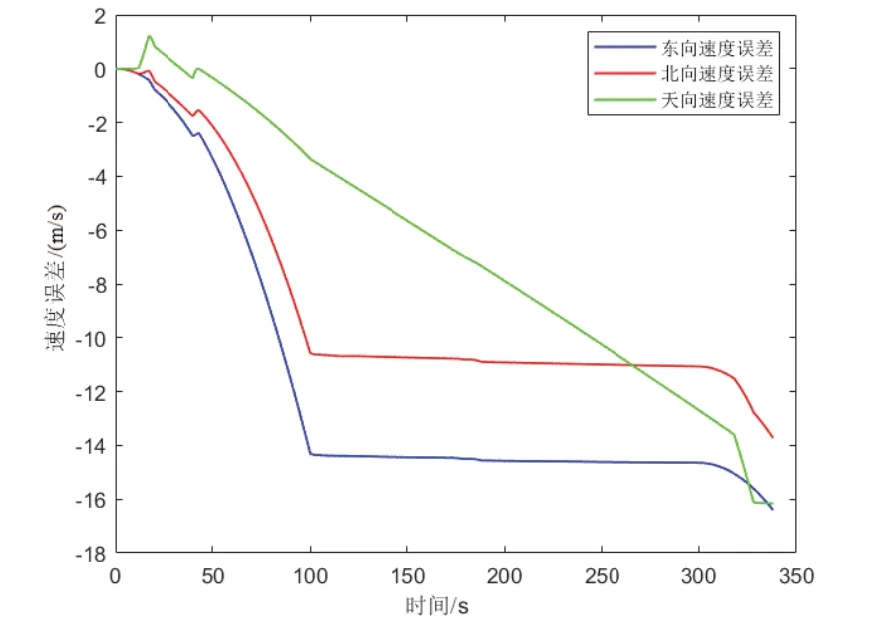
图7 速度误差Fig.7 Velocity error

在初始飞行的125s，只有惯导工作，姿态误差迅速发散，导致速度误差也迅速发散。俯仰角、横滚角、航向角误差分别达到了1.7°、1.4°、1.76°，速度误差分别累积到了14.7 m/s、11.2m/s、1.48m/s。125s后载体变为匀速飞行，图示的姿态误差迅速收敛并保持稳定，表明本方法成功捕捉到非机动工况窗口，滤波器的工作条件被触发并开始工作，在175s时，俯仰角误差为0.036′，横滚角误差2.46′，航向角误差1.08′。东向、北向速度误差也得到快速、有效的抑制。

在175s到187s之间载体做连续机动飞行，机动导致加速度计输出远大于重力加速度，滤波器停止工作，姿态误差又开始发散。187s后，飞行器继续做匀速运动，滤波器得以重启，姿态误差重新收敛。300s后人为关闭滤波器工作，捷联惯导姿态误差重新发散。

观察图7中125～300s时间段几乎平直的东向和北向速度误差，发散抑制程度显著，正是由于滤波提升了数学平台精度。由于捷联惯导高度通道发散，天向速度误差自身无法抑制，需借助其它方式补偿。

此外，本方法还能有效估计出载体系下的陀螺漂移，如图8所示。

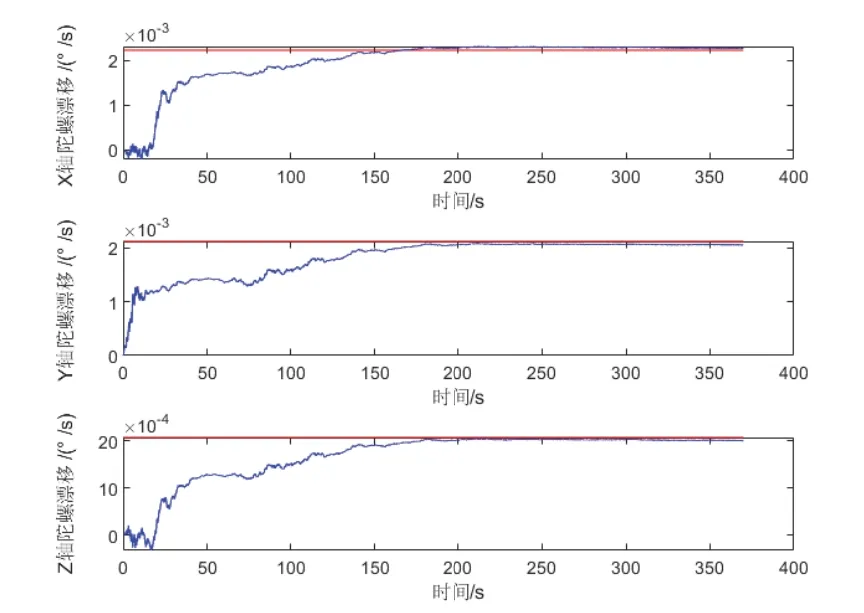
图8 陀螺漂移估计值Fig.8 Estimated value of gyro drift

为验证加速度计噪声对姿态精度的影响，分别选取加速度计随机噪声标准差为5mg、20mg、40mg、80 mg作为仿真条件开展仿真，同时，拣选文献[12]中互补滤波这一现有典型方法进行复现，对于姿态结果做比较。针对飞行过程中的非机动工况时段，本方法的姿态角标准差列于表1。文献[12]中的互补滤波方法计算的姿态角标准差列于表2。

表1 不同加速度计噪声下本文方法姿态标准差Tab.1 Attitude error Std of thismethodunder different accelerometer noise

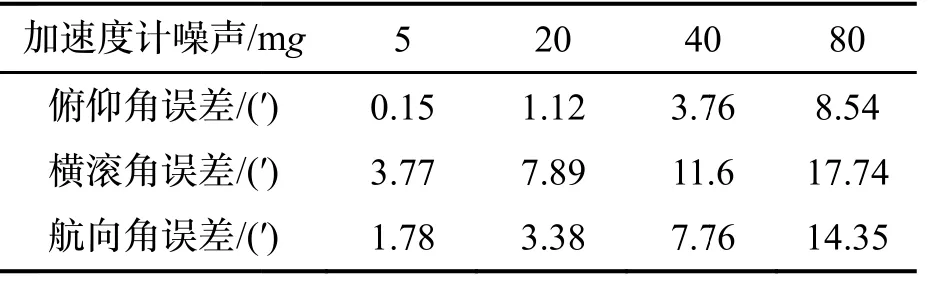
表2 不同加速度计噪声下的互补滤波算法的姿态标准差Tab.2 Attitude error stdof thecomplementary filtering methodunder differentaccelerometer noise

对比表1、表2，随着加速度计噪声水平的增加，本文所提方法对于组合系统姿态精度降低效果显著，当随机噪声强度增加至80 mg时，本文方法姿态精度优于8′，与现有互补滤波[12]相比优势明显，姿态精度提高约50%。此外，本文方法算法中还具有观测噪声方差R1随着加速度计输出的自适应调节机制，也有助于提高滤波精度。

4 基于转台的物理试验

为验证算法实用性，利用ADIS16488九轴MEMS惯组进行转台试验并分析结果，IMU噪声特性见表3。

表3 IMU噪声特性Tab.3 IMU noise specifications

试验现场装置如图9。

图9 MEMS惯组和转台试验装置Fig.9 MEMS IMU and the turntable device

4.1 静态试验

将IMU 紧固在转台内框台面，调整其本体三轴与转台XYZ三轴重合。静态采集数据150s 静态并分析，观察对比有无本文滤波方法的性能差异。

4.2 动态试验

控制转台以70°/s的角速率绕Z轴(天向)在0～110°范围内做往复运动，采集60s数据。在0°和110°时会因角速度方向变化有电机启、停，是一种机动状态，可验证本文算法的非机动窗口捕捉性能。

4.3 结果分析

试验结果如图10～12。由图10～11可知，静态条件下，不做漂移补偿任由陀螺积分计算的姿态角在150s时刻分别产生了高达21.15°、25.52°、63.77°的漂移误差。在基于转台的机动动态测试中，陀螺积分方法在60s过程中分别产生了最大值为4.953°、4.375°、51.28°的三轴最大姿态角误差，图11中已用O标出。

图10 有无本文滤波算法的静态数据三轴姿态角误差对比Fig.10 Attitude angle error comparison of the static sampling data with vs.without the algorithm of this paper

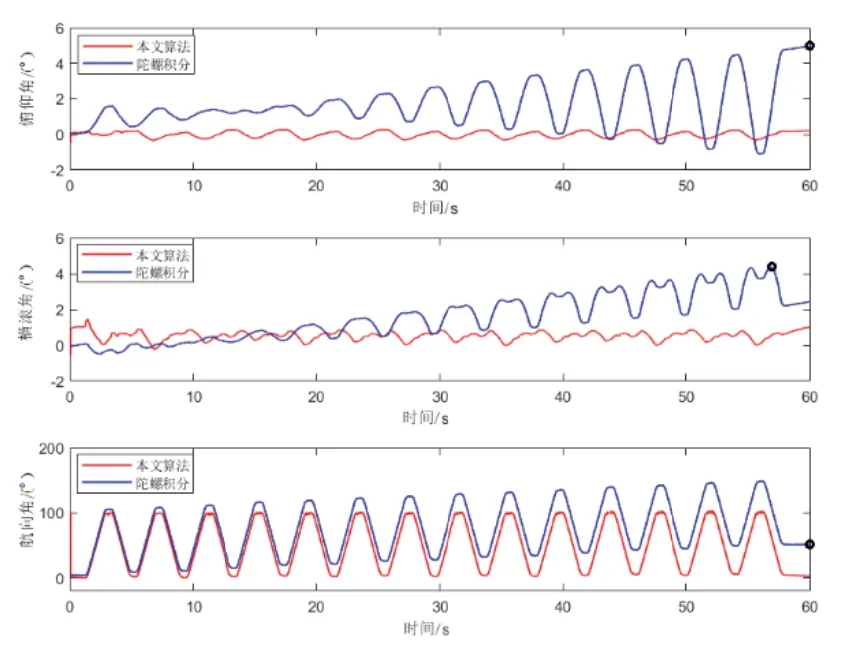
图11 转台动态运动下两种方法姿态角对比Fig.11 Attitude comparison with vs.without the algorithm of this paper under turntable maneuvering motion

试验结果表明，本文方法在静、动态测试中均能有效修正姿态误差。然后，复现现有典型的互补滤波算法[12]得到的测试结果如图12所示。

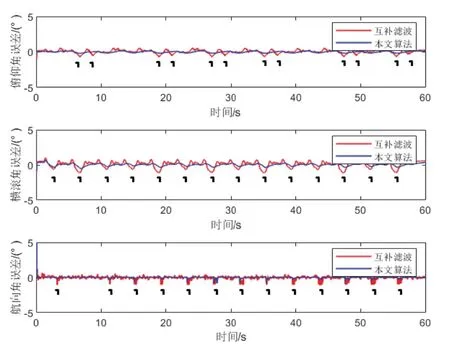
图12 动态条件下本算法与典型的互补滤波方法误差对比Fig.12 Attitude error comparison between the typical complementary filtering method and the method of this paper under turntable dynamic motion

本方法与现有的互补滤波[12]算法相比，考虑了加速度计噪声以及载体机动对姿态误差的影响，并根据加速度计输出值将载体分为三种机动情形，并自适应调整式(22)中的R1。分析图12，在动态测试中，转台启、停产生的机动会影响加速度计输出值，进而产生姿态修正误差，本文所提方法在计算过程中能够识别出此机动，并将其判定为低加速度机动过程，进一步减小机动带来的姿态误差，图中□标志为本方法判定出的机动时刻。而现有互补滤波方法明显受此机动影响，在过程中产生较大姿态误差，抗机动性能不如本文方法。

5 结 论

针对低成本中低精度惯性自主导航，全航段或航时中非机动窗口的占比往往都很大。根据非机动窗口下的加速度计比力等于重力的现象，构建了基于加速度计、磁强计的新型滤波方法。建立了加速度计比力值判定指标确定飞行中的非机动窗口，通过重力矢量先行修正水平姿态角，然后利用已修正的水平姿态角以及磁强计输出值再行修正航向角，滤波效果显著提升。给出了计算机仿真结果，在陀螺漂移6 °/h，磁力计精度100 nT器件参数仿真条件下，姿态精度优于3 ′，速度误差发散程度也得到抑制，同时进行了加速度计精度对该方法有效性的仿真，加速度计随机噪声强度为80 mg时，该方法姿态精度优于8 ′，与现有的互补滤波[13]方法相比姿态精度提高50%。利用MEMS惯组ADIS16488开展了转台试验，试验数据处理结果表明，该方法运行正确，可有效修正姿态误差，比现有互补滤波[12]方法更具抗机动性。该方法完全自主，精度较高，可有效提升中等精度惯性器件的导航性能，具有工程应用价值。