一种基于自适应遗传算法优化BP神经网络的漏磁缺陷量化框架

刘思娇，郑 莉，焦晓亮，呼 婧

(北京华航无线电测量研究所，北京 100013)

随着石油和天然气市场的飞速发展，油气管道的安全问题越来越受到重视，管道缺陷的量化对于预防管道事故的发生起着十分重要的作用。BP神经网络方法已被应用到漏磁缺陷量化领域[1-2]，韩文花等[3-4]提出了用遗传算法对缺陷进行反演，但是传统遗传算法优化BP神经网络应用于大量缺陷反演的计算存在训练速度慢、量化精度低等缺点[5-6]。笔者将自适应遗传算法优化的BP神经网络应用到管道漏磁缺陷量化中，即根据管道漏磁实测缺陷的特点，自适应遗传算法自主调节变异率和交叉率，进而提高计算速度，降低量化误差[7]。

1 算法的基本原理

1.1 误差逆传播算法

误差逆传播算法(BP神经网络算法)是神经网络算法的一种，网络由信号的正传播和误差的逆反馈组成。正传播，即将训练样本输入网络，逐层向前传播；误差逆反馈，即计算输出层的误差，逆向反馈给隐层单元，再将误差方向传播回去，用连接全输入端的实际信号和输出端的等效误差确定连接权的修正量，来更新各层间连接的权重和阈值[8]。在算法训练过程中，这两个阶段循环进行，直至满足停止条件。

1.2 遗传算法

遗传算法是用于解决搜索和优化问题的启发式学习方法,其结合了遗传学中基于适应度逐代选择的存活原理，用选择算子、交叉算子、变异算子去产生可延续的后代，进而找到最匹配的解决方案。

遗传算法也是通过循环遍历的方式进行最优筛选的，例如，在第t代种群为P(t)，经过遗传算子运算胡，得到第t+1代群体，遗传算法流程如图1所示。

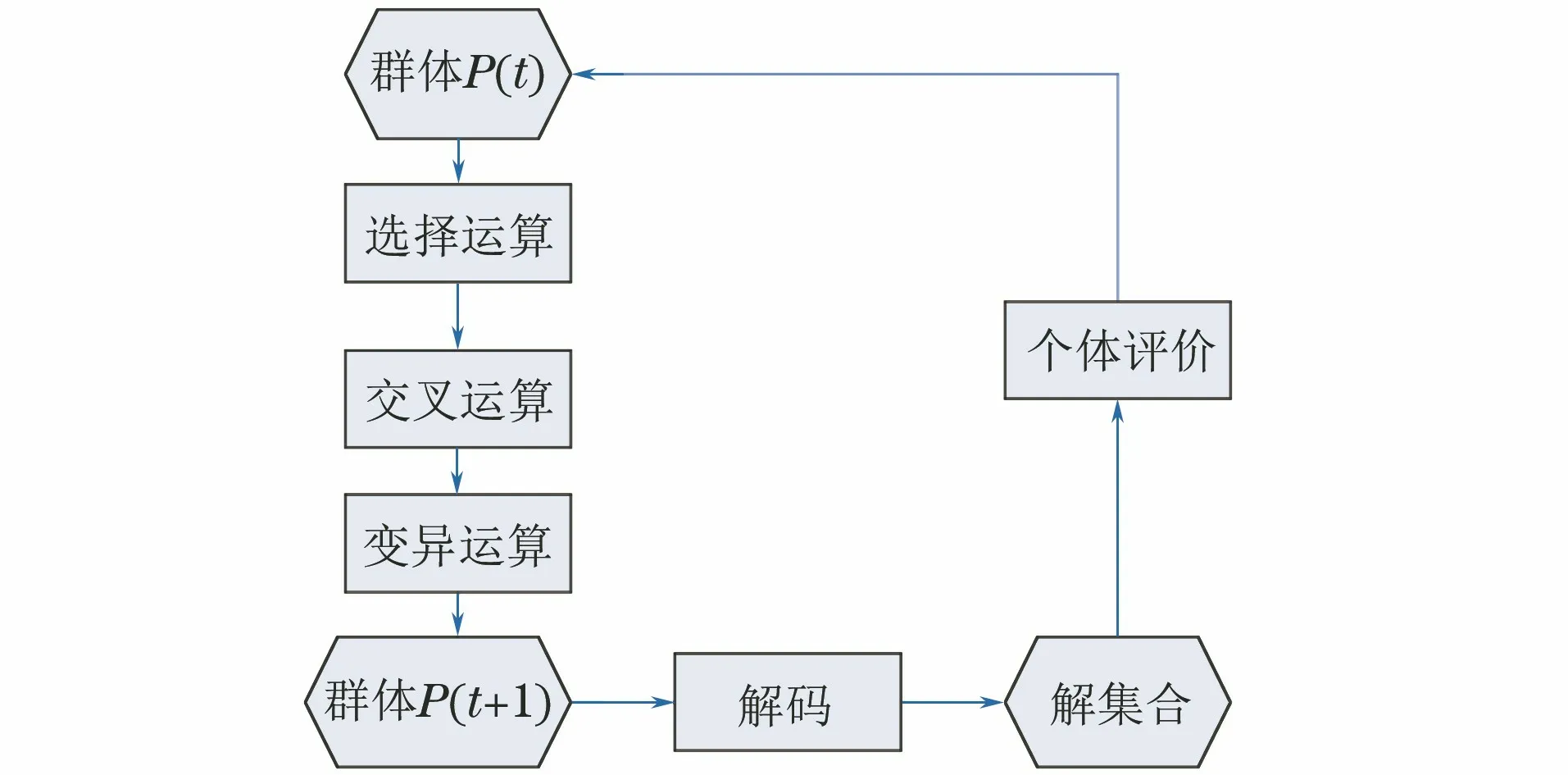
图1 遗传算法流程

1.3 算法存在的缺陷

简单的遗传算法忽略了逐代运算时种群个体的优劣性，只利用了人为设定的交叉率和变异率进行寻优运算，算法泛化能力低，在进行神经网络优化时增加了网络优化难度，缺陷尺寸量化精度不高。

2 自适应遗传算法

2.1 自适应遗传算法原理

自适应遗传算法利用适应度在种群中的顺序排列和种群的进化状态，自动调节遗传算子的交叉率和变异率，使算法泛化能力增强。

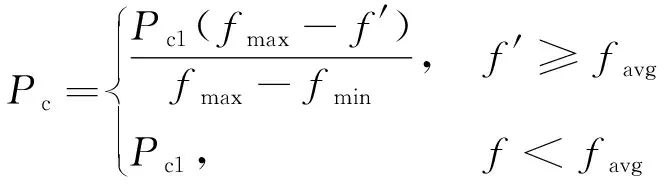
(1)

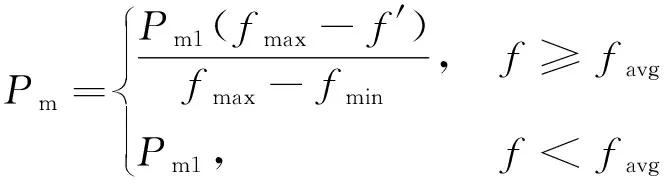
(2)

式中：f′为初代个体的适应度最大值；f为次代个体的适应度值；fmax，fmin分别为个体适应度的最大值，最小值;favg为整个种群适应度的平均值；Pm1为初代变异率；Pc1为初代交叉率。

由式(1),(2)可知，个体适应度值趋于最大值时，其交叉率和变异率均趋近于零，说明在后期种群进化寻优的过程中，自适应遗传算法可以对优秀的子代个体进行保留，增加交叉和变异操作的泛化能力，进而提高简单的遗传算法对于误差逆反馈网络对于初始权值的选择。

2.2 自适应遗传算法优化误差逆反馈神经网络框架

将遗传算法应用到误差逆反馈中，主要是用遗传算法优化误差逆反馈神经网络的初始权值，误差逆反馈神经网络运用优化后的初始权值进行网络训练，对训练数据更具有适用性。自适应遗传算法优化BP神经网络流程如图2所示。

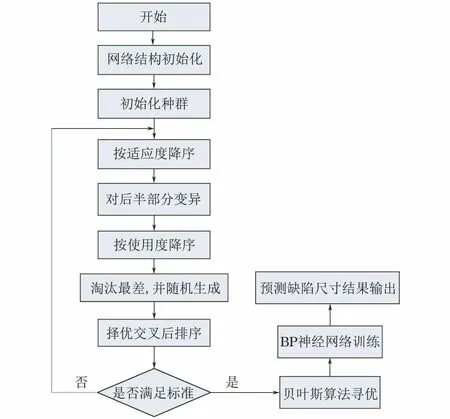
图2 自适应遗传算法优化BP神经网络流程

2.2.1 选择算子

采用轮盘赌法的选择策略，使种群中优秀的个体以较大概率遗传到下一代，增加优秀个体的适应度。

2.2.2 交叉算子

选择算子完成后，种群中个体两两组合成为交叉算子的初代个体，由两个初代种群的适应度计算出自适应交叉率，进行交叉运算。

2.2.3 变异算子

基于漏磁缺陷尺寸的多样性及连续性,采用多点变异的方式，相较于传统的单点变异，更适用于个体染色体长度较大的情况。在代数逐渐增加的进化过程中，产生变异的基因位的个数会逐渐减小，对变异点进行如下定义。

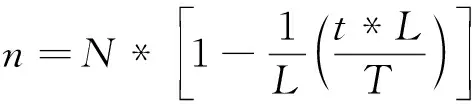
(3)

式中:N为染色体基因长度；t为种群当前进化代数；T为种群进化目标代数；L为大于1的自然数；中括号表示向下取整。

2.2.4 适应度函数

适应度函数是评价算法选择何种路径进化的重要判别标准，即对收敛速度及最优后代的产生有决定性影响。设置适应度函数为

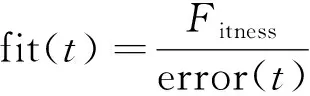
(4)

式中:error(t)为其对应的误差逆反馈网络输出的误差标准差，适应度随着error(t)的减小而增加；Fitness为常数。

2.2.5 误差逆反馈网络的框架搭建

采取自适应遗传算法优化误差逆反馈神经网络，基于数据特点自适应定义变异率和交叉率，为误差逆反馈网络选取适应度最高的初始权值，同时定义如下网络框架，具体描述如下所述[9]。

(1) 首先将数据进行归一化，构建网络输入层传输函数采用log-sigmoid，输入值和输出值在0和1之间；输出层传递函数采用线性输出函数purelin，输入和输出值可取任意值；训练函数采用贝叶斯正则法进行训练。

(2) 设置种群的规模为50，随机生成50组个体长度为57的神经网络连接值，其中每个连接值的变化范围为[-1，1]，然后对每一组连接值进行初始化。

(3) 进行遗传算法运算，迭代过程中不断调整交叉率和变异率，依据上一节选择、交叉、变异方法进行优胜劣汰的遗传策略。

3 结果分析

3.1 样本

缺陷数据库包含天津直管牵拉和水压环路试验采集数据的缺陷库，共1 567个缺陷样本。所有缺陷样本均从轴向去噪之后的数据中提取，训练集与测试集比例为4…1。

缺陷长度分别为10，20，40，60 mm，宽度分别为10，20，40，60 mm，深度分别为1，3，5，7 mm。其中内缺陷为895个，外缺陷为672个。

3.2 量化结果分析

3.2.1 训练速度

对比传统遗传算法和自适应遗传算法对神经网络训练速度的影响，可以看出，传统遗传算法需迭代的次数多，且得到的误差远大于目标误差；而自适应遗传算法迭代次数少，训练速度快，量化精度也较传统遗传算法有很大提高。传统遗传算法优化BP神经网络训练集迭代次数如图3所示，自适应遗传算法优化BP神经网络训练集迭代次数如图4所示。

图3 传统遗传算法优化BP神经网络训练集迭代次数

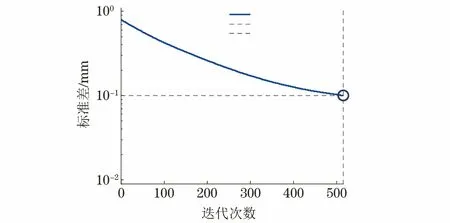
图4 自适应遗传算法优化BP神经网络训练集迭代次数

3.2.2 量化误差

比较传统遗传算法和自适应遗传算法优化BP神经网络对于缺陷长宽深量化结果在不同评价指标的误差，结果表明：自适应遗传算法优化BP神经网络算法在训练集和测试集的评价指标满足率较传统遗传算法优化BP神经网络有明显提高，说明自适应遗传算法优化BP神经网络有更好的学习能力；同时，自适应遗传算法优化BP神经网络对比传统遗传算法计算速率更快，迭代次数少，计算效率更高。 传统遗传算法和自适应遗传算法优化BP神经网络的长度、宽度和深度量化结果如表1～6所示(表中A为管道壁厚，9.5 mm)。

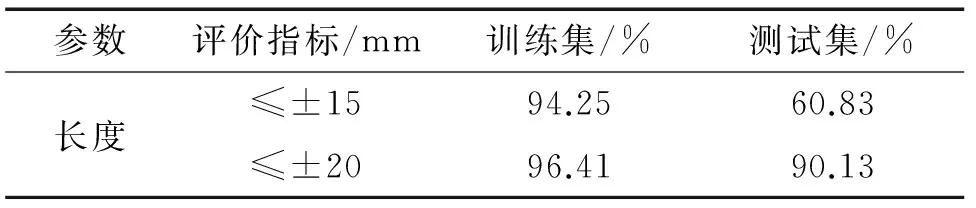
表1 传统遗传算法优化BP神经网络长度量化结果

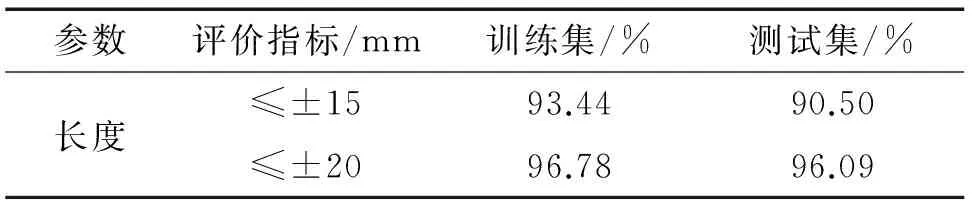
表2 自适应遗传算法优化BP神经网络长度量化结果

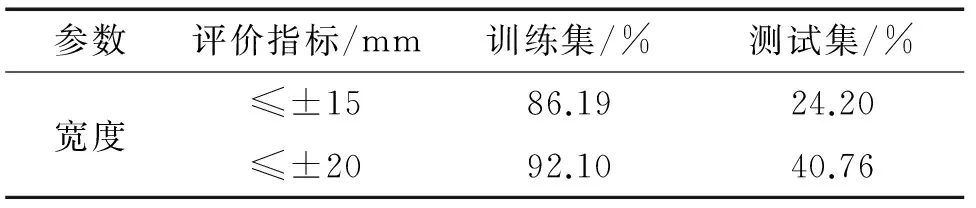
表3 传统遗传算法优化BP神经网络宽度量化结果

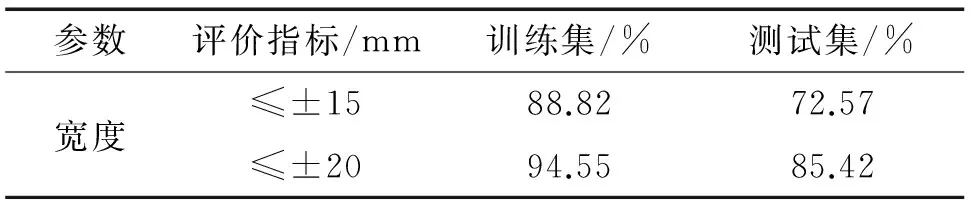
表4 自适应遗传算法优化BP神经网络宽度量化结果

表5 传统遗传算法优化BP神经网络深度量化结果

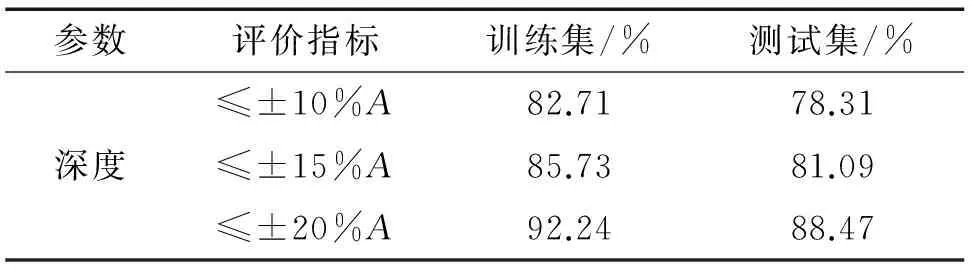
表6 自适应遗传算法优化BP神经网络深度量化结果

4 结语

在管道漏磁缺陷量化的计算过程中，针对传统遗传算法的缺点，采用自适应遗传算法，根据实测管道缺陷的特点进行交叉率和变异率的调节和选取，相较于固定的交叉率和变异率，此方法提高了遗传算法的计算速度,降低了实测数据的计算误差。