我国人口出生率的分析与预测

孙鑫鑫 高 燕 袁 汐 王增相

( 1)山东师范大学数学与统计学院，250358，济南； 2)阿萨巴斯卡大学商学院，T9S3A3，艾伯塔，加拿大 )

1 引 言

我国是一个人口大国，人口问题一直是关乎国计民生的热门话题.根据人口出生率的统计数据，可以发现全国人口出生率近年来总体呈现下降的趋势，尤其是近十年来的人口出生率一直维持在12‰左右，如果人口出生率一直保持在较低的水平势必会给社会带来许多问题.2016年二胎政策全面放开，文献[1]曾提出全面实施二胎政策可能会缓解人口出生率下降的趋势.事实上2016年和2017年这两年的全国人口出生率较之前确实有所上升，分别达到了12.95‰和12.43‰，但这可能只是短期效应，未来会怎样发展还需通过严谨科学的研究进行预测，只有这样才能更客观清晰地了解未来我国人口出生率的趋势.

本文对我国从1949年到2017年的人口出生率进行分析，建立时间序列模型预测未来5年我国的人口出生率是继续呈下降趋势还是会达到一个平稳的状态.由于影响出生率的因素非常多，因此在建模过程中可能会出现很多诸如平稳性检验、白噪声检验不通过或者模型拟合情况不好等问题，本文旨在解决这些问题，最终使残差变成白噪声序列，并且建立一个合理的模型对未来五年我国的人口出生率进行预测.

2 数据来源及分析

2.1数据来源从《中国统计年鉴》中选取自1949至2017年全国的人口出生率作为原始数据，并选择最合适的预测方法预测未来5年的全国人口出生率(表1).

2.2数据特征分析将1949-2017年的全国人口出生率绘制成折线图,如图1所示.

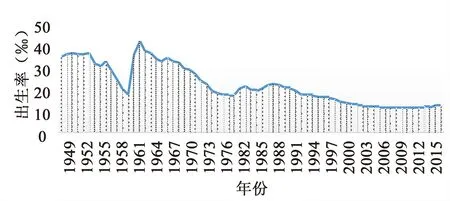
图1 全国人口出生率折线图

表1 1949-2017全国人口出生率统计

从图1可以看出，我国的人口出生率大致可以分为五个阶段：早期的高出生率阶段，20世纪70年代出生率大幅下降阶段，20世纪80年代出生率有所反弹阶段，20世纪90年代出生率持续下降阶段和近年来低出生率阶段.根据国家统计局人口普查数据，可以得到如下结论.

1) 1949-1970年的高出生率阶段.这个阶段的人口出生率平均值在30‰左右，新中国成立后，社会安定，经济发展，人们的生活水平和医疗条件都不断改善，因此在这个阶段总体上保持着高出生率.2) 1971-1979年出生率大幅度下降阶段.这个阶段人口出生率大幅度下降至17.82‰ ，这是因为人口高速增长带来了巨大的压力，人们认识到控制人口已迫在眉睫，在全国发出了实行计划生育的号召，并制定和完善了计划生育政策，导致这个阶段出生率呈现出大幅下降趋势.3) 1980-1987年出生率小幅度的反弹阶段.这个阶段人口出生率回升至23.33‰，这是因为在20世纪60年代初“第二次人口生育高峰”中出生的人口陆续进入生育年龄，使得人口出生率出现回升.4) 1988-2004年持续的下降阶段.这个阶段人口出生率下降到了12.29‰，主要是受到了计划生育政策不断加强和完善的影响.5) 2005-2018年人口低出生率阶段.这个阶段的人口出生率平均值在12.10‰左右，这个阶段仍然受计划生育政策的影响，加之养育孩子的成本增大，女性的生育观念发生转变等因素，使得出生率保持在较低水平.

3 人口出生率的时间序列模型

3.1时间序列分析基本步骤时间序列分析是常用的定量预测方法之一.应用时间序列分析建模可以寻找出序列值之间相关关系的统计规律，并拟合出适当的数学模型来描述这种规律，进而利用这个拟合模型预测序列未来的走势.

建立时间序列分析模型首先要对数据进行平稳性检验以及纯随机性检验，然后计算样本自相关系数和偏自相关系数.依据计算出来的自相关系数和偏自相关系数，按照ARMA模型定阶的基本原则对模型进行定阶.时间序列分析的基本模型如下[2-4]：

1) 自回归模型(AR模型).一般的p阶自回归模型记为AR(p)，它有如下结构：

(1)

该模型的基本假设如下：

H1模型最高阶数为p阶；

H2随机干扰项序列{εt}为零均值白噪声序列；

H3现在的随机干扰与过去的序列值不相关.

2) 移动平均模型(MA模型).一般的q阶移动平均模型记为MA(q)，它有如下结构：

(2)

该模型的基本假设如下：

H4模型最高阶数为q阶.

H5随机干扰项序列{εt}为零均值白噪声序列.

3) 自回归移动平均模型(ARMA模型).一般的自回归移动平均模型记为ARMA(p,q)，它有如下结构：

(3)

该模型基本假设是AR(p)模型基本假设和MA(q)模型基本假设的结合.

4) 求和自回归移动平均模型(ARIMA模型).一般的求和自回归移动平均模型记为ARIMA(p,d,q)，它有如下结构：

(4)

当d=0时，ARIMA(p,d,q)模型实质上就是ARMA(p,q)模型，因此，差分运算结合ARMA模型其实就是ARIMA模型.

3.2数据预处理建立时间序列模型之前，首先要对人口出生率序列进行平稳性和纯随机性检验.

1) 平稳性检验及平稳化处理.首先画出原始数据的时序图，如图2所示.

图2 1949-2017全国人口出生率时序图

由图2可以明显看出原始数据序列为非平稳序列，但是为了保证结果的客观性，还需对全国人口出生率采用Eviews软件进行单位根检验，判断其是否平稳，结果显示单位根统计量ADF=-1.660 242，大于Eviews软件给出的显著性水平(1%～10%)对应的ADF临界值，这就说明该序列是非平稳的.为了可以对序列进行分析，要采取措施使其平稳化.让序列变平稳的方法有两种，分别是对数法和差分法.应用对数法可以绘制出1949年到2017年全国人口出生率自然对数的时序图(图3).

图3显示取对数之后的序列保持了原序列的变化趋势，运用Eviews软件对取对数之后的人口出生率序列进行单位根检验，结果显示单位根统计量ADF=-1.147 253，大于Eviews软件给出的显著性水平(1%～10%)对应的ADF临界值，这说明该序列仍是非平稳的.上述全国人口出生率对数序列含有曲线趋势，通常二阶差分就可以提取出曲线趋势的特征值，因此接下来对原始数据取对数后的序列进行二阶差分，检验其是否平稳(图4).

图4 1949-2017全国人口出生率取对数后二阶差分时序图

由图4可以看出，该序列始终在0点左右随机波动，并且波动的范围有界，因此能够确定原始数据取对数再进行二阶差分之后的序列平稳.但是这样判断数据的平稳性有主观色彩，为了保证客观，在此采用Eviews软件对取对数后二阶差分的数据进行单位根检验，判断其是否平稳.结果显示单位根统计量ADF=-7.921 190，小于Eviews软件给出的显著性水平(1%～10%)对应的ADF临界值，这就说明该序列是平稳的.因此，应该建立ARIMA模型，且差分的阶数d等于2.

2) 纯随机性检验.在将数据平稳化之后，为了确定平稳序列是否值得继续分析，还需要对得到的平稳序列进行纯随机性检验.纯随机性检验也叫白噪声检验，它是用来检验平稳序列是否为纯随机序列的一种方法，若得到的平稳序列为非白噪声序列，则可以进行模型拟合.

纯随机性检验的原假设：延迟期数小于或等于m期的序列值之间相互独立.

纯随机性检验的备择假设：延迟期数小于或等于m期的序列值之间有相关性.

纯随机性检验的检验统计量为

(5)

当p>α时，不能拒绝原假设，需要停止对该序列的统计分析.

P<α时，拒绝原假设，可以继续进行建模.

取置信水平α=0.05，采用SAS软件进行白噪声检验[5，6]，其结果如表2所示.

表2 白噪声的自相关检验

由表2显示的纯随机性检验的结果可以看出，LB统计量的P值小于置信水平α=0.05，因此可以判定取对数再二阶差分后的序列是非白噪声序列，可以利用该序列值进行模型拟合.

3.3模型的识别通过观察平稳序列的自相关结果和偏自相关结果来选择阶数适当的模型进行拟合， 用SAS软件可以得到序列的自相关结果和偏自相关结果(表3、表4).

表3 自相关

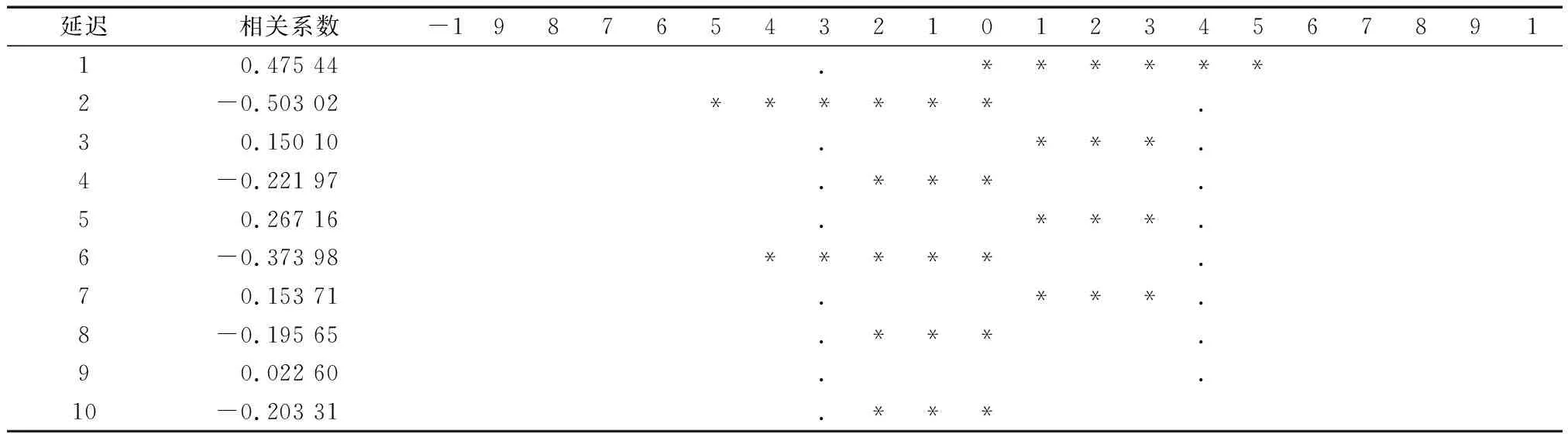
表4 偏自相关

从表3中可以看出，除了延迟0阶和1阶的自相关系数在2倍标准差范围之外，其余阶数的自相关系数都在2倍标准差范围内来回波动.依据自相关系数的这个特点可以判断该序列有短期相关性，从而进一步说明该序列是平稳的.同时，可以认为该序列自相关系数为2阶截尾.表4中偏自相关系数呈现出拖尾的性质.

结合自相关系数和偏自相关系数的性质，初步为拟合模型定阶为MA(2)，建立的模型为ARIMA(0,2,2)，模型公式如下：

(6)

3.4参数估计确定好模型的阶数之后，应该对拟合的模型进行参数估计，本文使用条件最小二乘估计方法对初步拟合的ARIMA(0,2,2)模型进行参数估计(表5).

表5 条件最小二乘估计

由表5可以看出MU不显著，而其他参数都是显著的.接下来要去掉常数项再次估计未知参数，其结果如表6所示，由表6可以看出两个未知参数均显著.

表6 条件最小二乘估计

3.5模型检验模型的显著性检验主要检验模型整体的有效性.一个好的拟合模型可以提取观察值序列中几乎所有与样本相关的信息，也就是说残差序列应该为白噪声序列.因此模型的显著性检验也被称为残差序列的白噪声检验.

模型检验原假设：ρ1=ρ2=…=ρm=0,∀m≥1.

模型检验备择假设：至少存在某个ρk≠0,∀m≥1,k≤m.

模型检验统计量为

(7)

假如拒绝原假设，这说明残差序列中还留有相关信息，拟合的模型ARIMA(0,2,2)不显著，模型的显著性检验不通过；假如不能拒绝原假设，就认为该拟合模型是显著有效的，模型的显著性检验通过.模型的显著性检验结果如表7所示.

表7 残差白噪声检验

从表7可以看出，延迟6阶、12阶、18阶、24阶的LB统计量的P值均大于α=0.05，可知残差序列通过了白噪声检验，也就是说残差序列为白噪声序列.该拟合模型ARIMA(0,2,2)显著成立，可以表示为

2lnxt=(1+1.231 29B+0.250 16B2)εt.

(8)

3.6模型的优化当拟合模型为ARIMA(0,2,2)时，AIC的值为-100.27，对模型重新进行定阶，尝试是否有其他合适的模型AIC的值小于-100.27.经过尝试后，发现当拟合模型为ARIMA(1,2,2)时，AIC的值更小，为-100.793，根据AIC准则，更优的模型为ARIMA(1,2,2).当拟合模型为ARIMA(1,2,2)时，其参数估计的结果如表8所示.由表8中的P值可以看出参数估计均显著，其模型检验结果如表9所示.

表8 优化后条件最小二乘估计

表9 优化后残差白噪声检验

由表9可以看出残差序列为白噪声序列,最终拟合模型ARIMA(1,2,2)显著成立.该模型得到的拟合结果的输出形式可以表示为

(1+0.457 84B)2lnxt=(1+1.692 47B+0.708 18B2)εt.

(9)

4 预测结果

采用建立的ARIMA(1,2,2)模型对未来5年的全国人口出生率进行预测[7-11]，结果如表10所示.

表10 预测结果

图5 拟合与预测图

图5中黑色星号表示全国人口出生率对数序列观察值，红色连续曲线表示拟合序列曲线，绿色曲线表示拟合序列的95%上下置信限.根据图5可以初步判断模型的拟合效果较好，接下来利用2018年的真实数据与预测数据进行比较，进一步验证模型的有效性.

本文以1949-2017年的数据为基础建立时间序列模型，预测出了2018-2022年的全国人口出生率，其中预测的2018年人口出生率对数为2.498 1，它的95%置信区间为(2.279 4,2.716 8)，而2018年人口出生率的真实值为10.94‰，取对数后为2.39，真实值在置信区间范围内，证明模型拟合效果良好，该模型得到的数据可信.

由于建立ARIMA(1,2,2)模型时采用的序列是原始数据取对数之后的数据，因此得到的预测结果也是取对数之后的形式，还需要对得到的结果进行变换，才能最终得到未来五年的全国人口出生率(表11).

表11 未来五年全国人口出生率预测值

5 结论与建议

通过对1949-2017年全国人口出生率的原始数据进行时间序列分析，建立了ARIMA(1，2，2)模型，对未来五年的全国人口出生率进行预测，得到未来五年全国人口出生率分别为12.16‰、12.23‰、12.25‰、12.19‰、12.27‰.从数据可以看出2016年和2017年人口出生率确实是有所提高，但是预测结果显示未来5年仍然保持低人口出生率，这个结果与引言中二胎政策放开使得2016年和2017年出生率短暂提高是一致的.

针对人口出生率维持较低水平这一现状，提出以下建议：

1) 完善二胎政策.全面实施二胎政策的计划刚刚起步，仍存在许多没有考虑到的细节.因此要积极完善二胎政策，既不能造成大众都不响应该政策，又不能导致出生率突然增大影响国家其他方面的发展.

2) 建立健全社会保障制度.比如为老人开办养老保险；为生育二胎的家庭提供补助；加强对公共托幼服务的职业培训和政府监督等.

3) 为女性提供更多就业支持.女性担心生育之后找工作难度加大，因此为女性提供更多就业支持有助于提高人口出生率，就业环境越宽松，女性才能越放心地去生育.

4) 人口政策应该致力于改变趋势性的斜率.本文所建立的二阶差分模型表示人口出生率带有与时间相关联的趋势性，二阶差分之后所获得的时间序列实际上描述了出生率趋势之斜率随时间的变动情况.具体来说，如果希望人口增长提速 (如用来弥补劳动力短缺)，应该维持趋势性的斜率为正来促使人口加速增长.