单载波GMSK信号的高精度频偏估计算法

高 静，桑 田，罗 韬

单载波GMSK信号的高精度频偏估计算法

高 静1, 2，桑 田1, 2，罗 韬3

(1. 天津大学微电子学院，天津 300072；2. 天津市成像与感知微电子技术重点实验室，天津 300072；3. 天津大学智能与计算学部，天津 300350)

在接收机中，频偏估计的精度决定了信号解调的准确性。GMSK调制作为深空通信的调制方式之一，复杂的空间环境对高精度频偏估计的实现带来了大的挑战．为了进一步提高GMSK信号频偏估计的精度，本文提出了一种基于快速傅里叶变换(FFT)的高精度插值估计算法．该算法是一种非数据辅助类算法，不需要依赖导频序列，可以与数据辅助类算法结合使用．在GMSK信号的传输过程中，复杂的大气环境导致传输信道具有很低的信噪比。在低信噪比的信道环境中，估计算法要达到理想的精度，需要提高其抗噪声干扰能力．在本文中，高精度插值估计算法首先对接收信号进行FFT运算，得到接收信号的频谱信息，实现对信号频率的初步估计．之后将得到的FFT最大幅值谱线与其相邻谱线中心点的谱线值进行比较，将具有最大幅值的点作为峰值谱线．最后，对峰值谱线进行数学计算，得到估计的频偏值．本文提出的频偏估计算法可以提高抗干扰能力，降低噪声对有用信号的影响并减少误判情况，提高估计精度．利用计算机模拟该频偏估计算法的估计性能，仿真结果表明：所提出算法的频率估计精度优于其他现有算法，具有更加平稳的估计效果，降低了算法工作的信噪比门限，可用于各种环境下GMSK信号的载波频偏估计．

频偏估计；快速傅里叶变换；低信噪比门限；高精度

GMSK调制方式因其恒包络、频谱利用率高的特点被国际空间数据系统咨询委员会列为深空通信的调制方式之一[1]．GMSK信号的解调方式分为非相干解调与相干解调．在特定领域如空间通信方面，由于非相干解调门限的限制，只能采用相干解调．同时，由于空间通信中传输通道中的大气环境复杂，信噪比(signal-to-noise ratio，SNR)很低，一般处于0～20dB[2]．所有这些问题给信号的检测和解调带来了巨大的挑战．频率偏移估计的准确性对GMSK信号的解调具有重要意义[3-4]．

GMSK信号的同步方法可以按照是否依靠导频序列分为数据辅助(data-aided，DA)类和非数据辅助(non-data-aided，NDA)类[5]．DA方法通过在导频插入特定的序列进行识别同步．NDA是基于接收信号的非线性获取参数，可以结合DA方法进一步提高精度．在NDA方法中，田鹏武等[6]基于MSK的循环谱提出一种频率估计方法，但估计范围受到采样率的限制．Magana等[7]提出一种基于ad hoc的GMSK信号载波频率估计方法，但是它具有很高的复杂度．按照分析信号的不同，也可将频率估计方法分为时域类和频域类．时域类方法中，Kay算法[8]的原理简单易于实现，但工作门限高不适用于低SNR环境．Fitz算法[9]具有较好的低信噪比性能，但是估计范围有限，且范围的扩大会导致运算量快速增加．频域类方法大多基于最大似然估计[10]，是利用FFT得到信号的谱线，利用频偏值与谱线的关系求解．

FFT法的优点是具有较快的速度，适用于实时性系统[11]．但是，FFT的栅栏效应限制了频率估计的范围，且低信噪比环境下精度不高．为实现更精确的频率估计，国内外的学者们基于FFT提出了很多改进算法．Rife算法[12]具有实现简单、计算量小的优点，但估计精度随频偏值的变化产生大的波动．为此，Quinn[13]利用谱线的最大值与次大值之比取实部改善了波动情况，但量化频率点附近的估计效果依然较差．邓振淼等[14]进一步提出了M-Rife算法，通过频移使估计频率都位于中心区域，改善了量化频率点附近的估计效果的估计效果，但频移增加了大量计算量．Candan[15]提出了利用3条谱线的估计方法，但是结果仍然有大的误差．Meng等[3]构建辅助方程去除GMSK中的相位信息，在利用频谱信息得到频偏因子后进行插值得到精估计，但估计范围有限．

本文中，利用提出的高精度插值算法进行频偏估计，将点FFT得到的最大谱线与其相邻谱线之间细化，利用细化后的中心点幅值与原峰值点比较得出的最大幅值点作为中心点，减少误判情况，提升估计精度．本文的其余内容划分如下：第1节介绍接收信号模型与直接使用FFT估计存在的问题；第2节阐述单载波频偏算法的思路、原理和实现步骤；第3节仿真分析提出算法的估计性能，并与现有算法进行了对比分析，最后进行总结．

1 信号模型

在接收机中，如图1所示，采用开环算法的数字解调块由数字混频器、捕获、位同步、载波同步、解调、译码几个部分组成．载波同步通过频偏估计后进行频偏补偿来实现，载波同步后的信号进行后续的解调以及译码恢复．

图1 数字解调框图

经GMSK调制后的信号可以表示为

其中

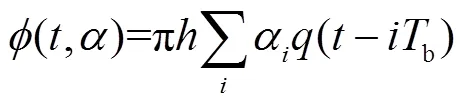
式中：(，)为承载信号的相位信息；为具有等概率值为1的二进制信息序列；为调制指数，在GMSK调制中取0.5；b为符号周期；()是脉冲调制器，它可以表示为

()信号受限于区间[0，b]中，即

式中：为高斯滤波器中连续符号的长度；为带宽，其值为3dB．()定义为

假设()通过AWGN信道传输和并且完成定时恢复．依次通过混频器和带通滤波器后，接收到的信号可以表示为

式中：c为载波频率；d为频偏频率；是调制信号的相位信息(，)；()是加性复数高斯白噪声，服从均值为0、方差为2的高斯分布．

GMSK信号是由频率分量组成的正弦波．基于此，可以利用估计正弦波的载波频率的方法来得到频率偏移量．为防止相位信息对频率估计的干扰，可通过将可用数据重新调制后的两路正交信号和()的两路正交信号分别相乘将去除[3]，得到

式中()是可用数据重新调制后的信号与()相乘后的结果．

对信号()进行周期为s的采样，得到长度为的序列()，即

式中：采样周期s是符号速率b的倍；是有效数据长度．

对()做点FFT变换得到

对得到的频谱进行最大值搜索，最大幅值处的谱线记为1．根据最大似然估计原理，可以得到频偏值与1的关系为

当FFT的点数为时，1的取值范围为0～-1，可以得到此时的估计范围为-1/(2s)～1/(2s)．同时，式(10)表明，算法的估计精度直接与FFT的长度直接相关．长度为的FFT，其最小量化频率为1/(s)．1是最小量化频率的整数倍．实际上，还存在一个小数部分．如图2所示，若为实际上的谱线值，则＝1．

图2 基于FFT的频率估计偏差

当接近0时，此时1两侧相邻谱线的幅值非常接近，当有噪声干扰时，很容易发生误判．若此时判断错误选取右侧谱线为次大值谱线，可知FFT的最大估计误差为

因此，在采用比较相邻谱线大小来获取修正方向的算法中，由于幅值大小相近以及噪声的干扰，很容易发生修正方向的误判，造成大的误差．

2 频偏估计

在基于FFT进行粗估计的方法基础上，进行进一步的精估计以得到更准确的频偏值．为了增强算法的抗噪声能力，以及避免接近0时出现误判的现象，使用具有更大幅值的量化频率中心点进行估计.首先基于FFT进行粗估，由式(8)、(9)可以得到

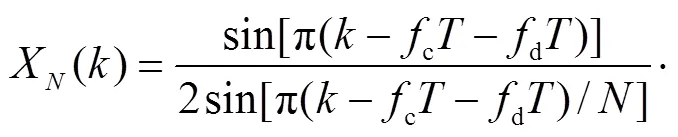
根据||＜0.5，可以得出

由极限定理可知趋于0时，sin近似等于．2值相对于频偏因子来说很大，结合三角函数的性质将式(15)进行化简可以得到

通过整数因子和小数因子可知得到频偏值为

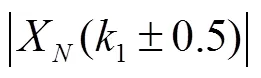
(1)对()进行点采样得到序列()；

(2)对()进行点FFT变换；

(3)利用实信号频谱的对称性，只需搜索频谱的前/2点，找到最大谱线位置1及1+1、1-1，得到对应的频谱幅值；

(6)将3点中最大点处作为中心点，根据最大值得到m的取值；

图3 算法流程

3 算法性能分析

在接收端解调过程中，解调的准确度直接受到频偏估计部分精度的影响．本设计通过计算机模拟对算法进行了仿真与估计精度的评估．在仿真中，传输信道设置为AWGN信道，将有效数据的长度分别设置为8、32和128．GMSK调制中高斯滤波器的时延带宽积b为0.5，采样频率s＝1/s为2.4MHz，载波频率为300kHz．信道中的高斯白噪声服从于(0，2)的高斯分布，信噪比定义为SNR＝10lg(2/22)，s/0＝2/22，其中是有用信号的幅值，SNR位于[-10，10]dB的区间内．在[-0.5，0.5]的区间内取5000个随机值，即仿真次数＝5000．利用均方误差(mean square error，MSE)衡量算法的估计效果，即

最大似然估计方差理论上的下界是克拉美罗界(Cramer-Rao bound，CRB)，即

对Rife算法[12]、Candan算法[15]、最大似然估计(maximum likelihood estimation，MLE)[16]算法、Meng算法[3]和本文提出的插值估计算法进行仿真与分析．其中，由于Meng算法需要利用最大谱线的前后(为正整数)条谱线值进行迭代插值，但文中未叙述插值点数超出谱线范围的情况如何处理．因此在仿真分析中，对于＝3且接近0或0.5时，出现最大谱线的相邻谱线不足3个的情况，只进行基于最大似然估计原理的粗估计．图4(a)、(b)、(c)分别给出了＝8、32、128时各算法在不同信噪比下频率估计的均方误差以及和CRB的比较．可以看出，随着SNR的增加，各算法都逐渐趋近于CRB．所提出的算法提高了量化频率，并且得到的谱线具有更大的幅值，MSE曲线下落更快，在低SNR下具有更好的估计精度，且最终能达到更高的精度，优于其他算法．对图4(a)、(b)、(c)进行比较可以看出，随着的增加，各算法的MSE整体下移，达到稳定估计需要的SNR条件也逐渐降低，在＝8或32时，提出的算法具有低于其他算法2dB的SNR门限，＝128时降低了1dB的SNR门限．

在传统的估计方法中，较小的情况下可能发生修正方向的误判，造成大的误差．为研究频偏值对不同判别方法估计精度的影响，利用MSE评估在不同频偏值下各算法的估计精度．图5(a)、(b)、(c)分别给出了各算法在SNR＝-5dB、0dB和5dB时MSE与的关系．结果表明，MLE算法的MSE随的增大逐渐升高，这是因为MLE算法只能进行量化频率整数倍的估计，而无法对小数倍的进行估计．Rife算法的MSE性能在较小时剧烈波动，原因是在很小时，容易出现方向的误判，Candan算法具有较平稳的估计效果，但在接近0.5时，有一定的升高．Meng算法的缺点与Rife算法相似，容易受到噪声的影响发生修正方向误判的情况．同时，由于在本文中对Meng算法处理的部分信号只采用了最大似然估计，导致在接近0.5时，MSE恶化严重．因此，Meng算法适用的频率范围有限．提出的高精度插值估计算法有利于减少频偏处于量化频率中心时出现错判的情况，具有非常平稳的估计效果．

图4 各算法在不同M值下的MSE随SNR变化情况

图5 不同SNR下各算法的MSE随δ变化情况

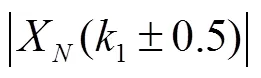
表1 不同算法的插值公式与计算量比较

Tab.1 Comparison of the interpolation formulas of dif-ferent algorithms with the calculated quantities

4 结 语

针对提高GMSK信号相干解调的载波同步精度与降低算法的SNR门限问题，提出高精度插值估计算法．在利用FFT实现粗估计的基础上，计算量化频率中心点的值得到大幅度的谱线，提高了抗噪声能力，降低了算法工作的SNR门限．通过2次搜索更新最大谱线，防止待估频率在量化频率点附近时出现误判情况，提高了估计精度．提出的算法具有低的信噪比门限和平稳的估计效果，适用于各种环境下GMSK信号的解调电路．

［1］ Zhu Hai，Xu Hengzhou，Zhang Bo，et al. Design of efficient LDPC coded non-recursive CPE-based GMSK system for space communications[J]. IEEE Access，2019，7：70654-70661.

［2］ Burzigotti P，Ginesi A，Colavolpe G. Advanced receiver design for satellite-based AIS signal detection[C] //2010 5th Advanced Satellite Multimedia Systems Conference and the 11th Signal Processing for Space Communications Workshop. Cagliari，Italy，2010：1-8.

［3］ Meng Xin，Liu Chen，Teng Jianfu，et al. Frequency offset estimation of satellite-based AIS signals based on interpolated FFT[J]. Wireless Personal Communica-tions，2018，99(1)：35-45.

［4］ Mohamed A J，Christophe L，Alain T. Nonlinear analysis of GMSK carrier phase recovery loop[C]//2016 International Symposium on Signal，Image，Video and Communications. Tunis，Tunisia，2016：230-235.

［5］ Peng Hua，Li Jing，Ge Lindong. Non-data-aided carrier frequency offset estimation of GMSK signals in burst transmissions[C]//2003 IEEE International Conference on Acoustics，Speech，and Signal Processing. Hong Kong，China，2003：576-579.

［6］ 田鹏武，袁 佳，于宏毅. 基于循环谱的MSK信号参数估计[J]. 通信技术，2008，41(1)：9-11.

Tian Pengwu，Yuan Jia，Yu Hongyi. Spectral-correlation analysis and parameter estimation of MSK signal[J]. Communications Technology，2008，41(1)，9-11(in Chinese).

［7］ Magana M E，Kandukuri A. Non-data-aided parametric-and nonparametric-based carrier frequency for burst GMSK communication systems[J]. IEEE Transactions on Instrumentation and Measurement，2010，59(7)：1783-1792.

［8］ Kay S. A fast and accurate single frequency estimator [J]. IEEE Transactions on Acoustics，Speech，and Signal Processing，1989，37(12)：1987-1990.

［9］ Fitz M. Planar filtered techniques for burst mode carrier synchronization[C]//IEEE Global Telecommunications Conference GLOBECOM '91：Countdown to the New Millennium. Phoenix，USA，1991：365-369.

［10］ Wang Cuilian，Li Yin，Li Ke. An high-precision FFT frequency offset estimation algorithm based on interpolation and binary search[C]//2019 IEEE 3rd Information Technology，Networking，Electronic and Automation Control Conference(ITNEC). Chengdu，China，2019：437-442.

［11］ 孙宏军，王小威. 基于幅值-相角判据的修正Rife正弦波频率估计算法[J]. 天津大学学报：自然科学与工程技术版，2018，51(8)：810-816.

Sun Hongjun，Wang Xiaowei. Modified rife algorithm for frequency estimation of sinusoid wave based on amplitude and phase criterion[J]. Journal of Tianjin University：Science and Technology，2018，51(8)：810-816(in Chinese).

［12］ Rife D C，Vincent G A. Use of the discrete Fourier transform in the measurement of frequencies and levels of tones[J]. Bell System Technical Journal，1970，49(2)：197-228.

［13］ Quinn B G. Estimation of frequency，amplitude，and phase from the DFT of a time series[J]. IEEE Transactions on Signal Processing，1997，45(3)：814-817.

［14］ 邓振淼，刘 渝，王志忠. 正弦波频率估计的修正Rife算法[J]. 数据采集与处理，2006，21(4)：473-477.

Deng Zhenmiao，Liu Yu，Wang Zhizhong. Modified Rife algorithm for frequency estimation of sinusoid wave[J]. Journal of Data Acquisition & Processing，2006，21(4)：473-477(in Chinese).

［15］ Candan C. A method for fine resolution frequency estimation from three DFT samples[J]. IEEE Signal Processing Letters，2011，18(6)：351-354.

［16］ Suleiman D U，Niknoordini N，Mazlina E，et al. Real-time frequency estimation of complex GMSK signal of green[J]. Journal of Electronic Science and Technology，2016，14(2)：126-132.

High-Precision Frequency Offset Estimation Algorithm for Single-Carrier GMSK Modulation Signals

Gao Jing1, 2，Sang Tian1, 2，Luo Tao3

(1. School of Microelectronics，Tianjin University，Tianjin 300072，China；2. Tianjin Key Laboratory of Imaging and Sensing Microelectronic Technology，Tianjin 300072，China；3. College of Intelligence and Computing，Tianjin University，Tianjin 300350，China)

In receiver, the accuracy of frequency offset estimation determines the accuracy of signal demodulation. GMSK modulation is one of the modulation methods for deep space communication. The complex space environment brings great challenge to the realization of high-precision frequency offset estimation. In this study, a high-precision interpolation estimation algorithm based on fast Fourier transform (FFT) is proposed to further improve the accuracy of GMSK signal frequency offset estimation. The algorithm is a non-data-aided algorithm, which does not need to rely on pilot frequency information, and can be used with the data-aided algorithms. In the transmission process of GMSK signal, the complex atmospheric environment leads to a very low signal-to-noise ratio transmission channel. In the low SNR channel environment, the estimation algorithm needs to improve its anti-noise capability to achieve the desired accuracy. In this paper, the high-precision interpolation estimation algorithm first performs FFT operation on the received signal, obtains the spectrum information of the received signal, and realizes the preliminary estimation of the signal frequency. After that, the maximum FFT spectral line is compared with the spectral line value at the center of its adjacent spectral line, and the point with maximum FFT value is taken as the peak spectral line. Finally, the estimated frequency offset is obtained by mathematical calculation of the peak spectral line. Simulation results show that the proposed algorithm has better estimation accuracy than other existing algorithms, has a more stable estimation effect, reduces the signal-to-noise ratio threshold, and can be used for the carrier frequency offset estimation of GMSK signals in various environments.

frequency offset estimation；fast Fourier transform；low signal to noise ratio threshold；high-precision

TN914

A

0493-2137(2020)12-1301-07

10.11784/tdxbz201910041

2019-10-23；

2019-11-11.

高 静（1979— ），女，博士，副教授.

罗 韬，luo_tao@tju.edu.cn.

天津市科技计划资助项目(17ZXRGGX00030)．

Supported by Tianjin Science and Technology Project(No. 17ZXRGGX00030)．

(责任编辑：王晓燕)