逐步增加Ⅱ型截尾下复合瑞利分布参数的Bayes估计

邵媛媛 周菊玲 董翠玲

( 新疆师范大学数学科学学院，830017，乌鲁木齐 )

1 引 言

复合瑞利分布是将三参数Burr-Ⅻ分布中其中一个参数固定的一类分布.由于复合瑞利分布在社会学、经济学和环境学等方面发挥着重要的作用，因此对该分布研究较为必要.文献[1]对复合瑞利分布进行可靠性分析；文献[2]在完全数据情况下对复合瑞利分布的尺度参数进行研究.当进行寿命试验时通常研究缺失数据,其中针对逐步增加II型截尾数据进行统计推断研究已有大量成果,例如文献[3-5]在逐步增加II型截尾样本下对串联系统的可靠性分析进行研究,文献[6-14]在逐步增加Ⅱ型截尾样本下,对Burr-Ⅻ分布、Lomax分布、Pareto分布和广义指数分布进行研究.

在逐步增加Ⅱ型截尾样本下,针对复合瑞利分布的尺度参数尚没有见到,本文将针对这一问题进行讨论.

根据文献[15，16],复合瑞利分布的分布函数为

F(x;θ,λ)=1-λθ(λ+x2)-θ，x>0,θ,λ>0，

(1)

其密度函数为

f(x;θ,λ)=2θλθx(λ+x2)-(1+θ)，x>0,θ,λ>0，

(2)

其中θ,λ分别被称为尺度参数和形状参数.

对较为昂贵的试验样品来说,寿命试验通常采用截尾试验,在试验过程中已有部分样品失效,考虑到试验时间、费用等因素,将产品进行逐步增加Ⅱ型截尾试验.

假设现从一大批服从复合瑞利分布(1)的产品中,随机抽取n个产品参加逐步增加Ⅱ型截尾试验.

根据上述试验,令x=(x1,x2,…,xm),假设R1,R2,Rm,事先给定.由文献[4]可得,样本的似然函数为

(3)

本文将在形状参数已知的情况下讨论尺度参数的估计.

定理1在逐步增加Ⅱ型截尾样本寿命试验中,复合瑞利分布(1)中尺度参数θ的极大似然估计存在，并且该估计是唯一的.

证由于

3 尺度参数θ的Bayes估计

下面在形状参数λ已知的情况下讨论尺度参数的Bayes估计.

3.1无先验信息下尺度参数的Bayes估计易知下式成立：

根据Jeffreys先验信息准则可取参数θ的先验分布为

(4)

根据上述试验可以得到样本的似然函数(3)与先验分布(4)式,由Bayes公式可以得到θ的后验密度函数为

其中Γ( )为伽马函数.

证由于在平方损失函数下,参数的Bayes估计为后验分布的均值,可知

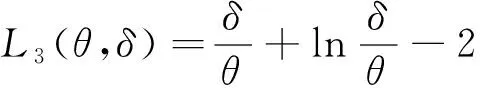
证后验风险函数为

3.2共轭先验分布取伽马分布时,参数θ的Bayes估计若取尺度参数θ的先验分布为Ga(α,β),其密度函数为

(5)

其中θ>0,超参数α>0,β>0.

由样本似然函数(3)式与先验分布(5)式,根据Bayes公式可得到θ的后验密度函数为

证由于在平方损失函数下,参数的Bayes估计为后验分布的均值,因此

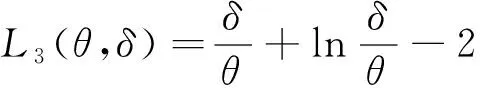
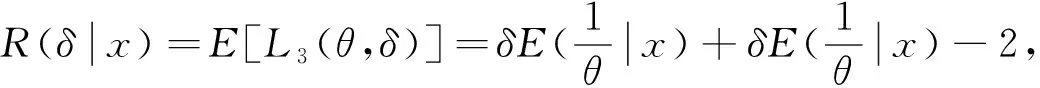
3.3先验分布为指数分布,参数θ的Bayes估计若取尺度参数θ的先验分布为指数分布,则其密度函数为

π3(θ)=μe-μθ，

(6)

其中θ>0,超参数μ>0.

由样本似然函数(3)与先验分布(6)式,根据Bayes公式可得到θ的后验密度函数为

证由于在平方损失函数下,参数的Baye估计为后验分布的均值,可知

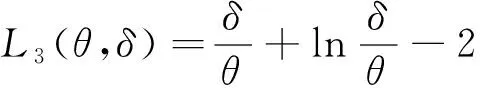
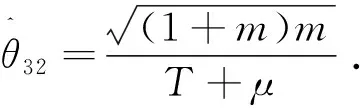
4 超参数μ的估计

由于定理6与定理7中含有超参数μ,因此需要使用文献[14-16]中的极大似然估计来估计μ.易知

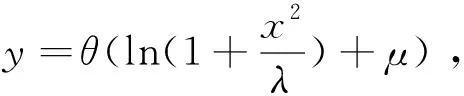
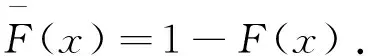
现在将未知参数转化为μ,利用f(x;μ),F(x;μ),则似然函数为

由于g1,g2在(0,+)上为严格递减的凹函数,所以

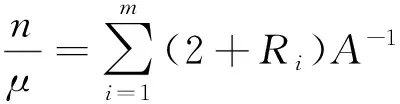
(7)

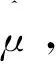
5 随机模拟

利用R软件随机模拟的方法产生一个服从复合瑞利分布(1)的逐步增加Ⅱ型截尾样本,具体步骤如下：

1) 产生一个容量为20且服从均匀分布U(0,1)的独立同分布样本U1,U2,…,Un;

3) 若取定

R1=[0,1,0，0，0，0，0，1，0，1，0，0，0，1，0，0，0，1，0，0],

R2=[0,1,0，0，1，0，0，0，0，0，0，0，0，1，0，0，1，0，1，0]，

R3=[0,0,1，1，0，0，0，0，1，0，0，0，0，0，1，0，0，0，0，1],

以及α= 2,β=1,μ=2.23,则样本数据可以得到,并且根据定理1至定理7可以得到不同损失函数下参数θ的估计值.以上过程重复1 000次,并计算均值和均方误差，模拟结果见表1．

表1 均值和均方误差