一维分数阶Cattaneo方程的紧致差分格式

王小菡 姜子文

( 山东师范大学数学与统计学院，250358，济南 )

1 引 言

Cattaneo方程是用来描述具有有限传播速度的扩散过程的一类方程.Compte等人[1]从三种不同的角度推广Cattaneo方程,得到了三种不同形式的Cattaneo模型.Ghazizadeh等人[2]提出分数阶Cattaneo模型显式有限差分法和隐式有限差分法.Povstenko[3]研究了时间分数阶Cattaneo型方程,建立了相应的热应力理论.Li Xiaoli等人[4]研究了分数阶Cattaneo方程的块中心有限差分法.

本文考虑如下形式的推广分数阶Cattaneo方程

(1)

u(x,0)=φ(x),ut(x,0)=ψ(x),x∈(0,L),

(2)

u(0,t)=μ(t),u(L,t)=υ(t),t∈[0,T]，

(3)

定义1[5]设α是一个正实数,令n-1<α≤n,n为一个正整数.函数f(t)定义在区间[a,b]上，称

2 记号及引理

对于任意的网格函数u∈Uh,引进如下记号

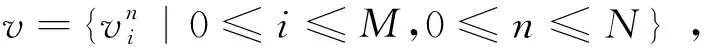
记

定理1[5]设f(t)∈C2[t0,tn],0<α<1,则有

其中|R(f(tn))|为逼近误差.

定理2[6]设f(t)∈C3[t0,tn],1<β<2,则有

3 差分格式的构造

在结点(xi,tn)处考虑微分方程(1)-(3)有

(4)

对相邻的两个时间层取平均[6]，可得

(5)

对(5)式两端作用紧算子A,并对时间分数阶导数采用L1逼近公式离散可得

(6)

(7)

由边值条件(2)-(3)，可得

(8)

(9)

(10)

(11)

(12)

4 数值算例

本节将给出具体算例来说明格式(10)-(12)的误差阶.

算例1考虑如下Cattaneo问题

u(x,0)=φ(x),ut(x,0)=ψ(x),

u(0,t)=0,u(L,t)=0.

取对应的精确解u(x,t)=t2sinπx,则函数f(x,t)和初边值条件可由u(x,t)得到.各系数分别取D=1,α=0.3,ε=0.1.计算结果分别如表1、表2所示.在表1中取时间步长Δt=1/128,在表2中取空间步长h=1/30 000.

表1 关于不同空间步长的收敛阶

表2 关于不同时间步长的收敛阶

通过数值算例可以看出,对于不同的空间步长,空间误差阶达到了四阶;对于不同的时间步长，时间误差阶达到了2-α阶,从而验证了本文所建立格式的有效性.