基于空间自回归神经网络模型的空间插值研究

曾金迪，张丰*，吴森森，杜震洪，刘仁义

（1.浙江大学 浙江省资源与环境信息系统重点实验室，浙江杭州310028； 2.浙江大学 地理信息科学研究所，浙江 杭州310027）

空间插值是空间统计分析中的热门研究领域[1]。在空间研究区域内，由于存在不可观测的位置，或难以大面积铺设监测站点，导致产生大量未知数据点。依据地理学第一定律[2]：“任何事物都是与其他事物相关的，只不过相近的事物关联更紧密”，尝试通过已知点，对研究区域内的未知点进行空间插值[3-4]。因此，如何有效表征事物在空间范围内的分布，反映其空间变化趋势与内在规律，成为空间插值的重点与难点。

空间插值方法主要有两种：一种是确定性方法，即基于样本点之间的相似程度或者平滑程度构建拟合曲面，预测未知点数据，如反距离权重（IDW）法[5]、趋势面法以及样条函数法等；另一种是地统计方法，即利用样本点变量随空间位置变化的规律，使样本点之间的空间自相关性定量化，从而在待预测点周围构建样本点的空间结构模型，预测整个空间区域情况，如克里金（Kriging）插值法[6-7]。空间插值被广泛应用于降雨分布规律预测[8]、土地污染评估[9]、空气质量研究[10]、物质浓度分布[11]等领域。

空间插值的本质是建立样本点和待预测点之间的自相关关系[12-13]，即

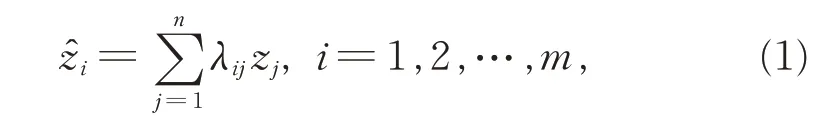
其 中，ẑi为 待 预 测 点 的 估 计 值，zj为 第j个 样 本 点 的观测值，λij为权重系数，其求解方法可影响预测结果的准确性。不同插值方法其权重求解策略不同，例如IDW 法以空间距离幂次方倒数的加权平均作为空间权重系数，Kriging 法用变异函数计算权重，而变异函数又与空间距离有关[14]，可统一表示为权重系数λij和空间距离之间的非线性关系，即

传统空间插值方法如反距离权重和半变差函数等在一定程度上拟合了权重与空间距离的相互关系，但由于其需要一定先验假设条件，求解模型相对简单，难以精准计算权重与空间距离间的复杂非线性关系，易造成“牛眼”和锯齿现象，过渡处平滑性欠佳，影响插值效果。近年来，神经网络的兴起为空间插值提供了新思路。由于神经网络对复杂系统具有强大的非线性建模和分析能力[15]，已有学者将其应用于空间插值并取得了良好的效果。李纯斌等[16]建立了以经纬度、高程为输入，降雨量为输出的BP 神经网络，并与支持向量机（SVM）方法进行比较；邱云翔等[17]用粒子群算法优化BP 神经网络，并将其应用于流域降水空间插值，提高了模型的稳定性，但缺乏对空间权重的考虑；SOARES 等[18]对传统方法进行了优化，基于原始增量高斯混合网络（IGMN），提出了IGMN 神经网络模型，并将其应用于模拟数据插值研究，在保持空间相关性的同时兼顾空间异向性，但数据需满足高斯分布；ZHU 等[19]提出了条件生成对抗神经网络（CEDGANs）模型，即由生成器生成伪样本，用判别器对伪样本进行修正，并对珠江三角洲等4 个地区的DEM 数据进行了插值研究，该模型对地形解释能力较强，但对迁移的解释能力有待验证，且模型较复杂。

综上所述，现有基于神经网络的空间插值方法提高了插值精度，针对已有方法的优化，或是直接拟合得到未知数据与已知数据间的非线性关系，模型较为复杂，缺乏对空间相关权重的精准解算。而传统空间插值方法需先验假设条件，模型相对简单，但难以精准拟合权重与空间距离间的相互关系。因此，针对式(2)中权重系数与空间距离间的非线性拟合问题，本文将空间神经网络应用于权重系数求解，提出了一种空间自回归神经网络（SARNN）模型，并将其应用于空间插值，对两类模拟数据和海洋环境数据进行了交叉验证，并将传统的反距离权重法和普通克里金法进行了比较。

1 空间预测模型

1.1 IDW 法

IDW 法以未知点和样本点之间的空间距离为权重进行加权平均，距离越近权重越大，其权重贡献与距离成反比，计算公式为

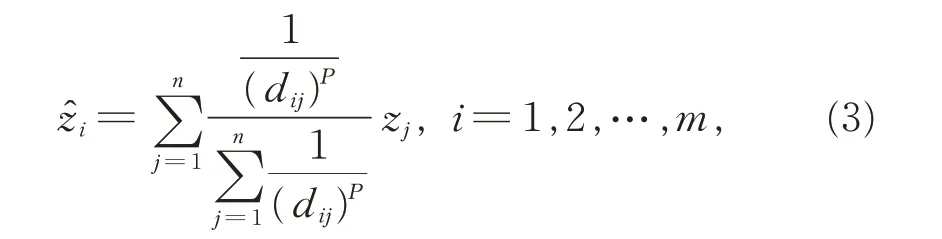
其 中，ẑi为 未 知 点 的 估 计 值，zj为 第j个 样 本 点 的 观测值，dij为待插值点i和第j个样本点之间的欧式距离，P为幂指数，通常取2。IDW 法简单方便，效果直观，被广泛应用于地理、环境、农业、海洋等领域，但样本点中的极端值对空间预测结果影响较大。

1.2 普通克里金法

克里金法包括普通克里金法、泛克里金法、协同克里金法等，其中普通克里金法（ordinary Kriging，以下称Kriging 法）最为常用。Kriging 法利用空间研究区域内已知点的数据，由变异函数计算最佳权重系数，从而对未知点进行线性无偏估计。Kriging法的计算公式为

为了满足估计值的无偏性与最优性，设z*(x0）为z(xi)的无偏估计，E[z*(x0)]=E[z(xi)]为估计值的最小方差，即Var(z*(x0)-z(xi))，建立以下方程组计算权重系数λi：

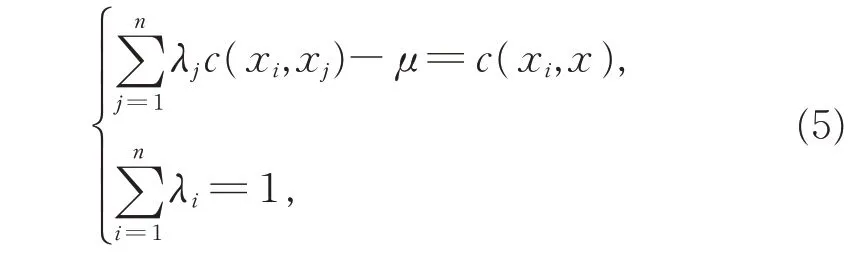
其中，μ为拉格朗日乘数，c(xi,xj）为样本点与样本点间的协方差函数，c(xi,x)为样本点与未知点间的协方差函数。考虑样本点在空间研究区域随机分布的特点，Kriging 法选取不同的变异函数，如球形函数模型、指数函数模型等进行权重计算，变异函数的选择影响预测精度。

1.3 空间自回归神经网络模型

传统空间插值方法其核心是基于空间自相关关系，建立权重系数与空间距离之间的非线性函数。基于此，本文构建了一种融合神经网络的空间自回归（spatial auto-regressive neural network，SARNN）模型。

1.3.1 模型算法

对式(1)，IDW 法以空间距离幂次方倒数的加权平均作为空间权重系数，得到式(3)；Kriging 法则利用变异函数计算权重，其与空间距离相关，得到式(5)。两者均需建立权重系数λij和空间距离间的非线性关系。

由于待预测点与已知样本点的空间权重系数与其到已知样本点之间的距离有关，定义空间权重系数λi与空间距离d的非线性函数如下：

其中，wij为第i和第j个点之间的空间权重，dsij为第i和第j个点之间的空间距离。同时，训练时为了防止自拟合，待预测点与自身之间的空间权重应当为0，即

因此，根据式(6)和式(7)，定义

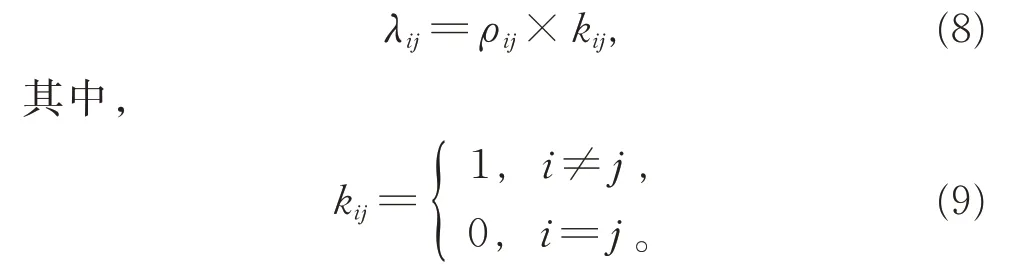
从而确保模型训练过程中样本点的估计值与自身无关。为了表征权重系数与空间距离之间的非线性关系，利用神经网络强大的分析建模能力，设计空间神经 网 络（spatially neural network，SNN）对ρi=(ρi1,ρi2,…,ρin)进行非线性拟合，SNN 用样本点之间的空间距离作为网络输入，适当设置隐藏层并以空间权重系数分量ρi作为网络输出，即

其中，[]T代表第i个样本点到所有样本点之间的距离。将通过空间神经网络训练得到的空间权重系数分量ρij与kij相乘，得到两点之间的权重系数λij，其矩阵形式为

将权重矩阵λ 与已知的观测数据相乘，得到样本值的估计结果：

1.3.2 模型流程设计与训练流程设计

采用十折交叉验证法进行模型训练与验证。将样本点分为10 等份，随机选取9 份作为训练集、1 份作为验证集。在训练过程中，模型的输入为训练集中样本点的空间距离矩阵，损失函数为均方误差（MSE），通过SNN 得到空间权重分量ρ，再与权重分量k 和已知点的观测值y 相乘得到未知点的预测值，并进行精度检验。模型流程如图1 所示。

为了提高模型的训练效率和精度，设计了一套训练流程。首先，用Early Stop 方法防止过拟合，当训练集的MSE 继续下降，验证集的MSE 开始上升时，提前终止训练；其次，用dropout 层随机隐藏部分神经元，以提高模型泛化能力并避免过拟合[20-21]；此外，对神经网络的每层，用PReLU 作为激活函数[22-23]；最后，采用batch-normalization 技术[24]通过变化的学习步长进行训练。训练流程如图2 所示。

1.4 模型评价标准

将决定系数R2、均方根误差RMSE、平均绝对误差MAE、平均相对误差MAPE 作为模型精度的评定标准，计算公式如下：

图1 模型流程Fig.1 The process of mode l

图2 训练流程Fig.2 Training process

2 模拟验证

2.1 数据模拟

为了验证在不同空间环境下模型的效果，参考HARRIS 提出的空间数据模拟方法[25]，分别定义了2种模拟数据：一般的空间自相关数据和突变的空间自相关数据。首先，定义一个12×12 单元的空间区域，在此区域中，共计有25×25=625 个样本点，垂直方向和水平方向相邻的2 个样本点的距离为0.5，样本点的空间坐标(ui,vi）按以下方式生成：

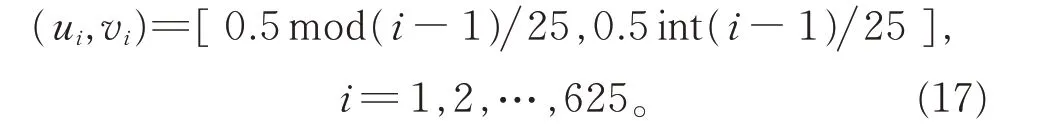
其次，在此空间区域，对2 类数据集进行模拟。（i） 模拟数据集1

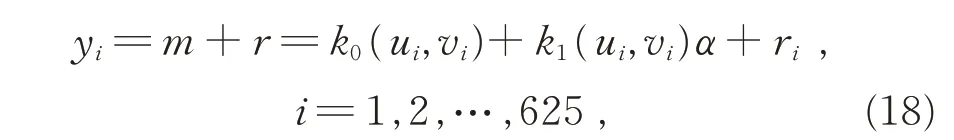
其中，m=k0(ui,vi)+k1(ui,vi)α为具有空间自相关性的趋势项，α～U(0,1)，k0，k1与空间位置有关：

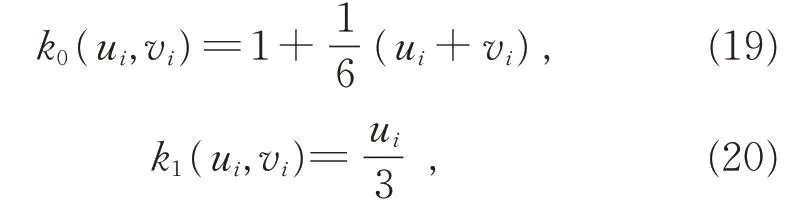
ri为具有空间自相关性的残差项，依据有基台的高斯模型生成：

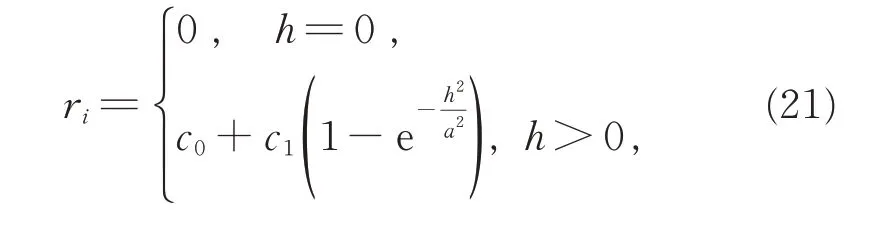
数据集1 的预测结果如图3 所示，预测散点分布如图4 所示。从图3（a）中可以看出，数据集1 的模拟结果总体呈从左上到右下渐变的趋势，具有一定的空间相关性。（ii） 模拟数据集2

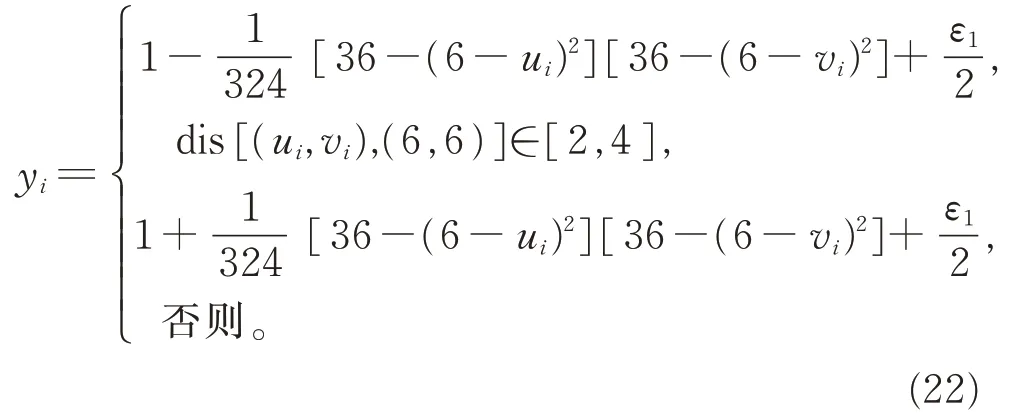
数据集2 的预测结果如图5 所示，预测散点分布如图6 所示。从图5（a）中可以看出，数据集2 的模拟结果较为复杂，既有与空间相关的数据，又有较强的空间突变数据。

最 后，对2 类 数 据 集 进 行Moran’I 检 验，结 果见表1。

由表1 可知，数据集1 和数据集2 具有较强的空间相关性，可以用于空间预测的验证。本文将2 类数据集分别随机分为10 等份，按照上文定义的模型进行训练。由于本文模型是一个f:n→n的映射，在综合考虑网络复杂度、模型平衡性与特征提取能力的基础上，设计了一个5 层的神经网络，包括1 个输入层、1 个输出层和3 个隐藏层。神经元数目过少会导致模型特征提取能力不足，过多则会增加网络的复杂程度，降低计算效率。因此根据SARNN 模型特点，当输入样本数为n时，可通过以下算法计算隐藏层神经元数目，提取样本特征。

表1 模拟数据集的Moran’I 检验结果Table 1 Moran’I of simulation data set

算法1隐藏层神经元数目的确定。

输入：训练数据样本数n；

计算过程：

1： fori=0 do

2： if 2i＞n

3： then 输出[2i，2i+1，2i]

4： elsei=i+1

5： end；

输出：隐藏层神经元数目。

模拟数据集训练网络的结构和超参数设置如表2 所示。

表2 模拟数据集训练网络的结构和超参数Table 2 Structure and super parameters of simulation data set training network

2.2 验证结果与讨论

IDW 法、Kriging 法以 及SARNN 法的交 叉验证结果如表3 所示。从预测结果的精度上看，SARNN法误差最小，效果最好。对于数据集1，SARNN 法的R2由IDW 法 的0.752 5 和Kriging 法 的0.710 2 提升至0.782 7，分别提升了4.01%和10.21%，RMSE由IDW 法 的0.008 4 和Kriging 法 的0.010 0 降 至0.007 4，分别降低了11.90%和26.00%，在MAE 和MAPE 上，SARNN 法 相 对 于IDW 法和Kriging 法也有一定程度的改善；对于数据集2，SARNN 法预测效 果 更 好，R2由IDW 法 的0.707 2 和Kriging 法 的0.718 2 升 至0.896 8，分 别 提 升 了26.81% 和24.87%，RMSE 由IDW 法 的0.016 2 和Kriging 法 的0.014 8 降 至0.005 5，分 别 降 低 了66.05% 和62.83%，在MAE 和MAPE 上，SARNN 法 相 对 于IDW 法和Kriging 法也有较大改善。

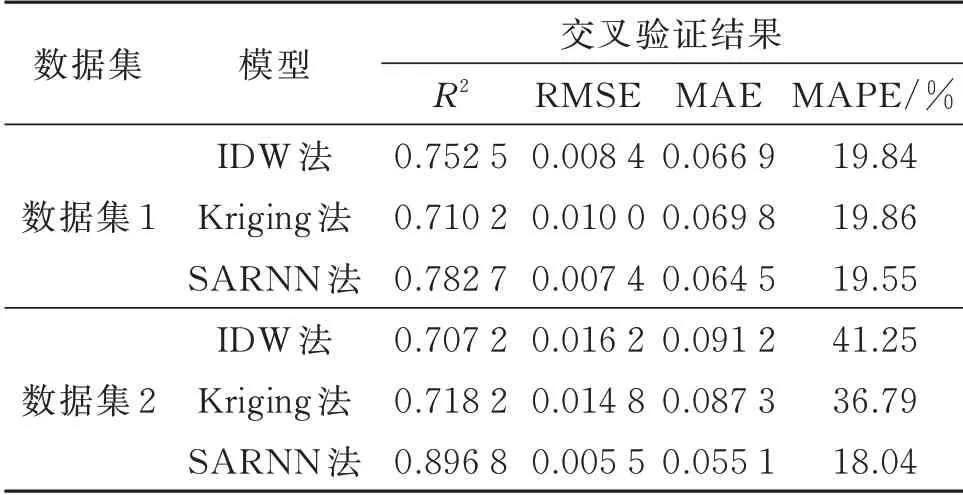
表3 模拟数据集交叉验证结果Table 3 Cross validation results of Simulation data set

IDW 法、Kriging 法和SARNN 法 基于模 拟数据的空间预测结果和预测散点图如图3～图6 所示。从预测结果看，对于数据集1，SARNN 法在较高值和较低值的预测上更精准，预测的整体趋势面过渡较为平滑，没有出现明显的突变和锯齿；对于数据集2，SARNN 法对突变空间数据的预测更精准，在突变处未出现明显的过渡带，这是由IDW 法和克里金法对突变位置两侧的数据取平均造成的预测偏差。

总体而言，利用神经网络，SARNN 法能够较好地拟合空间预测模型中权重与空间距离之间的复杂非线性关系，在权重计算与空间数据突变处理上具有一定优势。

图3 数据集1 的模拟结果Fig.3 The simulation results of data set one

图4 数据集1 散点图Fig.4 Scatter of data set one

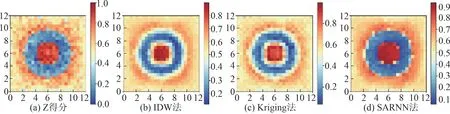
图5 数据集2 的模拟结果Fig.5 The simulation results of data set two

3 基于海洋环境数据的实证分析

3.1 研究区域与数据

以浙江省近岸海域为研究区，区域北界从浙沪交界向海延伸至外海领海界限，区域南界从浙闽交界向东延伸至外海领海界限，总面积约4.44 万km2。本文选取浙江省近岸海域的海洋环境监测数据的磷酸盐（）因子作为研究对象。作为水体富营养化的主要原因之一，研究其空间分布对于水体治理和保护具有重要意义。数据来自浙江省海洋监测预报中心，对数据进行清洗、去噪，得到2016 年5月浙江省近岸海域的监测数据，共计314 条，数据集分布如图7 所示。从图7 中可以看出，数据集总体上呈现北高南低、西部沿岸高东部海域低的空间分布特性。

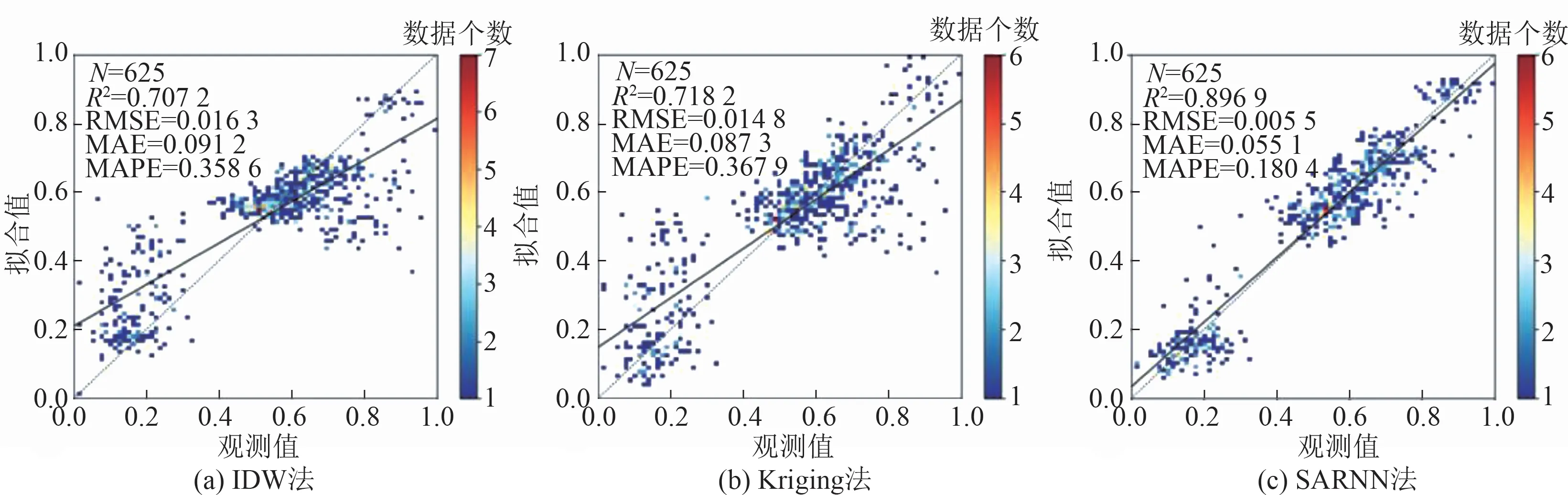
图6 模拟数据集2 散点图Fig.6 Scatter of simulation data set two

图7 数据集空间分布Fig.7 Spatial distribution of data sets

表4数据集的Moran’I检验结果Table4Moran’I of data sets

表4数据集的Moran’I检验结果Table4Moran’I of data sets

数据集PO4 2-Moran’I 0.503 4 Z 得分24.104 4 P 值0.000 1

3.2 实证分析的结果与讨论

所示。相关系数R2从大到小依次为SARNN法、3种模型对数据的交叉验证结果如表6 IDW 法与Kriging 法，其中SARNN 法的相关系数最高，为0.857 8，说明其插值结果与观测值的空间一致性较好，从RMSE、MAE 和MAPE 看，SARNN 法的精度较IDW 法和Kriging 法有较大改善，其中RMSE 法 由IDW 法 的1.28×10-4和Kriging 法 的2.18×10-4降至0.86×10-4，分别降低了48.83%和60.55%，说明SARNN 法误差较小，预测更精准。

表5 数据集训练网络的结构和超参数设置Table 5 Structure andsuperparametersof trainingnetwork

表5 数据集训练网络的结构和超参数设置Table 5 Structure andsuperparametersof trainingnetwork

神经网络超参数输入层314最大学习率0.6隐藏层1 512最小学习率0.05隐藏层2 1 024最大迭代次数20 000隐藏层3 512批量64输出层314退出0.75

在杭州湾、台州湾等沿岸区域，低值区出现在西部海域及南部浙闽交界处。其中，IDW 法生成的插值结果出现了较为明显的“牛眼”现象，这是其计算原理导致的；Kriging 法生成的PO42-空间分布图存在大量局部锯齿，插值精度较低，可观性较差。相比之下，SARNN 法插值精度较高，在台州湾、杭州湾等高值区域以及浙闽交界处等低值区域的插值结果更准确，整体空间范围内的插值结果更平滑，趋势面过渡平稳渐进，空间分布效果较好，但一些空间监测站点也存在小圆区域，这是样本数据与周围数据跨度较大导致的。

表6 交叉验证结果Table 6 Cross validation results of data set

表6 交叉验证结果Table 6 Cross validation results of data set

数据集PO4 2-模型IDW 法Kriging 法SARNN 法交叉验证结果R2 0.798 1 0.649 4 0.857 8 RMSE 1.28×10-4 2.18×10-4 0.86×10-4 MAE 0.007 4 0.008 9 0.006 7 MAPE 0.656 6 0.777 3 0.468 3

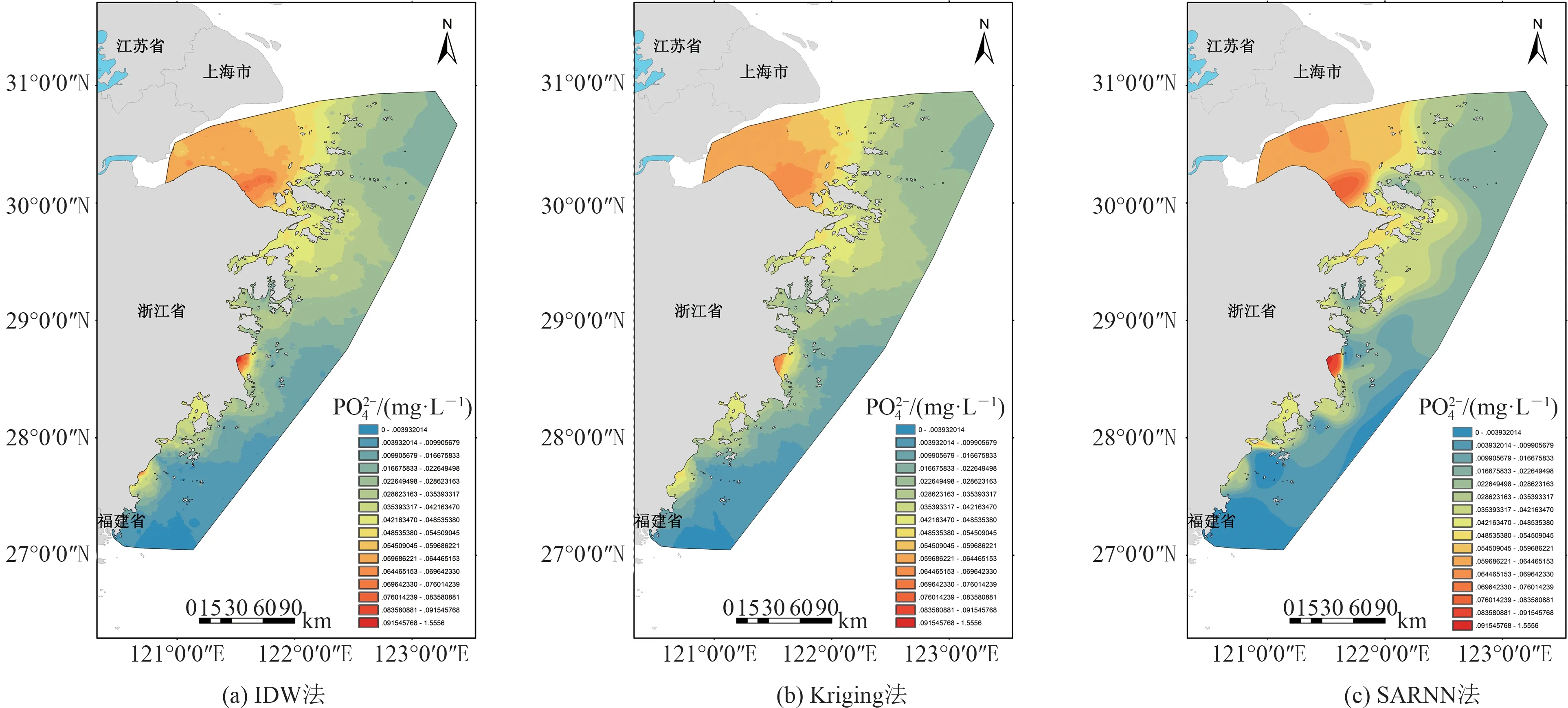
图8 插值结果Fig.8 Interpolation results of

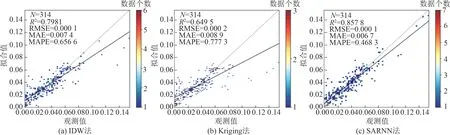
图9 散点图Fig.9 Scatter of

4 结 语

在传统空间插值方法中，权重与空间距离的求解需先验条件，且模型简单，难以表征其复杂的非线性关系，而现有基于神经网络的插值方法通过直接拟合已知与未知数据间的关系，忽略了空间自相关权重。针对以上问题，本文建立了一种空间自回归神经网络（SARNN）模型，将其应用于空间插值，对两类数据集和实测数据集分别进行了交叉验证，并与传统的IDW 法和Kriging 法进行了比较。

交叉验证结果表明，在空间插值精度上，SARNN 法整体优于IDW 法与Kriging 法，但不同数据集的空间插值效果不同。在统计指标上，SARNN 法的相关系数R2和均方根误差RMSE 均优于IDW 法和Kriging 法，在其他统计指标，如MAE、MAPE 上，SARNN 法也有较大改善。

空间插值结果表明，SARNN 法更适合进行空间数据的平滑性建模和对突变数据的预测，能较好消除“牛眼”锯齿等现象，更能表征事物在空间上的变化趋势。SARNN 法充分利用了神经网络对样本特征的学习拟合能力，将空间插值问题转化为神经网络的优化拓扑问题，在一定程度上解决了传统插值方法对权重与空间距离间复杂非线性关系拟合欠佳的问题，模型相对简洁，具有一定的适用性和推广性。但对于大面积数据缺失的情况，SARNN 法尚待进一步验证。