基于遗传小波神经网络的停车泊位预测方法
韩锟,李斯宇
基于遗传小波神经网络的停车泊位预测方法
韩锟,李斯宇
(中南大学 交通运输工程学院,湖南 长沙 410075)
在车位共享模式下,对社区停车位进行短时、准确地预测,既有利于停车需求方选择更合适的车位,也有利于车位资源的合理分配。提出一种社区停车位的短时预测方法,首先利用C-C方法对空余停车泊位时间序列进行相空间重构,采用李雅普诺夫指数法证明该时间序列的可预测性;然后将重构后的时间序列输入小波神经网络(wavelet neural network, WNN)进行训练。采用遗传算法(genetic algorithm, GA)优化小波神经网络初始参数,经过多次迭代获取最优参数,得到优化后的预测模型;最后,通过matlab对该算法进行编程,并调研长沙市某社区空余停车泊位数据进行实验分析。研究结果表明:基于相空间重构的遗传小波神经网络(CC-GA-WNN)模型具有较好的预测精度和优化效果。
空余停车泊位;相空间重构;遗传算法;小波神经网络
2018年初,成都市政府发布了《关于鼓励和支持停车资源共享利用工作的实施意见》,鼓励和支持社区私家车位的错时租赁。截至19年8月,私家车位APP在成都已入驻300余个楼盘,得到龙湖、华润等一线物业的广泛认可。共享车位模式一方面可以应对停车位资源的日益紧张,缓解停车难问题;另一方面,出租车位的业主可以通过租赁闲时车位获取一定的收益。然而,目前很多停车诱导工具都是实时显示当前空余车位的数量,当驾驶者到达停车场后,空余车位数量往往会发生变化,经常会出现“扎堆”停车的状况。对车位数量做出短时预测,可以更加有效地分配车位资源,避免区域停车需求过饱和的情况,肖飞等[1]对无锡市某区域的停车需求进行短时预测并合理分配车位资源,结果有效地分散了停车高峰需求,该区域的停车高峰需求总量减少了20%,使不同停车区域间的泊位利用率得到有效提升。同时,人们通常更需要了解在未来某个时间某停车场有多少空余停车位,以便驾驶者更好地规划行程。近年来,随着人工智能的发展,LSTM神经网络模型[2−3]、小波神经网络模型等[4−6]被广泛运用于短时停车泊位数量预测领域。陈群 等[7−8]均采用相空间重构技术与Elman神经网络进行融合的方法,区别在于陈群等[7]采用自相关函数法进行相空间重构,段满珍等[8]采用非线性的C-C方法进行重构。实验表明,2种方法的预测结果与实际值均具有较好的一致性,平均相对误差均在3%以内。从预测精度上看,段满珍等[8]采用的C-C方法可以更好地反映小数据样本的非线性特性,具有更好的预测效果;张金梦等[9]构建了遗传算法优化BP神经网络的有效泊车位数量预测模型,并对该模型进行训练,结果显示该方法有效提高了BP神经网络的稳定性,避免其过早地陷入局部最优,从而提高了停车泊位的预测精度,从实验结果对比中,可以看出进化算法优化的神经网络在预测精度和稳定性上有较大提升;陈海鹏等[10−11]均对空余停车泊位构成的时间序列进行小波分解和重构,在神经网络的选择上,陈海鹏等[10]采用ELM网络对分解后的时间序列进行预测,并将各神经网络的预测结果进行合成,相比于小波神经网络、OS-ELM神经网络方法,该方法的预测均方差及训练速度均有了明显提高。季彦婕等[11]采用经粒子群优化的小波神经网络对分解后的时间序列进行预测,相比于未经智能算法优化的小波神经网络,其预测精度有大幅的提高,且呈现较好的稳定性。基于对以上文献的分析,可以得到以下几个结论:1) 停车泊位数构成的时间序列混沌特性较强,受到地理位置、天气、驾驶员习惯及心理因素等多方面的影响,预测难度较大。神经网络在混沌时间序列预测问题上表现出了较大的优越性,由以往的研究的预测结果看,可得到较好的预测精度。2) 商业停车场停车泊位多为商场自有车位,停车类型多为临时停车为主;社区停车场除业主自有车位外,还有部分物业持有待售的车位,允许部分外来车辆停车。因此,社区停车场的停车类型兼有固定车位停车和临时停车2种类型,其停车泊位数时间序列具有更丰富的内涵信息,一维时间序列难以反映其复杂特性,可以采用相空间重构的方法将单维时间序列拓展至多维,使其可以呈现出空余停车泊位数据中包含的更多信息。3) 与单独采用神经网络进行空余停车泊位数预测的方法相比,采用智能算法优化的神经网络可以得到更好的网络初始权值和阈值。使优化后的神经网络得到的预测结果与实际值具有更好的一致性。本文提出一种基于相空间重构的遗传小波神经网络的停车泊位短时预测方法。首先利用C-C方法[12]对停车泊位数构成的单维时间序列进行相空间重构,得到信息特征更显著的多维时间序列作为训练样本数据;然后利用遗传算法优化小波神经网络的初始权值和阈值,得到最优网络参数,构建优化后的小波神经网络停车泊位预测模型;最后采用长沙某停车场的空余停车泊位数据进行实验验证,对方法的有效性进行测试和验证。
1 空余停车泊位变化特性分析及相空间重构
1.1 空余停车泊位变化特性分析
在工作日状态下,由于社区居民的工作属性决定了居民早出晚归的作息特征,由此导致社区停车场空余停车泊位数呈现出一定的周期性及规律性。以长沙市某社区停车场2019年5月6日至5月10日间5个工作日的空余停车泊位数据为例,该停车场车位容量为500个,其空余停车泊位变化趋势如图1所示。可以看出,由于居民的“早出”特性,白天的社区存在大量的车位空置,具有较多的空余停车泊位;由于居民的“晚归”特性,夜间的社区车满为患,空余泊位数量较少,具备较强的规律性。同时各工作日全天的空余停车泊位变化趋势大致相同,表明空余停车泊位数在总体趋势上具有一定的周期性。

图1 某社区停车场工作日空余停车泊位变化曲线

从以上分析可以看出,虽然社区空余停车泊位时间序列在总体上具备一定的周期性,但其在早、晚高峰期间的波动率变化较大,呈现出较高的随机性,且波动的规律性较弱,随机性成分增大了准确预测的难度,而空余停车泊位时间序列这种一维的时间序列无法全面反映出复杂的动力学特性,因此需对一维时间序列进行相空间重构,将其映射为多维的时间序列,使其可以全面反映空余停车泊位数复杂的动力学特征和规律。
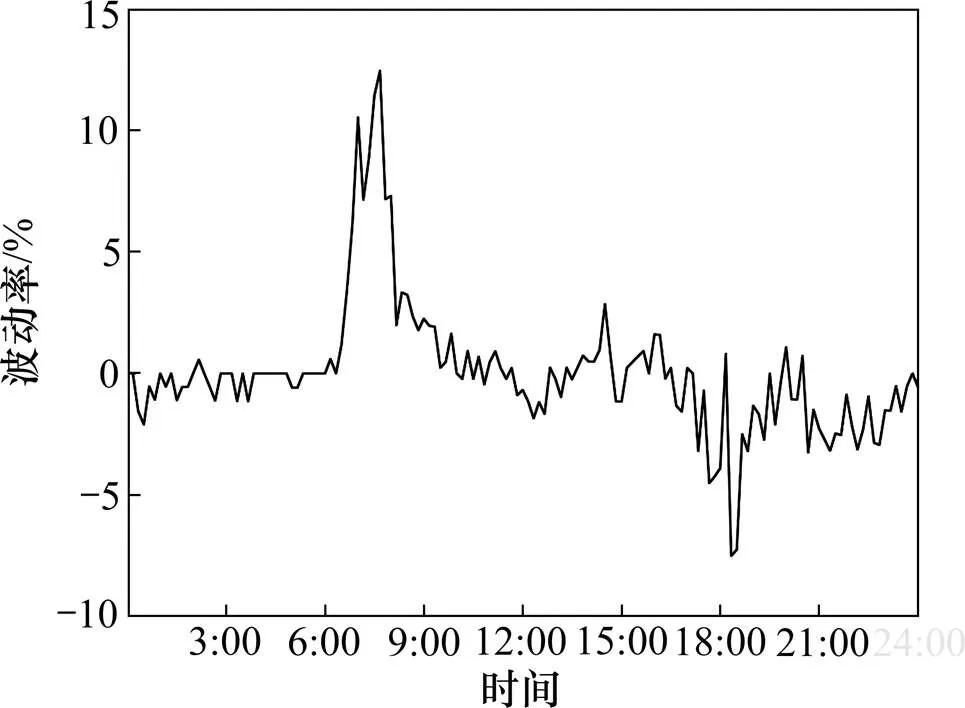
图2 停车场空余停车泊位数波动图
1.2 相空间重构及C-C方法
停车泊位数据构成的时间序列是一种具有较强非线性的混沌时间序列,其特性受地理位置、驾驶员心理等多方面因素的影响,而其数据表现形式为一维的时间序列,难以反映其复杂特性,因此需通过相空间重构的方法将其拓展至多维时间序列以映射出停车泊位数据中包含的多维信息。
对于一个长度为的一维停车泊位时间序列=(1,2,…,x),对其进行相空间重构得到多维时间序列

为嵌入维数,为时间延迟。由(1)式可知,相空间重构的关键是要选取合适的相空间重构参数:嵌入维数和时间延迟。
C-C方法融合了相空间重构理论中自相关函数、互信息法的优点,可以同时求出嵌入维数与时间延迟,有效减少了计算量,且在实际计算中对小数据组适应性较好。本文运用C-C方法实现一维时间序列向多维时间序列转换,具体步骤如下:
定义为时间序列的延迟,为延迟时间窗口,与关系如式(2)。

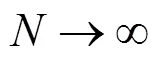
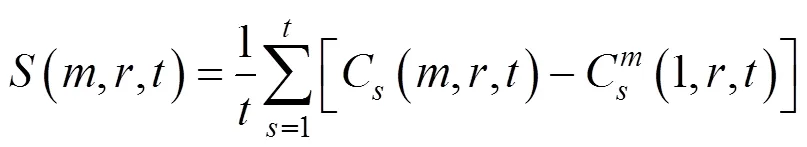
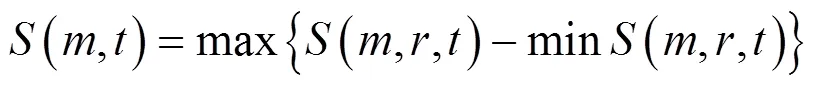
计算下列3式:
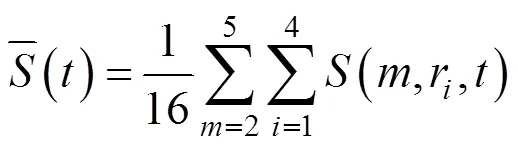


1.3 空余停车泊位序列混沌特性分析
对于一个混沌时间序列,可将其重构至高维空间以映射出数据更多的隐含信息,使其可预测性增强。对时间序列的混沌特性进行定量分析的方法有很多,本文采用李雅普诺夫(Lyapunov)指数法对空余停车泊位时间序列的混沌特性进行判定。最大李雅普诺夫指数λ的大小直接决定了该时间序列的动力学系统是否具有混沌特性。研究表明[14−15],若求得的最大Lyapunov指数λ大于0,则表明该时间序列具有混沌特性。本文采用在混沌时间序列预测中应用十分广泛的wolf法计算最大Lyapunov指数,具体步骤如下。
Step 1:将原始时间序列{1,2,…,x}利用C-C算法(本文采用)进行相空间重构,计算嵌入维数和时间延迟,得到重构后的时间序列:(t)={(t),(t+),…,(t+(−1))}。
Step 2:通过快速傅里叶变换方法计算时间序列中最强的频域分量,其对应的周期即为时间序列的平均周期。
Step 3:取初始点(0),其最近邻点为0(0),设两点间的距离为0,追踪两点的时间演化。
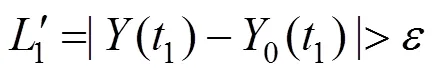
Step 5:继续进行Step 3,直至()到达时间序列终点,设为总迭代次数,由式(8)可求出最大Lyapunov指数。

2 遗传算法优化小波神经网络的空余停车泊位预测模型
遗传算法是模拟生物在自然环境下的遗传和进化过程的一种自适应的全局寻优算法,通过适应度函数、遗传中的选择、交叉和变异对个体进行筛选,使适应度好的个体被保留,适应度差的则被淘汰,如此往复循环,直至满足条件,寻到最优个体。利用遗传算法优化小波神经网络的初始连接权值和小波基函数参数,有利于跳出网络权值和阈值的局部最优解,获得全局最优解。该优化模型的流程如图3所示。
模型计算步骤如下。
Step 1:相空间重构。对待预测时间序列进行相空间重构,利用C-C方法求时间序列的嵌入维数,时间延迟常数,对重构后的时间序列进行归一化处理,作为网络的输入。
Step 2:网络初始化。确定网络拓扑结构,随机初始化小波神经网络的输入层到隐含层的网络权值u、隐含层到输出层的连接权值w、小波基函数的伸缩因子a以及平移因子b。

Step 4:计算适应度值。设种群中各个体的适应度为,为训练样本数,y为小波神经网络第个节点的期望输出,o为第个节点的预测输出。则个体适应度函数计算公式为
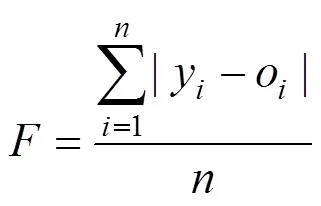
若适应度最大的个体满足精度要求或达到最大迭代步数,则转Step 8。
Step 5:选择操作。采用最常用的轮盘赌法。设F为个体的适应度值,为种群个体数目。通过设置代沟参数,将父代群体中适应度较低的个体舍去,即对父代个体进行选优,将选优后的个体置换原个体产生新一代群体,代购参数控制每代中种群被置换的比例。其个体的选择概率为

Step 6:交叉操作。采用实数交叉法,设为位于[0,1]之间的随机数,则第个染色a体和第个染色体a在位的交叉操作如下:
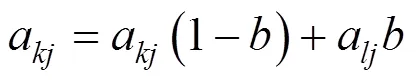

Step 7:变异操作。设max为基因a的上界,min为基因a的下界,为当前的迭代次数,max为最大进化次数,是位于[0,1]之间的随机数,2是随机数。则第个个体的第个基因变异操作如下:
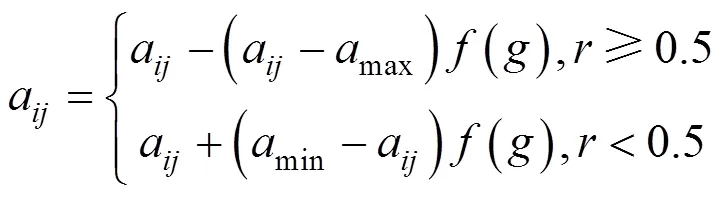

变异产生新的种群,转Step 4。
Step 8:将优化后的参数进行解码,作为网络的连接权值以及伸缩平移因子输入小波神经网络进行训练,采用梯度修正法修正权值和因子,使网络预测值逼近期望值,满足训练误差要求或迭代次数则终止训练,得到最终预测模型。
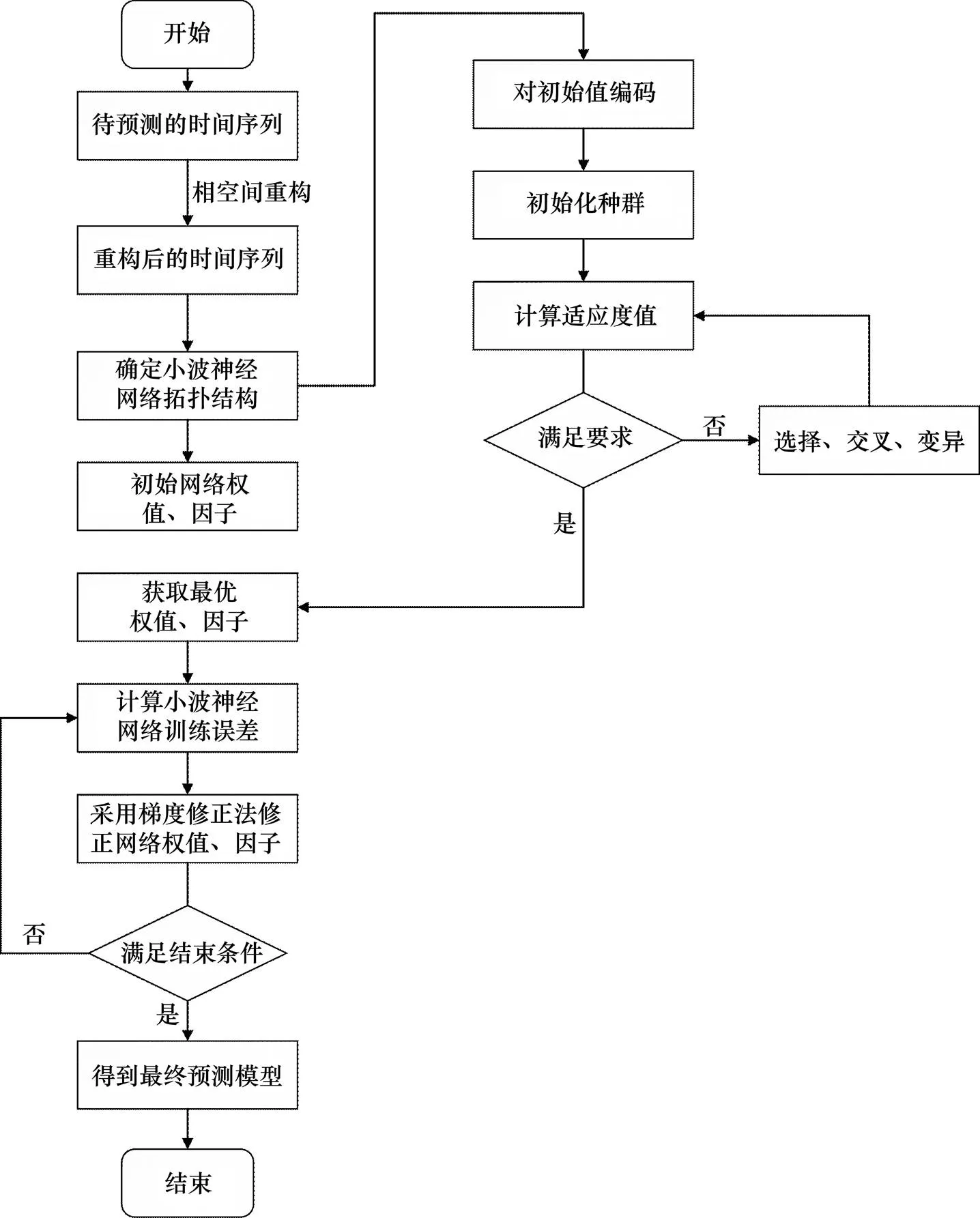
图3 遗传算法优化小波神经网络模型流程图
3 实验及结果分析
3.1 数据来源
为了对本文提出方法的有效性和实用性进行验证,实验采集了长沙市某社区停车场2019年5月6日(周一)至5月10日(周五)5个工作日的空余停车泊位数据来测试本文提出的预测方法。如果采样间隔过小,对于一个社区停车场而言,空余停车泊位数变化较小,呈现变化趋势不明显,会影响神经网络模型的训练效果。在对比了各采样间隔呈现的变化趋势后,本文选择以10 min为一个采样间隔来建立空余停车泊位的时间序列,使用前4 d共576个数据作为网络训练样本,以第5 d(5月10日)的144个数据作为网络测试数据。
3.2 停车泊位时序相空间重构

(a);(b)
由图(b)可知,时间延迟系数==14。由式(2)可得,嵌入维数为5。用网络嵌入维数作为小波神经网络的输入节点数,可以有最佳的预测性能,因此小波神经网络网络输入层节点数为5,相应的隐含层节点数为2+1=11。设网络输入层时间序列为={()},将该单维的相空间拓展至多维的相 空间:

3.3 wolf法判定时序的混沌特性
利用前述wolf法步骤对本文的数据进行混沌特性判定,计算求得其Lyapunov最大指数为0.390 2,该指数大于0且小于1,验证了本文的停车泊位时间序列是具有混沌特性的,可将其重构至高维空间以映射出数据更多的隐含信息。
3.4 预测结果及分析评价
实验基于Matlab R2014a软件平台,用Matlab语言编写模型程序。遗传算法优化的小波神经网络模型相关参数设定如下:种群规模为40,最大遗传代数为200,代沟为0.9,小波神经网络学习速率为0.01,最大训练次数为500次。程序运行,得到遗传算法适应度曲线、小波神经网络训练误差收敛曲线如图5和图6所示。

图5 遗传算法适应度进化曲线

图6 小波神经网络训练误差曲线
为了证明本文采用方法的有效性和优越性,同时采用基于相空间重构的小波神经网络模型(CC- WNN)和未采用相空间重构的遗传算法优化小波神经网络模型(GA-WNN)对测试数据进行预测,同时,为验证WNN网络对小样本数据的适应性及优越性,引入CC-GA-BP模型,并将4种模型输出的预测结果与实际值进行对比分析。
由本文1.1节空余停车泊位波动率分析可知,全天06:00至09:00和17:00至19:00对应居民出行的早高峰和归来的晚高峰,空余停车泊位数波动较为剧烈,深夜时段停车泊位变动数较小,波动幅度小。因此本文截取时序数据中14:00至22:00的波动幅度较大的包含晚高峰的数据进行对比,4种模型第3次实验14:00至22:00的预测值与实际值拟合曲线如图6所示。

图7 各模型第3次实验的拟合曲线(14:00~22:00)
(14:00~22:00)
通过对比CC-GA-WNN模型与GA-WNN模型的预测结果曲线与实际值曲线的拟合程度,可以看出经过相空间重构的预测模型相比于未经重构的模型,其拟合程度较高,具有更好的预测效果。说明相空间重构合理地确定了小波神经网络的输入层个数,更好地挖掘了时序中蕴含的隐藏信息,从而得到了更好的预测结果。
通过对比CC-GA-WNN模型与CC-WNN模型的预测结果,采用GA算法优化过的预测模型的预测精度较高,与未经GA优化的预测模型相比,其与实际数据的拟合程度更高。说明采用GA算法有效提高了小波神经网络的稳定性,避免神经网络过早地陷入局部最小值,获取了神经网络更优的权值和阈值,表现出了更好的非线性拟合能力。
通过对比CC-GA-WNN模型与CC-GA-BP模型的预测结果,小波神经网络的网络结构是基于小波分析理论确定,避免了BP神经网络结构设计上的盲目性。从图7中各模型的预测效果可以看出,对于相同的预测任务,小波神经网络具有更强的学习能力,呈现出了更好的预测精度。
通过评价参数可以定量地评价预测模型的预测效果,计算各预测模型的评价参数进行对比分析。本文选取平均绝对误差()、最大绝对误差()、平均相对误差()及最大相对误差()4个评价参数对模型的预测效果进行评价,式(16)~(19)为评价指标的计算公式。
平均绝对误差:

最大绝对误差:
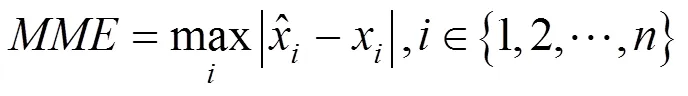
平均相对误差:
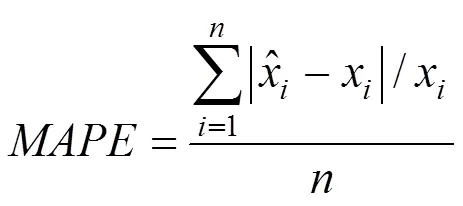
最大相对误差:
为了降低实验结果偶然性的影响,本文对4种模型分别进行3次预测实验,3次实验结果的评价指标平均值如表1所示,结果保留2位小数。
本文采用的CC-GA-WNN预测模型得到的预测结果平均绝对误差为3.83个,相比于CC-GA-BP,CC-WNN和GA-WNN模型,预测精度分别提高了2,3.35和5.25。同时平均相对误差、最大绝对误差、最大相对误差也均低于其他3种预测模型。说明通过对数据进行相空间重构,并结合遗传算法对参数进行优化,能有效降低预测误差,提高小波神经网络的预测精度。
综上可知,本文所提出的基于相空间重构和遗传小波神经网络的方法的预测结果与实际值具有较好的一致性,具备良好的应用价值。同时与其他3种模型相比,本文提出模型在各项评价指标中均表现最优,说明本文模型的优化方向是正确而有效的。
4 结论
1) 通过求解空余停车泊位时间序列的李雅普诺夫指数,证明该时间序列具有混沌特性,可通过相空间重构将其由一维序列扩展至多维序列,使其呈现出更多的隐含信息。
2) 提出了一种基于遗传小波神经网络的停车泊位预测方法,使用相空间重构技术对空余停车泊位时间序列进行重构,将重构后的序列作为小波神经网络的输入,同时使用遗传算法对小波神经网络的权值、阈值等参数进行优化,得到最终的预测 模型。
3) 以长沙市某居民区停车场为例,利用所提出的预测方法进行实验分析。结果表明:本文方法对空余停车泊位数量的预测具有较高精度;同时相比于单独使用未重构的小波神经网络模型、重构后未优化的小波神经网络模型、重构后优化的BP神经网络模型,其平均绝对误差、平均相对误差等指标均有较明显降低,说明该方法用于停车泊位短时预测场景中是有效的。
[1] 肖飞, 张利学, 晏克非. 基于泊位共享的停车需求预测[J] . 城市交通, 2009, 7(3): 73−79.XIAO Fei, ZHANG Lixue, YAN Kefei. Parking demand forecasting based on parking space sharing[J]. Urban Transport of China, 2009, 7(3): 73−79.
[2] 刘菲, 郝风杰, 郝敬全, 等. 基于优化LSTM模型的停车泊位预测算法[J]. 计算机应用, 2019, 39(增1): 65−69.LIU Fei, HAO Fengjie, HAO Jingquan, et al. Parking prediction algorithm based on optimized LSTM model[J]. Journal of Computer Applications, 2019, 39(Suppl 1): 65−69.
[3] 杜心. 基于LSTM神经网络的可用停车位预测模型研究[D]. 武汉: 武汉理工大学, 2018.DU Xin. Research on the prediction model of available parking space based on LSTM neural networks[D]. Wuhan: Wuhan University of Technology, 2018.
[4] GUO Jianhua, HUANG Wei, ZHU Xiaobo, et al. Real-time short-term forecasting method of remaining parking space in urban parking guidance systems[J]. Promet-Traffic & Transportation: Scientific Journal on Traffic and Transportation Research, 2018, 30(2): 173− 185.
[5] JI Yanjie, TANG Dounan, Blythe Phil, et al. Short-term forecasting of available parking space using wavelet neural network model[J]. IET Intelligent Transport Systems, 2015, 9(2): 202−209.
[6] JI Yanjie, GAO Liangpeng, CHEN Xiaoshi, et al. Strategies for multi-step-ahead available parking spaces forecasting based on wavelet transform[J]. Journal of Central South University, 2017, 24(6): 1503−1512.
[7] 陈群, 晏克非, 王仁涛, 等. 基于相空间重构及Elman网络的停车泊位数据预测[J]. 同济大学学报(自然科学版), 2007, 35(5): 607−611.CHEN Qun, YAN Kefei, WANG Rentao, et al. Parking space information prediction based on phrase construction and Elman neural network[J]. Journal of Tongji University (Natural Science), 2007, 35(5): 607− 611.
[8] 段满珍, 陈光, 张林, 等. 动态随机有效停车泊位预测方法[J]. 重庆交通大学学报(自然科学版), 2018, 37(6): 81−86.DUAN Manzhen, CHEN Guang, ZHANG Lin, et al. Prediction method of dynamic stochastic effective parking space[J]. Journal of Chongqing Jiaotong University (Natural Science), 2018, 37(6): 81−86.
[9] 张金梦, 刘慧君. 遗传算法优化BP神经网络的泊车位数量预测[J]. 重庆大学学报, 2018, 41(3): 76−81.ZHANG Jinmeng, LIU Huijun. Prediction of spare parking spaces based on BP neural network optimized by genetic algorithm[J]. Journal of Chongqing University, 2018, 41(3): 76−81.
[10] 陈海鹏, 图晓航, 王玉, 等. 基于小波-ELM神经网络的短期停车泊位预测[J]. 吉林大学学报(理学版), 2017, 55(2): 388−392.CHEN Haipeng, TU Xiaohang, WANG Yu, et al. Short-term parking space prediction based on wavelet- ELM neural networks[J]. Journal of Jilin University (Science Edition), 2017, 55(2): 388−392.
[11] 季彦婕, 陈晓实, 王炜, 等. 基于小波变换和粒子群小波神经网络组合模型的有效停车泊位短时预测[J]. 吉林大学学报(工学版), 2016, 46(2): 399−405.JI Yanjie, CHEN Xiaoshi, WANG Wei, et al. Short-term forecasting of parking space using particle swarm optimization-wavelet neural network model[J]. Journal of Jilin University (Engineering and Technology Edition), 2016, 46(2): 399−405.
[12] Kim H S, Eykholt R, Salas J D. Nonlinear dynamics, delay times and embedding windows[J]. Physica D, 1999, 127: 48−60.
[13] 杨飞. 基于回声状态网络的交通流预测模型及其相关研究[D]. 北京: 北京邮电大学, 2012.YANG Fei. Traffic flow prediction model based on echo state networks and related research[D]. Beijing: Beijing University of Posts and Telecommunications, 2012
[14] Rosenstein M T, Collins J J, De Luca C J. A practical method for calculating largest Lyapunov exponents from small data sets[J]. Physical D, 1993, 65(1): 117−134.
[15] Casetti L, Clementi C, Pettini M. Riemannian theory of Hamiltonian chaos and Lyapunov exponents[J]. Physical Review E, 1996, 54(6): 5969−5984.
>
Parking space prediction method based on genetic wavelet neural network
HAN Kun, LI Siyu
(School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China)
For parking space sharing mode, short-term and accurate prediction of the community parking space is beneficial for drivers to select a more suitable parking space, and is also conducive to the reasonable allocation of parking space resources. In this paper, a short-term prediction method for community parking spaces was proposed. Firstly, the phase space reconstruction of the free parking space time series is carried out by CC method and the predictability of the time series was proved by Lyapunov exponent method. Then the reconstructed time series was input into the wavelet neural network for training. The genetic algorithm was used to optimize the initial parameters of the wavelet neural network, and the optimum parameters were obtained after several iterations to establish the optimized prediction model. Finally, the algorithm is programmed by matlab, and the data of free parking spaces in a community in Changsha was investigated for experimental analysis. The results show that the CC-GA-WNN model has better prediction accuracy and optimization effect.
free parking space; phase space reconstruction; genetic algorithm; wavelet neural network
U491.7
A
1672 − 7029(2020)09 − 2216 − 09
10.19713/j.cnki.43−1423/u. T20191095
2019−12−06
国家级大学生创新创业训练计划资助项目(201610533302)
韩锟(1977−),女,湖北随州人,副教授,博士,从事载运工具智能测控与信息技术研究;E−mail:hkun@csu.edu.cn

(编辑 涂鹏)

