不规则型泊位与岸桥集成分配问题的优化建模和算法研究
赵 姣,胡 卉,袁华智
(1.长安大学运输工程学院,西安 710064;2.兰州理工大学土木工程学院,兰州 730050)
1 引 言
国际物流过程中集装箱港口的运营条件、服务质量、管理水平等均会影响到港口运输物流市场的竞争实力,而泊位和岸桥等港口资源的高效利用是提升各集装箱港口核心竞争力的主要因素.通常,针对每艘到港船舶均会有一个预设的离港时间,如果未能在预计离港时间之前完成船舶装卸任务,港口将缴纳滞期金.因此,如何通过泊位、岸桥等资源的合理分配,缩短船舶在港停泊时间,以及提高港口作业效率,进而为更多船舶提供高效、快捷的靠泊装卸服务是集装箱港口运营管理过程中重点关注的问题.
针对泊位分配和岸桥分配问题,已有学者开展了大量研究,并在提升集装箱港口作业效率方面取得了较大进展[1-5].在泊位分配问题研究方面,现有文献主要研究离散型和连续型泊位分配问题.离散型泊位分配问题是将泊位看作若干相互独立的泊位,且每个泊位在同一时间段内只能停靠一艘船,如图1所示.离散型泊位分配问题的研究方面,张新宇等[1]以总等待时间最少为目标,建立了考虑两艘船的离散泊位分配问题数学模型,设计了模拟退火多种群遗传算法进行求解.郑红星等[3]针对考虑潮汐影响的离散泊位分配问题进行了研究,并采用禁忌搜索算法进行求解.Bacalhau等[4]针对动态离散泊位分配问题进行研究,并针对此离散问题提出了一种混合遗传算法进行求解.泊位分配问题是提高港口运营效率的一个重要因素,与之相邻的岸桥优化问题则是确保快速装卸作业的另一个关键因素.因此,近年来,如何对有限的泊位、岸桥资源进行集成优化的问题受到国内外学者的广泛关注.Song等[5]针对离散泊位分配问题和岸桥调度问题进行了研究,其中所有的船舶都在调度计划开始前到达港口,每个泊位一次只能为一艘船服务,并为该问题提供一个多种方法集成的综合解决方案.

图1 离散型泊位分配问题
连续型泊位分配问题则是把泊位区看作连续的一段空间,船舶可在保持安全距离的情况下临近停泊,如图2所示.范志强[6]针对连续泊位分配问题进行了优化建模,并设计了遗传算法进行求解.王军等[7]采用动态学习方法对离散泊位分配方案进行了优化.Guo等[8]针对考虑天气情况下的连续泊位分配问题进行研究,并设计了粒子群算法进行求解.与离散泊位分配问题类似,连续型泊位和岸桥集成优化问题已吸引了众多学者的关注.Hendriks等[9]研究了一种联合运营的连续泊位分配问题,在该问题中,集装箱运营商为同一港口内的多个公司提供集装箱装卸物流服务,一个泊位可以服务多艘船.吴迪等[10]讨论了连续型泊位与岸桥集成分配问题,并设计了模拟植物生长交替进化算法进行求解.Wawrzyniak等[11]研究了连续型泊位和岸桥分配问题,并设计了启发式算法进行求解.Rodrigues等[12]针对连续型泊位和岸桥分配问题进行研究,设计了一种精确算法进行求解.

图2 连续型泊位分配问题
此外,在一些空间受限的集装箱港口(如比利时安特卫普港和新加坡港等),泊位线往往不呈一条直线,这些集装箱港口的泊位线,包含若干条直线,一条直线上包含多个泊位,即:同时包含离散和连续两种泊位分配情况,如图3所示.以往研究中对于空间受限的泊位分配问题研究较少.Imai等[13]最早针对锯齿型泊位分配问题进行了优化研究, 在此基础上,Imai等[14]考虑了由平行泊位线组成航道情况下的泊位分配问题.Correcher等[15]针对不规则布局的泊位分配问题进行研究,并设计了启发式算法进行求解.
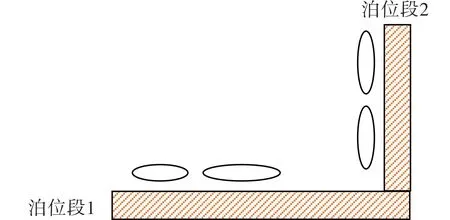
图3 不规则型泊位分配问题
针对不规则型泊位和岸桥分配问题的特点,将一条直线上的泊位定义为一个“泊位段”,每个泊位段有多个泊位和岸桥.当研究的港口只有一个泊位段,且每个泊位段内包含多个泊位时,则该问题为连续型泊位和岸桥分配问题;当研究的港口包含多个泊位段,且每个泊位段内只包含一个泊位时,则该问题为离散型泊位和岸桥分配问题.综上,离散和连续泊位和岸桥分配问题均可看作本文研究的不规则型泊位和岸桥分配问题的特殊情况.因此,已有的针对离散或连续型泊位和岸桥集成优化的方法,并不适用于不规则型泊位和岸桥分配问题.不管是直线型泊位或是不规则型泊位,当船舶在分配的泊位停泊后,均需由岸桥进行装卸作业,岸桥分配的数量直接影响船舶的装卸效率,因此有必要将不规则型泊位分配和岸桥分配进行集成优化.而现有的不规则型泊位分配问题的研究,很少同时考虑岸桥分配问题,且未对模型进行优化,导致建立的数学模型无法在短时间内获得最优解.为解决上述问题,本文首先建立了两种不规则型泊位和岸桥集成分配问题的数学模型,并对两种数学模型的求解效果进行了比较和分析;其次,提炼并加入了三个有效不等式,进一步改进了建立的数学模型;最后,设计了改进的粒子群算法对不规则型泊位和岸桥集成分配问题进行了求解,从而提高不规则型泊位类型港口的作业效率,降低运营成本.
2 问题描述与模型构建
2.1 问题描述
已知计划期内若干艘将入港船舶的长度、预计到港时间以及所需要的最大和最小岸桥数目,所有船舶必须在到港后开始停靠泊位并进行装卸作业.需决策每艘船的停靠泊位段,以及在该泊位段上的停泊位置、时间和岸桥,使得计划期内所有船舶在港停泊时间之和最小.某一不规则型泊位和岸桥分配结果如图4所示.每个矩形左下角的“数字”表示船号.每个矩形的左下角和左上角所在纵坐标的位置分别表示序号中对应船舶在分配到的泊位装(卸)货的开始时间和结束时间.同样,每个矩形的左下角和右下角对应的横坐标位置分别表示序号中对应船舶在分配到的泊位的起始位置和结束位置.在图4中,带虚线的矩形中的数字表示分配给每艘船的岸桥编号.
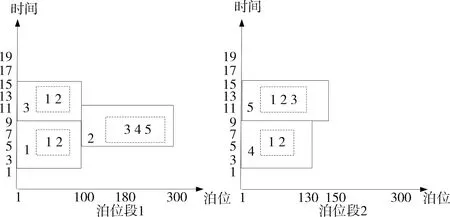
图4 不规则型泊位和岸桥分配方案
2.2 数学模型
考虑船舶之间的相对位置和服务时间,基于以下参数和决策变量建立不规则泊位和岸桥集成分配问题的数学模型.
已知参数如下,T为计划期内时间单位的集合,T={1,…,K},其中K是计划期间的时间单位总数;Ω为计划期内来港船舶的集合,Ω={1,…,N},其中N为计划期内来港船舶总数;Ψ为泊位段集合,Ψ={1,…,M},其中M是泊位段的总数;Qj为泊位段j的岸桥数;Pijc为船i在泊位段j上分配c台岸桥时的卸载时间;li为船i的长度;Lj泊位段j的长度;εi为可用于i船的港口岸桥的最大数量;θi为可用于i船的港口岸桥的最小数量;ri为船i的到达时间.
建立不规则型泊位和岸桥集成分配问题的数学模型:
(1)
∀i∈Ω,i′∈Ω{i},j∈Ψ
(2)
∀i∈Ω,i′∈Ω{i},j∈Ψ
(3)
∀i∈Ω,i′∈Ω{i},j∈Ψ
(4)
∀i∈Ω,i′∈Ω{i},j∈Ψ
(5)
∀i∈Ω,i′∈Ω{i},j∈Ψ
(6)
(7)
∀i∈Ω,j∈Ψ
(8)
(9)
(10)
(11)
(12)
(13)
Di≤K∀,i∈Ω
(14)
∀i∈Ω,i′∈Ω{i},j∈Ψ
(15)
∀i∈Ω,j∈Ψ
(16)
2.3 有效不等式
为进一步提高2.2部分不规则型泊位和岸桥集成分配问题数学模型的求解效果,结合问题特性和变量关系,提炼出该模型的三个有效不等式如下.
(17)
(18)
(19)
3 算法设计
粒子群算法是由Eberhart等[16]提出的一种基于种群的智能优化算法.由于其收敛快速以及需要设置的参数较少等特点,粒子群算法已经得到了广泛的应用[17-19].在粒子群算法中,种群由若干粒子组成,且每个粒子在每次迭代中都有一个位置和速度向量,位置决定解的质量,而速度决定粒子在下一代的移动方向.粒子的速度和位置更新公式如下.
(20)
(21)
(22)

3.1 解的表示和初始解的生成
由于离散和连续泊位和岸桥分配问题均可看作本文研究的不规则型泊位和岸桥分配问题的特殊情况,即:当研究的港口只有一个泊位段,且每个泊位段内包含多个泊位时,则该问题为连续型泊位和岸桥分配问题;当研究的港口包含多个泊位段,且每个泊位段内只包含一个泊位时,则该问题为离散型泊位和岸桥分配问题.因此,不同于离散型泊位和岸桥分配问题的粒子群算法,针对不规则泊位和岸桥分配问题进行研究,同一时段内,每个泊位段不只停留一艘船,而是可以停留多艘船,在粒子群算法解码过程中,不仅需要决策船舶的停靠泊位,还需要决策船舶在分配的泊位段上的具体停泊位置;不同于连续型泊位和岸桥分配问题的粒子群算法,针对不规则泊位和岸桥分配问题进行研究,不仅包含一个泊位段,而是每个泊位段均需决策哪些船舶在该泊位段上停泊,以及具体的停泊位置.即:不规则型泊位和岸桥集成调度问题需要决策每艘船停靠的泊位段,以及在该泊位段上的停泊位置、停泊时间和分配的岸桥号.首先采用粒子群算法进行泊位段的分配和岸桥数目的分配,然后再设计启发式对船舶的停泊位置和停泊时间进行分配,从而得到不规则型泊位和岸桥集成分配问题的优化方案.
定义1N=|Ω|,代表需要停靠的船舶数目,用一个2N维的序列表示一个解.其中第一个N维代表为相应的船舶分配的泊位段的编号,每一维的值都是0到M之间的一个实数值.第k维的值Xk表示船舶i被分配给泊位段⌈Xi⌉停泊并进行装卸作业.第二个N维代表每艘船被分配的岸桥数目,每一维的值都是0到q′=min(εi,Qj)之间的一个实数值,其中Qj为泊位段j上的岸桥数量,εi为船舶i的最大服务岸桥数量.第N+k维的值Xk+N表示船舶i在对应的泊位段上被分配的岸桥数量.图5中为3个泊位段,每个泊位段有3台岸桥,到港5艘船的粒子群算法初始解.第一个N维代表为每艘船舶分配的泊位段的编号,将图中前5个随机生成的实数向上取整,得到1~5号船舶的停靠泊位段分别为1,3,2,2,1;第二个N维代表每艘船被分配的岸桥数目,将图中后5个随机生成的实数向上取整,得到1~5号船舶的分配的岸桥数量分别为1,3,2,3,2.分配每艘船舶所在的泊位段后,将每个泊位段上的船舶按照到达时间从小到大进行排序,依次计算每艘船的停泊位置和停泊时间,以及分配的岸桥.每一艘船舶分配停泊位置和岸桥后,计算该泊位段当前剩余空闲长度和空闲岸桥数量,当剩余泊位段长度不满足下一艘船的长度要求,或者剩余岸桥数目少于下一艘船所需要的最小岸桥数目时,计算当前占用该泊位段的所有船舶服务结束时间,当占用该泊位段的所有船舶服务结束后,下一艘船开始接受服务.

图5 粒子编码和解码示意图
采用随机的方式产生初始解以保证解的多样性.每一个粒子的第一个N维在0到M之间随机产生,第二个N维在0到Qj之间随机产生.
3.2 适值计算及算法终止条件
适应度值根据原始目标函数值计算,一个粒子对应的适应度值为:计划期内所有到港船舶在港停泊时间之和.
判断当前迭代次数是否达到最大迭代次数(Max_iteration),若是,停止迭代,选择适应度值最小的粒子所对应的解作为不规则型泊位和岸桥集成分配问题的优化解输出;否则,继续进行迭代,直到达到最大迭代代数为止.
3.3 粒子群求解过程
基于上述描述,下面给出粒子群算法求解不规则型泊位和岸桥集成分配问题的过程.
步骤1:初始化种群中的所有粒子,得到泊位和岸桥分配方案.迭代次数设为1.
步骤2:对于每一个粒子,根据分配的泊位段和岸桥数目,计算每艘船所在泊位段的停泊位置、停泊时间以及服务岸桥号.
步骤3:计算每个粒子的适应度值.
步骤4:更新每个粒子的最好位置值以及种群的最好位置值.
步骤5:根据式(22)和式(21)更新每一个粒子的速度和位置值.
步骤6:如果达到最大迭代次数,算法停止;否则,转到步骤2.
4 计算实验
4.1 算例产生
采用CPLEX 12.5软件求解不规则型泊位和岸桥集成分配问题的最优解,但对船舶数较多问题的求解时,CPLEX12.5无法在1 h内获得问题的可行解,因此采用C++编码的PSO算法,所有实验在一台cpu 3.2 GHz,4 GB内存的计算机上进行.结合港口实际情况和文献[20]的数据,设定每个泊位段长度为300 m,岸桥数目为5台,到港船舶的长度在li=U[80, 300],i=1,2,…,N.每艘船舶的到港时间和一台岸桥的服务时间分别服从[1, 100]和[10, 60]的均匀分布.服务每艘船舶的最大和最小岸桥数目为εi=li/50,θi=1+0.3εi.将每个泊位段均看作50 m为1个单位长度,同时将船舶也看作50 m为1个单位长度,将实际泊位段和船舶长度转换为若干单位长度,从而针对不规则型泊位和岸桥集成分配问题进行求解,最后将求解到的结果再乘以50转化为泊位段和船舶的实际长度,既加快了CPLEX的求解时间,同时也基本不影响原问题的优化结果.
4.2 计算结果
采用CPLEX软件求解泊位段为2,船舶数为5的8个算例,针对原模型(记为M)和加入有效不等式后的模型(记为M′)的求解结果如表1所示,其中,Gap =(模型M求解时间-模型M′求解时间)×100%/模型M求解时间.针对加入有效不等式前后的模型进行求解均获得了最优解,从表2可以看出,加入有效不等式后,模型的平均求解时间减少了83.39%.

表1 加入有效不等式前后CPLEX求解模型M的结果对比
以船舶数目为8的算例为例,该算例中的已知数据见表2,不规则型泊位和岸桥集成分配的优化方案如图6所示.船舶3,4和6被分配到泊位段1;船舶2和5被分配到泊位段2;船舶1,7和8被分到泊位段3.在泊位段1中,船舶6最先到达,岸桥1和2为其进行装卸作业,开始和结束时间分别为2和19,停泊位置从1到150;岸桥1为船舶3进行装卸作业,开始和结束时间分别为22和31,停泊位置从51到150;岸桥3和4为船舶4进行装卸作业,开始和结束时间分别为12和31,停泊位置从151到300.

图6 不规则型泊位和岸桥分配方案

表2 船舶数为8的算例已知参数
表3和表4为不同迭代代数和随机学习因子参数设置下的求解结果,可以看出当迭代代数为1000代,学习因子c3取1.5时,PSO算法的求解结果更优,因此,将迭代代数设置为1000代,随机学习因子设置为1.5.
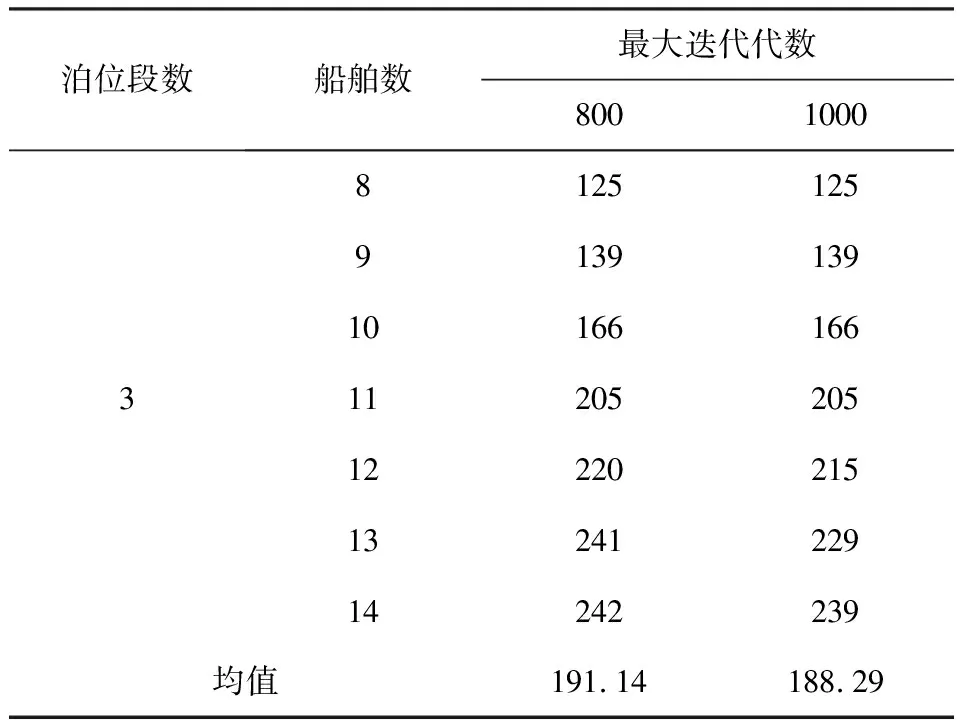
表3 改进PSO算法不同迭代次数的结果

表4 改进PSO随机学习因子参数设置
表5为标准粒子群算法、改进粒子群算法以及CPLEX求解结果的对比,偏差1=(SPSO-IPSO)×100%/IPSO;偏差2=(IPSO-CPLEX)×100%/CPLEX.从实验结果可以看出,改进前后粒子群算法求解结果偏差的最大值为25.52,在所有实验中,偏差的平均值为16.62.随着船舶数量的增加,偏差呈现逐渐增大的趋势.改进粒子群算法的求解结果与CPLEX算法求解结果的最大偏差为4.37%,平均偏差为2.89%,而CPLEX软件的平均求解时间为253.77,改进粒子群算法的平均求解时间仅为0.39 s,证明了设计的粒子群算法的有效性.

表5 标准PSO、改进PSO和CPLEX结果对比
为了验证本文改进粒子群算法在求解较大规模问题时的有效性,分别采用标准PSO和改进PSO对不同规模的问题进行求解,结果如表6所示,表中偏差 =(SPSO-IPSO)×100%/IPSO,每个规模的结果均为10组同规模算例求解所得的平均值.可以看到,在各个规模下,改进PSO的结果均优于标准PSO的结果,证明了改进PSO在求解较大规模问题时的有效性.

表6 标准PSO和改进PSO结果对比
综上,在模型中加入有效不等式后,模型的求解时间明显减少.在所有算例中,改进粒子群算法的求解结果均优于标准粒子群算法的求解结果,这是由于标准粒子群算法容易陷入局部最优,加入随机学习因子后,增加了粒子寻优的范围,更容易找到优化解.从表5和表6可以看出,改进粒子群算法相比标准粒子群算法,在求解质量上分别提高了16.62%和33.80%,即:针对全部17个算例,求解质量平均提高了25.21%.
5 结 论
本文研究了集装箱港口不规则型泊位和岸桥集成分配问题.针对该问题,我们建立了线性规划数学模型,并通过CPLEX软件进行求解;针对问题规模增加,求解时间变长的问题,在模型中加入三个有效不等式,使模型的求解时间降低了83.23%.针对船舶数目增加后,CPLEX软件无法在可接受时间内求解的情况,本文提出了粒子群算法进行求解.实验结果证明,改进粒子群算法相比标准粒子群算法,求解质量提高了25.21%,证明了本文设计的改进粒子群算法在求解不规则型泊位和岸桥分配问题时的有效性.
本文的研究为针对计划期内所有船舶到港时间不再发生变化的情况,且只考虑了岸桥进行贝位作业的分配,未考虑岸桥进行对应贝位装卸作业的先后顺序安排,未来将针对船舶到达时间不确定的不规则泊位和岸桥集成调度问题进行建模和优化研究.

