车轮扁疤对高速车辆动态曲线通过性能的影响
王相平,王红兵,贾文慧,李国芳,丁旺才
车轮扁疤对高速车辆动态曲线通过性能的影响
王相平,王红兵,贾文慧,李国芳,丁旺才
(兰州交通大学 机电工程学院,甘肃 兰州 730070)
为探究车轮扁疤对高速车辆动态曲线通过的影响,建立基于轮对柔性的车辆−轨道刚柔耦合模型,推导新、旧扁疤长度与深度之间的关系,在考虑轮轴弹性变形的基础上分析不同曲线超高下扁疤尺寸变化对曲线通过的影响规律。研究结果表明:转向架二位轮对内轨侧车轮出现扁疤对车辆曲线通过影响最大;新扁疤尺寸越大越不利于曲线通过;旧扁疤沿深度扩展对曲线通过的影响大于沿长度扩展的影响;内轨侧车轮在欠超高时轮轨磨耗、脱轨系数和轮轨横向力更大,过超高时倾覆系数、轮轨垂向力较大;扁疤对车辆曲线通过的影响主要体现在对曲线线路结构的破坏上,建议在充分考虑轮轨型面的基础上以轮轨垂向力峰值为标准确立扁疤车轮镟修界限。
高速车辆;车轮扁疤;曲线通过;刚柔耦合;动力学
车轮扁疤是车轮材质过软、加工工艺不良、同一轮对轮径差过大或紧急制动、轮对空转等造成的车轮踏面擦伤和剥离的统称,是一种常见的轮对踏面缺陷。当车辆高速通过曲线线路时,线路变化对轮轨动力响应会产生严重影响,车轮扁疤在轮轨接触面间也会产生间歇性脉冲激扰(扁疤效应),影响轮轨接触性能,严重时甚至威胁车辆运行安全。凌亮等[1]采用轮心轨迹函数描述车轮扁疤,研究表明300 km/h速度下扁疤冲击产生的轮轨法向力为静载时的3~8倍;杨光等[2]基于轮径变化模拟扁疤,研究显示扁疤对轮轨系统垂向冲击作用较为显著;REN[3]建立三维扁疤模型,研究了高速车辆−轨道系统三维扁疤冲击下的轮轨振动特征;BIAN等[4]建立包含扁疤的轮轨系统有限元模型,研究表明扁疤冲击力随扁疤尺寸增大而增大;Marijonas等[5]研究表明扁疤冲击力大小取决于扁疤尺寸、车轮直径和车速。以上研究从扁疤尺寸变化方面深入分析了车辆通过直线线路时的轮轨动力响应,并从车辆运行安全性、轨道结构动力响应等方面给出了扁疤长度限值。然而列车高速通过曲线线路时轮轨动态作用更加剧烈。刘鹏飞等[6]对欠超高状态下车辆曲线通过时的轮重增减载和悬挂系统承载特性进行了研究;WANG等[7]探究了列车高速通过曲线线路时的导向机理及动力学性能。根据以上研究不难发现,有关曲线通过的研究目前主要集中在线路参数选择、轮轨匹配及磨耗方面,踏面缺陷对曲线通过影响方面的研究相对较少,尤其是扁疤效应对曲线通过影响方面的研究几乎没有。车轮扁疤作为一种常见的踏面缺陷,对轮轨接触产生巨大影响。曲线线路作为高速铁路线路的薄弱环节,当存在扁疤车轮的列车高速通过曲线线路时,扁疤与线路曲率变化的共同作用会导致轮轨动态作用加剧,破坏线路结构,影响列车运行安全。鉴于此,本文建立基于轮对柔性的车辆−轨道刚柔耦合模型,在考虑轮轴弹性变形的基础上分析不同超高下扁疤冲击对高速车辆曲线通过性能的影响,探索扁疤扩展对车辆运行安全性、平稳性、轨道结构动力响应和轮轨磨耗的影响,研究结论为轮对镟修、线路养护维修提供理论参考和指导。
1 计算分析模型
1.1 基于轮对柔性的车辆-轨道耦合模型
列车运营中,轮对因受到轴箱传递的压力和钢轨的支撑作用而发生轮轴弯曲变形;车辆在曲线线路运行时,由于曲线超高作用内外轨受载不均也会导致轮轴弯曲变形,轮轴弯曲变形使轮轨接触斑公法线与轮对滚动轴线不垂直,从而产生自旋效应。Baeza等[8]在考虑轮对绕轴线旋转的基础上分析了带扁疤的柔性轮对对车辆−轨道动力学性能的影响;WU等[9]对比研究带有扁疤的刚性和柔性轮对的车辆−轨道动力响应,发现柔性轮对能显著提高轮轴应力;杨光等[10−11]也对柔性轮对的动力学性能进行了探究,相关研究结果表明,使用柔性轮对能充分体现轮轴弯曲引起的轮对旋转效应。
车辆在曲线线路运行时,动力学性能受线路曲率变化影响较大,多刚体模型并未考虑轮轴弹性变形,因此计算得到的相关评价指标普遍偏大[10−12],不能准确反映高速列车曲线通过时的动力学性能变化,故需将轮对柔性化处理。轮对柔性化处理指对轮对模态分析并通过模态缩减生成柔性轮对[10−11]。轮对有限元模型如图1所示。车轮名义滚动圆直径920 mm,直腹板厚30 mm,空心车轴。轮对采用Solid185三维实体单元,用体扫掠法划分网格,最小网格尺寸2 mm,在确保计算精度满足要求、计算量尽可能小的前提下保证节点与扁疤离散点尽可能多的对应。网格划分后共有217 911个节点,201 062个单元。计算轮对自由模态,去除前6阶刚体模态,轮对7~20阶弹性模态中,第12,15~19阶振型为车轮弯曲或横向拉伸变形,其余阶次振型为车轴扭转或弯曲变形。

图1 轮对有限元模型
采用文献[2]使用的子结构法对轮对有限元模型进行处理,生成柔性轮对。然后去除多刚体模型中需要柔性化处理的轮对部分,将柔性轮对模型与其余多刚体模型组装,生成基于轮对柔性的车辆刚柔耦合系统。其中,柔性轮对通过旋转铰与轴箱连接,实现轮对旋转运动。
车速300 km/h时车轮滚过40 mm扁疤的时间仅为48 ms,可见扁疤冲击力作用极快,直接由钢轨承受,因此对轨下结构做进一步简化,仅考虑钢轨和扣件作用[13]。车辆−轨道耦合系统中,钢轨采用移动质量轨道[12],轨道不平顺UIC-good。车轮踏面LMA,钢轨类型60N,轮轨接触模型Kik- Piotrowski。Kik-Piotrowski是一种基于虚拟渗透的接触理论,考虑轮对摇头的虚拟渗透函数为[14]


1.2 车轮踏面扁疤模型
从产生机理看,扁疤可看作踏面某位置切割出的弦线;从作用效果看,扁疤效应主要体现为对轨道的垂向冲击1−5]。因此研究扁疤垂向作用时可不必考虑扁疤宽度变化[13]。
采用离散点法建立沿p处滚动圆圆周对称的扁疤模型,通过对车轮踏面指定位置廓形的改变来模拟扁疤。模拟方法如图2所示。
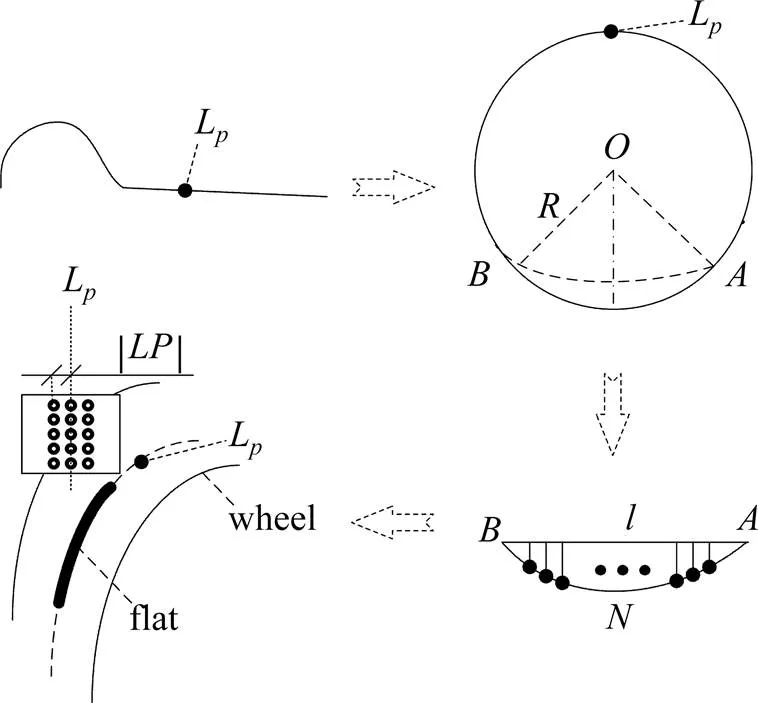
图2 扁疤模拟方法
总体技术路线如下:
1) 在车轮踏面上确定扁疤作用位置L及其与车轮名义滚动圆圆周横向跨距||;
2) 通过L处滚动圆半径及其与扁疤长度、深度之间的关系,确定扁疤参数;

4) 结合车轮廓形,根据坐标将这些离散的点沿车轮圆周方向布置,生成车轮扁疤。
其中,为弧沿直线方向等分的份数。为便于表示离散点的坐标,将取为定值。=37,取恒定宽度w=2||= 6 mm。
扁疤几何模型如图3所示。

图3 车轮扁疤几何模型
由图3得新扁疤长度0与深度关系为

对旧扁疤,假定两侧棱角磨圆部分形状对称,采用三次抛物线()模拟其棱角被磨圆部分。以轮心为原点,竖直向上为轴建立平面直角坐标系,求得离散点纵坐标

旧扁疤几何关系

新、旧扁疤之间关系

现场检测表明扁疤通常出现在车轮名义滚动圆圆周附近[13],故取L=0,对应扁疤的主要参数见表1。

表1 旧扁疤尺寸范围
1.3 模型验证
车辆−轨道耦合动力学模型中,轮轨法向力 为[13]

式中:,为轮轨材料的弹性模量和泊松比。为轮轨接触点上的弹性位移。

为模态阶数;h为对应振型函数;w为模态坐标。
刚性轮对未考虑车辆运行过程中轮轨接触点瞬时弹性位移,故=0,柔性轮对>0;由式(7)~(8)知,增大时会减小,即柔性轮对模型轮轨法向力略小于多刚体模型。
以自旋蠕滑率验证轮对旋转效应。车轮自旋蠕滑率为
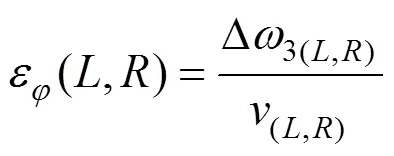
式中:(L,R)为车轮名义前进速度;为旋转速度。

式中:φ为摇头角;0为车轮名义滚动圆半径;(L,R)为左右轮实际滚动圆半径。
柔性轮对轮轨接触点上会产生微小弹性位移,故车轮实际滚动圆半径略小于刚性轮对。由式(9)知,(L,R)减小会导致ε(,)增大。因此在曲线线路上,柔性轮对自旋蠕滑率应大于刚性轮对。
采用同参数的多刚体模型和考虑轮对柔性的刚柔耦合模型通过同参数的曲线线路时,二位轮对内轨侧车轮轮轨法向力及自旋蠕滑率如图4所示。

图4 模型对比
由图4知,使用多刚体模型得到的轮轨法向力大于刚柔耦合模型,通过刚柔耦合模型计算的车轮自旋蠕滑率大于多刚体模型。这与上述理论推导结果一致,说明考虑轮对柔性的车辆−轨道系统模型是满足计算需求的,且能体现轮轴弯曲变形引起的旋转效应。
为进一步说明模拟结果的准确性,将本文模型计算结果与文献[3]进行对比,对比结果见表2。表2中,轮轨垂向力为1(一位轮对右侧车轮)车轮有扁疤时,车辆通过无激扰直线线路时的计算结果。

表2 计算结果对比
由表2知,本文模型计算结果与文献[3]计算结果基本接近。由于扁疤模拟方法、尺寸参数略有差异,所以计算结果存在微小不同是合理的。同时这一结果也说明所建模型能够准确模拟扁疤结构。
2 扁疤作用下车辆曲线通过性能分析
2.1 曲线线路参数及性能评价指标
选取曲线半径=7 000 m,理论超高

式中:为曲线半径,m;为列车运行速度,km/h。车速300 km/h时,超高150 mm,参考《高速铁路设计规范》[15],选取曲线线路参数见表3。动力性能评价指标见表4[16]。

表3 曲线线路参数

表4 动力性能评价指标
2.2 车轮扁疤分布与车辆动力响应关系分析
为全面考量扁疤对车辆动态曲线通过的影响,按照车辆前转向架一、二位轮对左右车轮同一位置分别出现扁疤的情况,探讨同一转向架不同车轮出现扁疤时轮轨响应关系。
轮轨垂向力反映了扁疤对轨道的冲击作用,是扁疤对车轮的直接作用;倾覆系数表示车辆在各种不利因素下是否会发生倾覆,是扁疤对整车性能的间接影响。因此选取轮轨垂向力和倾覆系数来衡量扁疤对车辆动力学性能的影响效果。理论超高下带有长35 mm深0.10 mm扁疤的车辆以300 km/h通过无激扰右曲线线路,圆曲线上轮轨垂向力、脱轨系数变化如图5和图6所示。

图5 轮轨垂向力变化曲线

图6 倾覆系数变化曲线
由图5~6知,无扁疤车轮的轮轨垂向力、倾覆系数为一条直线,有扁疤时会出现间歇性脉冲激扰。不同车轮同一时刻轮轨垂向力、倾覆系数并非同步变化,而是出现了一定的超前或滞后,这是因为车辆曲线通过时轮对摇头运动导致轮轨接触点不在车轮主廓线上。接触点存在一定的超前或滞后是相关指标出现超前或滞后的根本原因。同时,图5~6表明,2有扁疤时轮轨垂向力、倾覆系数变化最大,因此选取2为研究对象,探究扁疤扩展对车辆动态曲线通过的影响。
2.3 扁疤扩展对车辆动态曲线通过的影响
2.3.1 新扁疤对车辆动态曲线通过的影响
新扁疤长度与深度之间对应关系如式(4)所示。取新扁疤深度=0.10~0.50 mm,对应扁疤长度见表5。

表5 新扁疤尺寸
理论超高下,车辆运行安全性、轨道结构动力响应指标如图7和图8所示。

图7 新扁疤下车辆运行安全性

图8 轨道结构动力响应
由图7知,扁疤尺寸越大,倾覆系数越大,脱轨系数先增大后减小。由图8知,扁疤尺寸增大,轮轨垂向力显著增大,轮轨横向力、轮轴横向力也相应增大,但>0.3 mm时轮轴横向力增大趋势不及轮轨横向力。
图9为不同扁疤对应构架Sperling指数。
由图9知,扁疤尺寸增大,垂向Sperling指数在±0.10范围内波动,横向Sperling指数并未发生明显变化。这是因为扁疤冲击直接作用在垂向,故对横向Sperling指数不会有较大影响,而高速旋转轮对上扁疤引起的垂向振动会引起轴箱、构架振动[9],从而导致构架垂向Sperling指数发生波动。

图9 新扁疤下车辆运行平稳性
轮缘摩擦功表示轮缘磨耗的快慢

式中:为摩擦因数;为法向力;为摩擦速度。
磨耗指数用于衡量轮轨磨耗程度,磨耗指数越大则车轮磨耗越严重。计算公式为

式中:F,F和F表示纵向、横向和自旋蠕滑力;,和表示纵向、横向和自旋蠕滑率。
轮轨磨耗指标如图10所示。由图10知,扁疤深度<0.4 mm时,深度越大磨耗指数和摩擦功也越大,但当扁疤深度在0.4 mm和0.5 mm时磨耗指数和摩擦功略有减小。

图10 新扁疤下轮轨磨耗
2.3.2 旧扁疤对车辆动态曲线通过的影响
新扁疤演变为旧扁疤时,两侧棱角会被磨圆,因此可认为是扁疤深度不变沿长度方向的扩展,但对一些长度较长的新扁疤,其扩展可认为是长度不变沿深度的变化。因此,分别从扁疤长度不变深度改变和深度不变长度改变2个方面来探究扁疤扩展对高速车辆动态曲线通过的影响。
扁疤沿深度、长度扩展时车辆运行安全性指标如图11和图12所示。

图11 车辆运行安全性(d)

图12 车辆运行安全性(l)
由图11~12知,扁疤沿深度或长度扩展都会导致倾覆系数和脱轨系数增大。超高越大,倾覆系数、内轨侧车轮脱轨系数幅值也越大。当扁疤深度<0.3 mm时,扁疤深度的增大导致脱轨系数和倾覆系数变化量较大,当>0.3 mm时增长趋势减缓;而扁疤沿长度扩展时,在=60 mm前后增长速度也有明显变化,这是因为旧扁疤深度为0.3 mm时对应的长度在60 mm左右。
扁疤沿深度、长度扩展时轨道结构动力响应如图13和图14所示。

图13 轨道结构动力响应(d)

图14 轨道结构动力响应(l)
由图13~14知,扁疤沿长度和深度扩展导致轮轨垂向力有不同程度增大,扁疤沿深度扩展时轮轨横向力增大,扁疤沿长度扩展时轮轨横向力反而减小。这是因为扁疤深度不变长度增大时,扁疤在车轮踏面上造成的损伤越接近车轮主廓线,轨道与扁疤区域接触面积增大,从而导致轮轨横向力减小。对比图13~14知,曲线超高越大,内轨侧轮轨垂向力越大,轮轨横向力越小。
扁疤沿深度或长度扩展时轮轨磨耗指标如图15~16所示。由图15~16知,扁疤沿深度或长度扩展都会加重轮轨磨耗,但扁疤沿深度扩展时轮轨磨耗程度显著大于沿长度扩展时的轮轨磨耗。这是因为当扁疤长度不变深度增大时,扁疤在车轮踏面上造成的缺陷越大,故车辆驶过缺陷区域周围时轮轨磨耗程度也越大。

图15 轮轨磨耗指标(d)

图16 轮轨磨耗指标(l)
图15~16显示,扁疤沿深度扩展时理论超高下的摩擦功、磨耗指数小于过超高和欠超高情况。这是因为理论超高能够很好的平衡车辆曲线通过时的离心力,故车辆整体动力学性能指标要优于过超高和欠超高工况。
扁疤沿长度和深度扩展时车辆运行平稳性指标如图17~18所示。由图可知,扁疤沿深度或长度扩展都不会影响车体平稳性,这是因为扁疤本身几何尺寸较小,其产生的振动冲击也不会很大,经两系悬挂装置缓冲减振后对车体几乎无影响。对比不同超高下车体的Sperling指数,可发现理论超高下垂向和横向Sperling指数远小于过超高和欠超高情况。过超高时垂向Sperling指数大于欠超高,横向Sperling指数几乎无差别。

图17 平稳性指标(d)

图18 平稳性指标(l)
3 车轮扁疤安全限值
从前文分析知,随着扁疤尺寸增大,轮轨垂向力逐渐超出安全值。因此可见,扁疤对车辆曲线通过的影响主要体现在对轨道结构的破坏上。同时,我国《高速铁路设计规范》指出轨道承载能力主要由扁疤冲击力核算[15]。故应以轮轨垂向力为标准确定曲线线路上的扁疤限值。
基于Hertz接触理论的轮轨垂向力为
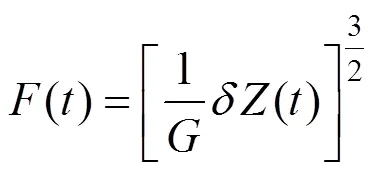
式中:为与踏面廓形有关的轮轨接触常数;()为轮轨间弹性压缩量。由式(14)可知,轮轨垂向力与轮轨间的弹性变形及踏面形式有关;由式(7)知垂向力与轮对材料、尺寸有关。因此,在考虑扁疤车轮镟修界限时还应充分考虑轮对型号和踏面形式。
不同型号的车轮对应于不同的轮重和轮径。考虑轮重的扁疤冲击力可表示为[13]


式中:1和2为一系簧上、簧下质量;为扁疤长度;为车轮旋转惯量转换为往复惯量的系数;为车辆运行速度。由式(15)~(16)知,轮对质量越大,扁疤车轮冲击力也越大。式(3)表明,同一扁疤深度,轮径越大扁疤长度越大,而扁疤深度不变长度增大时(<74 mm),冲击力也对应增大。也就是说,同一深度扁疤,轮对参数越大扁疤冲击力也越大[5]。扁疤限值的设置是为了找到轮轨垂向力峰值(170 kN)所对应的扁疤几何尺寸最大值。因此,选取轮径920 mm的PW-200轮对进行限值分析。因为,能够满足大尺寸轮对扁疤车轮镟修的扁疤深度限值理论上是完全满足小尺寸轮对的,而与之对应的长度限值可通过式(3)~(5)计算得出。
鉴于我国铁路主要以高速或提速运营为主,固选取国内高速动车组常用的具有典型代表意义的LMA型和S1002CN型踏面进行限值研究。以CRH3型车300 km/h通过某半径7 000 m曲线线路为例,线路参数见表3,不同踏面形式与60轨匹配时扁疤扩展对应轮轨垂向力峰值等高线图如图19所示。

(a) S1002CN-60 N轮轨垂向力;(b) LMA-60 N轮轨垂向力
我国标准规定,车轮作用于轨道的垂向力不超过170 kN[16]。据此,根据图19分析结果结合式(3)~(5)计算出不同型号轮对扁疤限值见表6。
不同踏面类型导致轮轨接触关系产生差异,引起轮轨垂向力变化,对扁疤限值产生影响。故制定扁疤限值时应在充分考虑轮轨型面的基础上以轮轨垂向力为评判标准。
4 结论
1) 扁疤车轮通过曲线线路时,不同车轮的动力响应差别较大。内轨侧车轮出现扁疤对车辆曲线通过的影响远大于外轨侧;转向架二位轮对内轨侧车轮出现扁疤对车辆曲线通过性能影响最大。
2) 新扁疤尺寸越大越不利于曲线通过;旧扁疤沿深度方向扩展对曲线通过的影响远大于沿长度方向扩展的影响。扁疤车轮通过欠超高线路时轮轨磨耗、脱轨系数和轮轨横向力大于理论超高及过超高的情况;扁疤车轮通过过超高线路时倾覆系数、轮轨垂向力和车辆运行平稳性指标显著大于理论超高和欠超高状态。
3) 扁疤尺寸的增大会对构架垂向振动产生影响,但不会影响到车体平稳性。扁疤对车辆曲线通过的影响主要体现在对线路结构的破坏上,确立扁疤限值时应在充分考虑轮轨型面的基础上以轮轨垂向力为评判标准。
[1] 凌亮, 曹亚博, 肖新标, 等. 车轮擦伤对高速轮轨接触行为的影响[J]. 铁道学报, 2015, 37(7): 32−39. LING Liang, CAO Yabo, XIAO Xinbiao, et al. Effect of wheel flats on the high-speed wheel-rail contact behavior[J]. Journal of the China Railway Society, 2015, 37(7): 32−39.
[2] 杨光, 任尊松, 袁雨青. 车轮扁疤伤损对高速列车轮对动力学性能影响[J]. 北京交通大学学报, 2018, 42(3): 103−111. YANG Guang, REN Zunsong, YUAN Yuqing. Influence of wheel flat on dynamic performance of high-speed train wheelset[J]. Journal of Beijing Jiaotong University, 2018, 42(3): 103−111.
[3] REN Zunsong. An investigation on wheel/rail impact dynamics with a three-dimensional flat model[J]. Vehicle System Dynamics, 2019, 57(3): 369−388.
[4] BIAN Jian, GU Yuantong, Murray, et al. A dynamic wheel-rail impact analysis of railway track under wheel flat by finite element analysis[J]. Vehicle System Dynamics, 2013, 51(6): 784−797.
[5] Marijonas Bogdevicius, Rasa Z, Bureika, et al. An analytical mathematical method for calculation of the dynamic wheel-rail impact force caused by wheel flat[J]. Vehicle System Dynamics, 2016, 54(5): 689−705.
[6] 刘鹏飞, 翟婉明, 王开云, 等. 机车车辆通过缓和曲线时悬挂系统及轮重的动态特性[J]. 中国铁道科学, 2013, 34(1): 67−74. LIU Pengfei, ZHAI Wanming, WANG Kaiyun, et al. The dynamic characteristics of suspension system and wheel load for rolling stock passing through transition curve[J]. China Railway Science, 2013, 34(1): 67−74.
[7] WANG KY, HUANG C,ZHAI W M, et al. Progress on wheel-rail dynamic performance of railway curve negotiation[J]. Journal of Traffic and Transportation Engineering (English Edition), 2014, 1(3): 209−220.
[8] Baeza L, Fayos J, Roda A, et al. High frequency railway vehicle-track dynamics through flexible rotating wheelsets [J]. Vehicle System Dynamics, 2008, 46(7): 647−659.
[9] WU X W, Rakheja Subhash, Ahmed A K W, et al. Influence of a flexible wheelset on the dynamic responses of a high-speed railway car due to a wheel flat[J]. Proceedings of the Institution of Mechanical Engineers Part F-Journal of Rail and Rapid Transit, 2018, 232(4): 1033−1048.
[10] 杨光, 任尊松. 基于弹性模型的高速列车曲线通过时轮轨接触特性研究[J]. 机械工程学报, 2018, 54(4): 132−141. YANG Guang, REN Zunsong. Wheel/rail contact performance on curved track of high-speed EMU with elastic model[J]. Journal of Mechanical Engineering, 2018, 54(4): 132−141.
[11] Brown M A, Shabana A A. Application of multibody methodology to rotating shaft problems[J]. Journal of Sound and Vibration, 1997, 204(3): 439−457.
[12] 李国芳, 岳鹏, 丁旺才, 等. 轮对柔性对车辆动态曲线通过性能的影响研究[J]. 铁道标准设计, 2019, 63(9): 173−179. LI Guofang, YUE Peng, DING Wangcai, et al. Research on the influence of flexibility wheelset on vehicle dynamic curve passing performance[J]. Railway Standard Design, 2019, 63(9): 173−179.
[13] 翟婉明. 车辆−轨道耦合动力学[M]. 3版. 北京: 科学出版社, 2007. ZHAI Wanming. Vehicle-railway coupling dynamics[M]. 3rd ed. Beijing: China Science Press, 2007.
[14] Piotrowski J, Kik W. A simplified model of wheel/rail contact mechanics for non-Hertzian problems and its application in rail vehicle dynamic simulations[J]. Vehicle System Dynamics, 2008, 45(1−2): 27−48.
[15] TB10621—2014, 高速铁路设计规范[S].TB10621—2014, Code for design of high speed railways[S].
[16] 铁运[2008]28号, 高速动车组整车试验规范[S]. Railway[2008] No. 28, Test specification for high speed emus [S].
The influence of wheel flat on the performance of high-speed vehicle dynamic on railway curve negotiation
WANG Xiangping, WANG Hongbing, JIA Wenhui, LI Guofang, DING Wangcai
(School of Mechatronic Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)
To explore the influence of wheel flat on the dynamic curve negotiating of high-speed vehicles, the relationship between the length and depth of the old flat was deduced, a vehicle-track rigid-flexible coupling dynamic model based on wheelset flexibility was established, on the basis of fully considering the elastic deformation of wheel set, the influence law of the size change of new and old flat on the negotiation of the curve was analyzed. The results show that the bogie two wheels have the biggest influence on the vehicle curve passing due to the flat on the inner rail side wheels; the larger the size of the new flat, the more unfavorable it is for the curve to pass; the influence of the extension of the old flat along the depth on the curve passage is greater than that along the length; when the inner rail side wheels are under high elevation, the wheel and rail abrasion, derailment coefficient and lateral force of the wheel-rail are greater, overturning coefficient and vertical force of wheel and rail are larger when the height is too high; the impact of flat on vehicle curve passage is mainly reflected in the damage to the curve line structure. It is suggested to establish the limit of wheel rotation with flat based on the vertical force peak of wheel- rail.
high-speed vehicle; wheel flat; curve negotiation; rigid-flexible coupling; dynamics
U270
A
1672 − 7029(2020)09 − 2198 − 10
10.19713/j.cnki.43−1423/u. T20191144
2019−12−17
国家自然科学基金资助项目(11962013);兰州交通大学−天津大学联合创新基金资助项目(2019059)
丁旺才(1964−),男,甘肃天水人,教授,博士,从事车辆工程与非线性动力学研究;E−mail:dingdd@163.com

(编辑 涂鹏)

