矿区废弃地移动机器人全覆盖路径规划

周林娜，汪 芸，张 鑫，杨春雨

中国矿业大学信息与控制工程学院，徐州 221000✉通信作者，E-mail：chunyuyang@cumt.edu.cn

土地资源是人类生存和发展的载体，是进行农业生产和工业建设的基础物质条件，但我国人口众多，人均用地严重不足，人地矛盾是我国面临的主要矛盾之一. 改革开放以来，煤炭的过度开采占用大量土地，矿区周边土壤质量恶劣. 大量数据表明：矿区废弃地复垦是缓解农业用地、改善矿区生态环境的重要途径[1]. 矿区废弃地环境复杂，土地复垦存在很大难度，土地复垦的前提是对矿区土壤的全覆盖采样. 移动机器人由于具备环境感知、行为决策及运动控制等能力，被广泛用于智能清洁、农田作业、军事探测等领域的全覆盖作业[2].为推进煤矿安全发展，国家煤矿安全监察局于2019年提出了大力研发应用煤矿机器人的目标.本文面向矿区废弃地复垦的国家需求，研究移动机器人全覆盖路径规划问题.

矿区废弃地土壤质量恶化，面临严重的生态问题，其非结构化的环境基础对移动机器人全覆盖路径规划提出挑战. 全覆盖路径规划是指机器人按照一定工作方式，在具有障碍物的环境中，无碰撞地遍历除障碍物以外的全部区域[3]. 根据对环境信息的已知程度，全覆盖路径规划可分为信息已知的全局路径规划和信息未知的局部路径规划[4]. 未知环境下的完全遍历路径规划方法主要包括随机遍历法、漫步式探测法和沿边规划策略.随机遍历法是一种基于无环境模型的路径规划方法，该方法清扫过程简单但会造成重复率高及清扫时间过长等问题. 漫步式探测方法主要包括动态窗口法，该方法能够完成避障，实现环境的完全覆盖，但时间成本高. 沿边规划策略首先采用沿边学习建立环境模型，然后与局部路径规划相结合遍历整个未知环境，生物激励神经网络（Biologically inspired neural network, BINN）算法[5−7]是一种基于沿边规划策略的方法，可以很好地应用于动态未知环境.

矿区废弃地的先验环境信息通过遥感卫星系统获得，移动机器人的主要任务是对矿区实施全覆盖从而获得土壤采样信息，基于以上特点，本文研究已知矿区环境全覆盖路径规划问题. 已知环境下的完全遍历路径规划算法主要包括模板模型法[8]和单元分解法[9]. 模板模型法通过将获取的环境信息与各个模板匹配来完成遍历，对环境缺乏整体规划，难以适应变化的环境. 单元分解法将整个环境的复杂度简化为子区域内环境的复杂度，在大型已知环境下被广泛应用，主要包括梯形单元分解法[10−11]、牛耕式单元分解(Boustrophedon cellular decomposition, BCD)法[12]和莫尔斯单元分解法[13]. BCD方法分解完成之后的子区域较少，本文采用BCD方法对环境做区域分解. 单元分解完成之后需要确定子区域内部覆盖方式，为应对未知障碍物的出现，本文采用BINN算法完成移动机器人对子区域内部的覆盖. 移动机器人在当前子区域内部覆盖完成之后需要转移到下一子区域，点对点路径规划具有巨大作用. Wang等[14]将Dijkstra算法应用到机器人路径规划算法方面，该算法在迷宫环境中能够获得两点间的最短路径.Fu等[15]对A*算法进行改进并应用于工业机械臂，该改进A*算法能够缩短路径规划距离. Wei和Ren[16]在机械臂上采用快速搜索随机树(Rapidlyexploring random trees, RRT)算法，可以完成静态障碍物和动态障碍物的避障，但并不能获得最短路径. Rashid等[17]采用蚁群算法解决简单环境地图和复杂环境地图中的移动机器人路径规划问题.张超等[18]提出了一种新的基于粒子群的改进蚁群算法，该算法采用全局异步与精英策略相结合方法更新信息素，减少了路径规划时间. 群智能优化算法能够解决移动机器人路径规划问题，但是此类算法产生的路径平滑性较差. 近年来，BINN算法逐渐被应用到移动机器人路径规划方面，王耀南等[6]通过在边界附近和障碍物之间增加假想非障碍物临近点改进BINN算法，修改路径决策方法，优化了路径质量. Zhu等[7]将BINN算法应用到水下机器人方面，解决了多机器人的任务分配和路径规划问题. 以上文献中的BINN算法均可以被有效应用于移动机器人路径规划方面，但是没有充分利用已知环境信息.

本文根据矿区废弃地先验环境信息，采用BCD结合BINN方法解决移动机器人对矿区废弃地的全覆盖路径规划问题，既包括子区域内部全覆盖路径规划又包括子区域间路径转移. 首先采用BCD方法划分整个非结构化的环境，然后通过深度优先搜索（Depth first search, DFS）算法确定子区域间遍历顺序，最后采用BINN算法完成子区域内部覆盖和子区域间路径转移，从而实现矿区全覆盖.

1 矿区废弃地基本环境及假设

矿区废弃地是指矿山开采过程中失去经济利用价值的土地，也指在采矿期间任何没有经过人为修复的土地. 矿区废弃地存在大量煤矸山、废弃厂区以及踩空塌陷区和积水区等，这些特点造成了矿区废弃地环境的复杂性. 图1为国内某矿区废弃地现状图，矿区废弃地的先验环境信息由遥感卫星系统获得，但是环境中可能存在部分未被感知区域，导致矿区废弃地环境复杂. 图2为矿区废弃地复杂障碍图.

图1 废弃矿区现状Fig.1 Status of abandoned mine land

图2 废弃矿区复杂环境. （a）积水区；（b）废弃厂区；（c）尾矿、煤矸石的堆占；（d）周边土壤现状Fig.2 Complex environment of abandoned mine land: (a) pools zone;(b) abandoned factory; (c) heap of tailings and gangue; (d) status of surrounding soil

为了实现非结构化矿区废弃地环境移动机器人全覆盖路径规划的遍历且减少重复覆盖，根据以上实际情况，对环境做如下假定：

（1）假定该矿区废弃地环境全局信息已知；

（2）假定环境中的障碍物存在复杂性，即同时存在规则障碍物和非规则障碍物；

（3）在做仿真实验时，假定煤矸山为三角形障碍物，废弃厂区为多边形障碍物，矿区积水区及其他复杂障碍物以非规则障碍物表示.

2 矿区废弃地全覆盖路径规划

矿区废弃地为室外大型非结构化环境，移动机器人对该环境的路径规划存在较大难度. 目前矿区环境下的移动机器人研究任务多为点对点路径规划[19−20]，本文将采用区域分解法[21−22]实现全覆盖路径规划，主要包括三个部分：目标区域分解、子区域规划和各子区域遍历. 具体流程如图3所示.

图3 全覆盖路径规划流程图Fig.3 Flow chart of complete coverage path planning

2.1 目标区域分解

单元分解法[9]是一种运动规划技术，该方法将所有自由支配空间分解为多个单元，使得所有单元联合起来是原始自由空间. 传统单元分解法是梯形单元分解法[10]，BCD方法[12]在梯形单元分解法上进行改进，该方法假设一条垂直线（被称作切片）从左到右扫过一个充满多边形障碍的有界环境，每遇到顶点可上下延伸的临界点便进行分割，最终环境被分割为多个不含障碍物的子区域. 相比梯形单元分解法，BCD方法产生更少的子区域，可以减少机器人的路径冗余，进一步降低能源消耗和时间损耗. 因此，BCD方法适合矿区废弃地环境. 表1给出了BCD方法的步骤.

表 1 BCD 方法步骤Table 1 BCD method steps

图4（a）为矿区废弃地仿真环境，该环境具有复杂性，包括规则几何障碍物和非规则障碍物，采用BCD方法对该环境做区域分解，分解结果如图 4（b）所示. 其中，C1～C10 为分解后的 10 个子区域.

图4 矿区废弃地仿真图. （a）仿真环境；（b）区域分解图Fig.4 Simulation map of abandoned mine land: (a) simulation environment; (b) regional decomposition map

本文所使用的BCD方法能够有效分解具有综合复杂性的环境. 实验证明，该方法可以被广泛应用于矿区废弃地等复杂室外环境，它能够有效减少机器人在室外做全覆盖路径规划的难度.

2.2 子区域规划

区域分解完成之后，机器人可通过两个步骤完成对整个区域的覆盖：（1）在邻接图中找到一个详尽的行走顺序，该覆盖顺序可以指导机器人到达工作空间中所有可到达的子区域；（2）完成子区域内部覆盖以及区域间的转移. 本模块主要完成子区域遍历顺序规划，采用的算法为DFS算法.

DFS算法[23]是图论中最著名的一种搜索算法，该算法经常被用来遍历图中所有点，找到一条可供行驶的详尽覆盖路径. 表2为该算法步骤.

表 2 DFS 算法步骤Table 2 DFS algorithm steps

图5 子区域连接图. （a）邻接图；（b）转移序列图Fig.5 Connection diagram of subregions: (a) adjacency map; (b)transfer order map

将BCD 方法中切片的运行方向定义为从左往右，图5（a）为区域分解完成之后的子区域构成的邻接图，根据切片运行方向，将A设置为起始点，图5（b）即为使用DFS算法规划的子区域顺序结果图. 图5（b）中，A为机器人遍历的第一个子区域，当A遍历结束时机器人从该区域结点到转移下一个子区域B的起始点，对B区域内部进行全覆盖遍历，以此类推，直至到达最后一个子区域C的结点.

2.3 各子区域遍历

2.3.1 BINN 算法

BINN算法是一种在线规划算法，该算法将每个栅格看作一个神经元，整个栅格地图变为由神经网络组成的拓扑状态空间，其中神经元的活性值由下式表示：

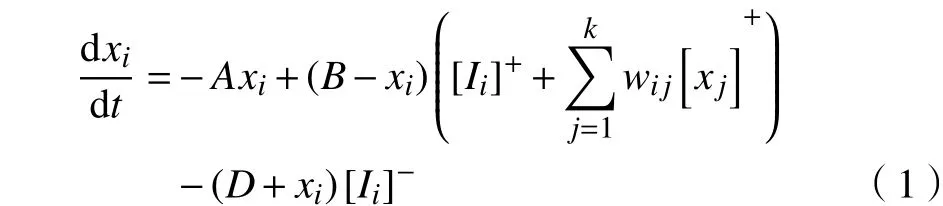
式（1）为分流方程[24]，通过该方程可以计算出栅格地图中每个神经元的活性值. 式中：为 第i个神经元的活性值；t是时间量；、和为非负常数，其中代 表衰减率，代表神经元活性状态的上限，代表神经元活性状态的下限；为与第i个神经元直接连接神经元的个数；为外部输入，可定义为：

其中：E是一个远远大于B的正常数；和分别表示兴奋输入和抑制输入是第i个神经元与第个神经元所在位置处在状态空间中的欧几里得距离，为任意的单调减函数，可定义为

BINN算法既可以完成点对点路径规划又可以完成全覆盖路径规划. 机器人生成点对点的路径为：

该路径生成过程为：机器人在当前位置选择邻接神经元中具有最大活性值的神经元栅格作为下一位置，到达下一位置后，下一位置成为新的当前位置，以此类推，直到到达目标点栅格. 如果周边8个邻接神经元的活性值都不大于当前栅格的神经元活性，则机器人待在原地保持不动，机器人陷入死区.

机器人生成全覆盖的路径为：

图6 BINN 算法流程图Fig.6 Flow chart of BINN algorithm

2.3.2 子区域内部遍历

在区域分解和子区域遍历顺序确定后，关键步骤是完成对子区域内部的遍历. BINN算法是一种在线规划算法，不需要学习过程，适合处理未知情况. 由于矿区废弃地结构复杂，环境中可能存在未知障碍物或移动障碍物等一系列现象，为了在后期的工作中能够较好地应对突发状况，本文采用BINN算法完成对每个子区域内部全覆盖.

2.3.3 区域路径转移

当前子区域内部覆盖完成之后到下一子区域内部覆盖之前需要子区域间的路径转移，从而使移动机器人按照子区域规划序列完成对所有子区域的覆盖. 针对该问题，本节主要使用BINN算法规划从上一个子区域遍历终点到下一个子区域遍历起点的最短路径搜索，并计算该算法在最短路径和时间消耗方面的总代价. 因此，定义一系列由点组成的转移路径：

其中，a代表神经元的横坐标，b代表神经元的纵坐标.

本文所提出方法同样适应于室内具有综合复杂性的环境.

3 仿真实验

本文的内容应用于移动机器人矿区废弃地环境路径规划. 本节分别对子区域内部遍历和子区域间路径转移进行仿真实验，其中路径转移实验中BINN算法和其他路径规划算法同时进行. 实验方案规划：首先，对工作环境进行栅格地图建模，建立分区之后的环境模型；其次，采用DFS算法规划子区域遍历序列；最后，采用BINN算法完成对每个子区域内部的覆盖以及子区域间路径转移，并与其他路径规划算法做对比仿真实验. 仿真实验如下所示.

3.1 参数设置与仿真环境

为了验证BINN算法做全覆盖路径规划时的效果，设计相关仿真实验，合理参数设置和仿真实验环境设定是确保实验成功的重要环节，本文参数设置环节依据文献[25]，并根据实验环境做了相应调整. 本文设定栅格地图，在该栅格地图中自由栅格值为1，障碍栅格值为，和代表的是神经活性上界与下界，和取1和；代表外部输入，远远大于和，将的取值设为；代表神经元活性衰减速率，本文取；代表方向权重的选择，在全覆盖路径规划中，的选择会影响机器人路径决策，为平滑机器人的路径，将的值取为1；代 表当前神经元与周边神经元活性之间侧向连接，对当前神经元的活性值有较大影响，在做全覆盖路径规划时为获得规则路径，值 取1，在做点对点路径规划时考虑到目标神经元的导向作用，根据不同环境重新设定.

本文中的仿真实验均在Matlab R2017b中进行，7.9 GB 计算机内存，3.41 GHz CPU 速度.

图7 子区域遍历结果. （a）全覆盖结果；（b）路径转移结果Fig.7 Coverage results of subregions: (a) complete coverage result; (b) path transition result

3.2 子区域遍历实验

在图7（a）中，环境中的障碍物形状各异，机器人从初始位置（2,2）开始运动，根据仿真结果可知，该算法能够在这种复杂环境下做出相应的路径选择策略，并且在每一个子区域内部完成全覆盖. 本例子中区域重复覆盖率为0，总覆盖面积达到100%，有效证明了该算法的可行性. 从图 7（a）中可以看到虚线经过了障碍物栅格，路径转移算法需要完成避障功能. 三个部分路径转移的实施离不开点对点路径规划算法，本模块BINN算法在做点对点路径规划时，在目标点处增加了神经元活性值，并在三个区域转移部分分别设置不同的来减少路径的转折，优化算法的搜索路径. 实验结果证明算法实现了自主避障并有效搜索到了目标点，路径没有出现跨越和迷失现象，该算法在点对点路径规划中具有高效性.

3.3 对比实验

为证明BINN算法在区域转移方面的性能，本文选用几种经典点对点路径规划算法与BINN算法做对比试验. 通常情况下，路径转移距离和路径转移时间是衡量覆盖任务的重要指标. 路径转移距离为机器人从上一个子区域结点到下一个子区域起始点生成的路径距离；路径转移时间为完成这项任务消耗的时间，通过这两种性能指标来评价两种算法最短转移路径的总代价.

图8 实验结果对比. （a）BINN 算法；（b）A*算法；（c）Dijkstra 算法；（d）RRT 算法Fig.8 Comparison of experimental results: (a) BINN algorithm; (b) A* algorithm; (c) Dijkstra algorithm; (d) RRT algorithm

本小节选用的对比算法为A*算法、Dijkstra算法和 RRT算法. BINN算法、A*算法、Dijkstra算法均是基于栅格地图，路径转移距离为所有栅格之间的欧氏距离之和；RRT算法基于坐标地图，路径转移距离为所有坐标点之间的距离之和，栅格地图与坐标地图具有对应性，因此几种算法路径长度具有可比性. 图8、表3、表4和图9展示了四种算法对比实验结果. 图8中BINN算法路径用“×”表示，A*算法路径用“○”表示，Dijkstra算法路径用“△”表示，RRT算法路径用“·”表示.

表 3 路径转移距离对比Table 3 Distance comparison of path transition

表 4 路径转移时间对比Table 4 Time comparison of path transition

从图 9（a）和表 3 可以得出，在 J—I，I—F 区域中，BINN算法生成的路径长度和A*算法、Dijkstra算法相同，小于RRT算法的路径长度；F—C区域中BINN算法的路径长度最小，因此，总路径长度BINN算法最小. 本文在区域转移部分应用BINN算法时增大了目标点神经元活性，引导算法快速搜索目标神经元，同时根据对的不同设定，缩短了规划路径，该算法获得最短搜索路径. 根据图9（b）和表4，在三个区域转移部分，由于BINN算法对目标神经元的导向作用，算法快速搜索到目标神经元位置，BINN算法消耗的时间最少. 从上述实验结果中可以看到，在路径转移距离方面，BINN算法在J—I区域，I—F区域，F—C区域均获得最小的总路径；在路径转移时间方面，BINN算法的路径转移时间代价最小. 因此，不论路径转移距离还是路径转移时间，BINN算法均最优.

图9 算法性能评价结果图. （a）距离对比结果；（b）时间对比结果Fig.9 Performance evaluation results of algorithms: (a) distance comparison result; (b) time comparison result

4 结论

针对矿区废弃地等复杂环境，本文使用BCD方法结合BINN算法完成移动机器人对整个环境的全覆盖. 本文将BINN算法用于区域分解中，既能够实现机器人对子区域内部全覆盖又能完成子区域间路径转移. 仿真实验结果验证了本文所使用的方法的可行性. 在路径转移方面，本文使用三种点对点路径规划算法做对比实验，实验结果证明，不论是在路径转移距离方面还是在路径转移时间方面，BINN算法均具有高效性. 未来的工作任务是采用一种主动搜索算法完成下一子区域最佳起始点的搜索，要求该搜索算法获得的最佳起始点与上一结点之间具有较短路径消耗.