基于融合模型的锂离子电池荷电状态在线估计

王晓兰，靳皓晴，刘祥远

1) 兰州理工大学电气工程与信息工程学院，兰州 730050 2) 甘肃省先进工业过程控制重点实验室，兰州 730050 3) 兰州理工大学电气与控制工程国家级实验教学示范中心，兰州 730050✉通信作者，E-mail：wangzt@lut.cn

在全球应对环境污染及气候变化的大背景下，各国开始重视能源体系变革和经济发展方式向低碳转型，其中发展低碳交通已成为绿色交通建设的重要内容[1]. 而电动汽车，特别是纯电动汽车技术的发展，能够有效降低能源消耗，减少环境污染. 目前，具有能量密度高、单体电压高等优点的锂离子电池已被广泛作为电动汽车的储能部件使用[2]. 然而，随着近年来国内外不断报道的新能源汽车的安全事故问题，使锂离子电池的安全问题越来越受到业界的关注[3]. 为防止使用过程中的过充、过放影响电池的使用寿命及使用安全，需要一套完善的电池管理系统（Battery management system，BMS）对锂离子电池进行控制及管理，而用来反映电池剩余容量状况的荷电状态（Stage of charge，SOC），是其中关键的参数之一[4]，因此，准确的SOC值对锂离子电池的使用安全及新能源汽车的安全性能都具有重要的意义[5]. 然而，锂离子电池的SOC值无法直接用传感器进行测量，为此，需要对锂离子电池SOC值进行准确的估计，以保证BMS系统的可靠运行.

常用的SOC估计方法包括[6]：放电实验法、安时积分法、开路电压法、等效电路模型法和机器学习法. 放电实验法需要将电池进行长时间的静置处理，无法在实际工程中投入使用；安时积分法计算简单，但仅考虑电池电流一个影响SOC值的因素，且随着工作时间增加，测试电流的误差会不断累计，使得此方法精度越来越低，无法长时间独立使用[7]；开路电压法也要在电池经过长时间静置的条件下进行，无法直接实现工程应用[8]. 相比之下，基于等效电路模型的SOC估计方法，可以通过建立等效电路模型表征电池的动静态特性，并根据等效电路模型推导出状态空间方程，结合扩展卡尔曼滤波（Extended Kalman filtering，EKF）等算法来研究电池电压、电流、内阻以及温度等多种外特性对SOC估计值的影响，适用于动态工况，尤其是电流变化较快的动力电池[9]. 当前常见的等效电路模型包括Rint模型[10]、RC模型[11]和Thevenin模型[12]. Rint模型是电池的初始等效电路模型，无法体现电池的动态特性，因此在实际工程中并不适用；RC模型虽然具有较高的精确度，但在使用时需要已知电池的极化电压，且该电压无法直接测量，因此RC模型也未能得到广泛应用；而Thevenin等效电路模型不仅可以体现锂离子电池的动静态特性，且应用时只需对电池电压、电流进行测量，因此该模型在实际工程中得到了广泛地应用. EKF算法是一种通过利用线性化技巧将非线性滤波问题转化为近似线性滤波问题的算法，可解决SOC初值不准的问题，具有较高的估计精度，近年来，EKF算法已被广泛应用于锂离子电池SOC 估计中[13–14]. 当前研究表明，Thevenin 等效电路模型结合EKF算法可对SOC进行较准确的估计，且增加Thevenin等效模型的阶数可有效提高模型精度，然而，采用高精度的等效电路模型虽然可以获得具有更高精度的SOC估计值，但随着等效电路模型精度的增加，模型的复杂度也随之增加，继而增加了状态空间方程的推导难度及方程自身的复杂度，使得在实际应用中对SOC估计值的计算难度大幅增加，且传统EKF算法的参数为定值，也会对估计结果产生一定影响[15–18]. 除此之外，电流、电压的测量误差同样会降低SOC估计精度. 相对于等效电路模型法，机器学习法摆脱了物理模型的约束，仅通过学习输入输出数据，即可建立预测模型，直接对电池SOC进行估计. 常用的机器学习法包括 BP（Back propagation）神经网络法、支持向量机法（Support vector machine，SVM）以及极限学习机（Extreme learning machine，ELM）法. 研究结果表明，基于ELM算法建立的模型误差精度保持在4%以内，且相比于BP神经网络及SVM算法，ELM算法具有精度高、训练时间短和参数设置简单的优势[19–22]. 而文献[23]中也分别对BP神经网络法、SVM法以及ELM法做了详细的对比分析，进一步说明了ELM算法在预测模型中的优势，此处不再过多赘述. 理论上，只要拥有充足且高质量的训练样本，ELM算法即可对锂离子电池SOC值进行高精度估计，但在实际应用中，样本数据的质量、数量及ELM算法本身都会影响预测结果的精确度，且电池的端电压、电流、内阻以及SOC值之间存在一定的物理联系，因此，结合物理模型更有利于得到高精度的SOC估值.

针对现有锂离子电池SOC估计方法的研究，为进一步提高锂离子电池SOC在线估计的精度，减小传统EKF算法因参数固定对估计结果产生的误差，解决等效电路模型复杂度以及电流、电压的测量误差对SOC估计造成的影响，本文对影响锂离子电池SOC估计值的主要因素（电池电压、电流）进行基于等效电路模型法的研究，保留电池电压、电流与SOC之间的物理联系，并对EKF算法进行改进，随后将影响SOC估计值的次要因素（模型复杂度及电压、电流传感器测量误差）考虑在内，并利用ELM算法表征其对SOC估计值的影响，建立了适用于一阶Thevenin等效电路模型的SOC误差预测模型，并以该模型的输出结果为补偿项对等效电路模型法的SOC估计结果进行误差校正，最终建立了基于物理–数据融合模型的锂离子电池SOC估计方法，解决了因EKF算法参数恒定、电路模型复杂度以及电流、电压的测量误差对SOC估计造成的影响，进一步提高了SOC在线估计的精度.

1 电池放电试验

美国先进电池联合会（USABC）给出的SOC定义如式（1）所示[24]，其中为SOC，为当前电池的剩余电量，为额定容量.

为获取电池电压、电流及SOC标准值，本文利用MATLABSimlink中自带的锂离子电池充放电模型进行放电试验，其中，锂离子电池模块原理如图1所示，为 指数电压；为指数容量；为电池额定电压；为 非线性电压；为电池额定容量；为当前时刻电池容量；为电池电流；为低频电流；IC为放电电流；UL为电池端电压；为电池内阻. 放电电流IC通过电流控制模块对电池进行放电，由电池端电压UL与电池内阻R求得电池电流I，通过安时积分法得到当前时刻的电池容量，代入式（1），即可得到当前时刻电池的SOC值.本文所用电池参数如下：E0= 3.7 V，Q= 12 A·h，=0.0056 Ω，IC为UDDS工况下两组不同的放电电流.得到两组电池电流I、电压UL及SOC值如表1、表2所示，两组各2000个数据点，在下文结果分析中，将表1及表2中所得SOC值作为标准值

图1 电池模块原理图Fig.1 Schematic of the battery module

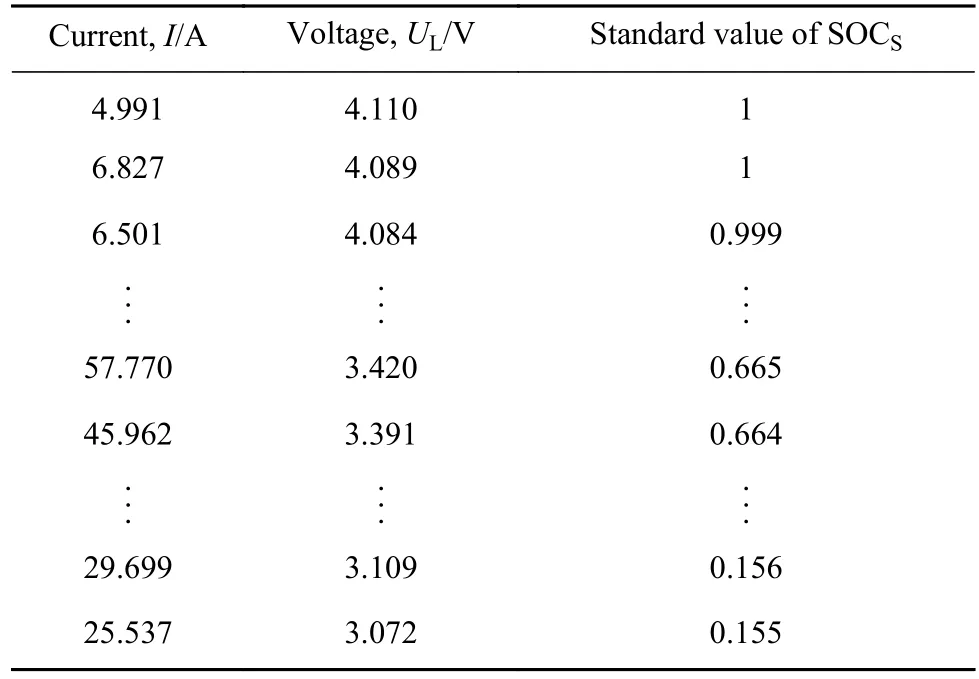
表 1 第一组放电试验数据Table 1 First set of discharge data

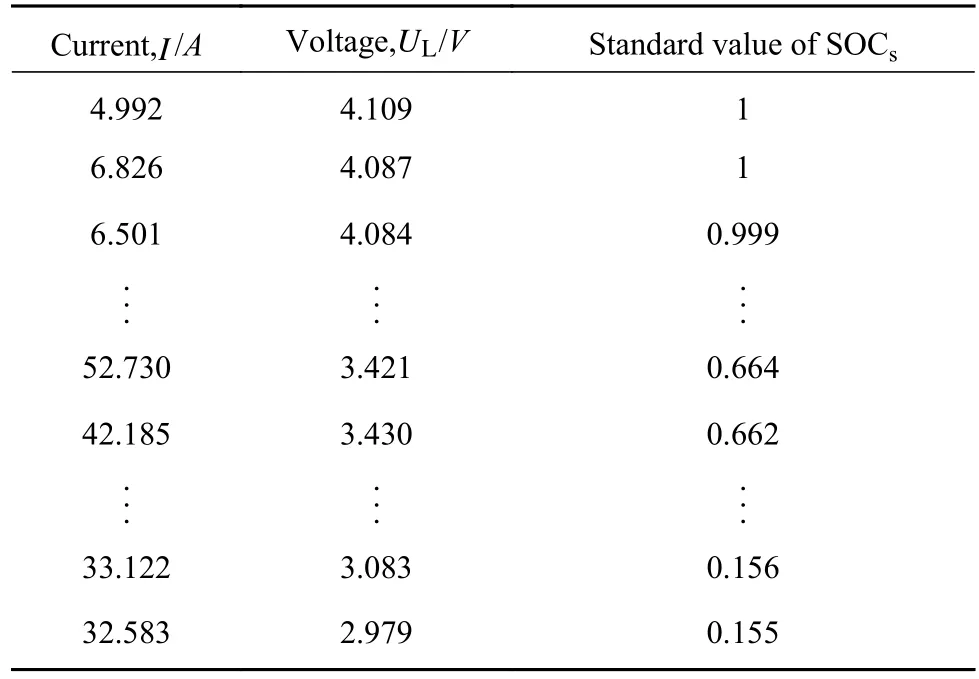
表 2 第二组放电试验数据Table 2 Second set of discharge data

2 等效电路模型的选取

本文选取一阶Thevenin等效电路作为等效电路模型，其结构如图2所示，其中为欧姆内阻；为极化电阻；为 电池端电压；为极化电容；为SOC值；为电池额定容量；为电容两端电压；表示开路电压与SOC之间的函数关系. 该模型考虑了储能电池与电容有相似之处的特点，将电池等效为电压源与电阻及RC网络串联的形式，其离散状态方程和输出方程分别如式（2）和（3）所示，其中T表示采样时间.

图2 一阶 Thevenin 等效电路模型Fig.2 First-order Thevenin equivalent circuit model

文献[25]中锂离子电池放电实验的结果，得到一阶Thevenin等效电路模型参数如表3所示：

表 3 一阶 Thevenin 等效电路模型参数Table 3 Parameters of the first-order Thevenin equivalent circuit model

3 SOC 估计的等效电路模型法及其误差预测模型的建立

3.1 基于改进 EKF 算法的 SOC 估计

为提高等效电路模型法的SOC估计精度，本文在一阶Thevenin等效电路模型的基础上建立状态空间方程，并采取改进EKF算法对SOC进行估计.

由图2可知：

（2）预测状态变量：以电池电压、电流为输入，根据式（5），得到状态变量的先验值

（7）重复步骤（2）至（6）.

由于影响EKF算法估计精度的主要因素为Q、R以及矩阵A的取值，而矩阵A为确定的量，为提高SOC估计精度，减小传统EKF算法因参数固定对估计结果造成的误差，本文对参数、进行动态选择. 由于安时积分法计算简单，且在线应用时具有较高精确度，本文将式（5）中得到的SOC先验值与通过安时积分法得到的当前SOC值进行比较，根据与安时积分法得到的估计值之间的差值大小不同判断先验值的准确性，以此选取不同的、值，进而改变先验值在SOC估计计算中的占比. 其中安时积分法方程如式（10）所示，其中为k时刻电池电流：

图3 改进 EKF 算法估计 SOC 流程图Fig.3 Flowchart of the improved extended Kalman filtering (EKF)algorithm used to estimate the state of charge (SOC)

以表2中所得电池电流、电压为输入，得到以一阶Thevenin等效电路为模型时，传统EKF算法与基于改进EKF算法的SOC估计误差的对比，如图4所示. 由图中曲线可以看出，改进后的EKF算法得到的SOC估计值的绝对误差基本保持在0.04以内，而传统EKF算法对SOC估计值的绝对误差最大值达到0.08，可见，改进EKF算法有效的提高了SOC估计的精度.

表4所示为传统EKF算法与改进EKF算法在估计SOC时的均方误差对比，由表可知，由改进EKF算法得到的SOC估计值的均方误差较传统EKF算法的均方误差减小了55%，进一步说明了改进EKF算法对提高SOC估计精度的有效性.

图4 EKF 算法误差对比曲线Fig.4 Error contrast curve of the EKF algorithm

表 4 传统EKF算法与改进EKF算法均方误差对比Table 4 Comparison of the mean squared error between the traditional and improved extended Kalman filtering (EKF) algorithms

3.2 SOC 误差预测模型的建立

为建立适用于等效电路模型法的SOC估计误差的预测模型，首先需要求得以一阶Thevenin电路为模型时SOC的估计误差. 本文以表1和2中两组电池电压、电流为输入，按图3所示流程图进行计算，得到两组以一阶Thevenin等效电路为模型时的SOC估计结果，再分别以表1、表2中对应SOCS为标准值，代入式（11），得到两组SOC估计的绝对误差σ，如表5所示.

由文献[27]和[28]可知，不同于其他机器学习法，ELM算法在使用时只需给定隐含层神经元个数及激活函数即可获得如式（12）所示的误差预测模型.

图5所示为基于ELM算法训练得到的SOC误差预测模型结构图，其中电池电压、电流为输入值，SOC估计误差y为输出值，为输入层和隐含层之间的权值；为输出层和隐含层之间的权值；为隐含层神经元阈值.

图5 基于 ELM 的 SOC 误差预测模型结构Fig.5 Structure of the SOC error prediction model based on the extreme learning machine algorithm

本文以表1中所得电池电流、电压作为训练样本的输入，以表5中第一组σ值作为训练样本的输出，采用式（13）的方法，将数据进行归一化处理，其中为 第i个数据，为数据中的最小值，为数据中的最大值，为归一化后得到的数据.

表 5 SOC 估计绝对误差Table 5 Absolute error of the state of charge estimation

将Sigmoidal函数设为隐含层激活函数，且由于第一小节中的电池放电仿真获得了两组不同的电压、电流以及SOC标准值各2000个，而对于极限学习机来说，当隐含层神经元个数与输入数据个数相同时，训练得到的模型精度较高，因此，为获取具有较高精度的误差预测模型，本文将隐含层神经元个数设为与输入数据个数相同的2000进行训练，得到适用于一阶Thevenin等效电路模型的误差预测模型，以表2中所得电池电压、电流值与表5中第二组σ值为测试数据，对基于ELM的误差预测模型进行测试，得到误差预测模型性能如表6所示.

图6所示为误差预测模型的测试误差曲线，由图可知，基于ELM建立的误差预测模型在测试集上得到的绝对误差始终保持在0.03之内，说明了本文基于ELM算法建立的误差预测模型具有较高的精确度.

表 6 基于 ELM 的误差预测模型性能Table 6 Error prediction of model line performance based on the extreme learning machine algorithm

图6 预测模型在测试集下的绝对误差值Fig.6 Absolute error of the prediction model under the test set

4 基于融合模型的 SOC 在线估计及结果分析

为进一步提高SOC估计的精度，解决等效电路模型法中由电流、电压测量所引入的误差，改善等效电路模型法估计精度与模型复杂度相矛盾的问题. 本文根据误差校正的思想，将误差预测模型的输出结果作为通过等效电路模型法得到的SOC估计结果的补偿项，建立了基于物理−数据融合模型的锂离子电池SOC在线估计方法，下文简称融合模型法，如式（14）所示：

图7所示为融合模型法的结构图，由等效电路模型与误差预测模型两部分组成，将两种模型的输出结果进行融合，最终得到基于融合模型的锂离子电池SOC在线估计值.

图7 融合模型法系统结构图Fig.7 System structure diagram of the fusion model method

图8 绝对误差对比Fig.8 Comparison of the absolute errors

为对融合模型法估计结果做出进一步对比，本文又以二阶Thevenin等效电路为模型，建立输入输出方程，利用改进后的EKF算法进行SOC估计.

图9 二阶 Thevenin 等效电路模型Fig.9 Second-order Thevenin equivalent circuit model

表 7 二阶 Thevenin 等效电路参数Table 7 Parameters of the second-order Thevenin equivalent circuit model

表 8 不同模型估计结果对比Table 8 Comparison of the estimation results of different models

图10 SOC 估计曲线对比Fig.10 Comparison of the SOC estimation curves

5 结论

本文首先对传统EKF算法进行改进，提高了算法的估计精度. 其次，本文基于ELM算法建立了适用于以一阶Thevenin电路为模型时等效电路模型法的误差预测模型，该模型可根据电池工作电流、电压对等效电路模型法的SOC估计误差进行预测，将该误差预测值作为校正项对基于一阶Thevenin电路的等效电路模型法的SOC估计结果进行校正，使物理模型和数据模型相融合，建立了基于物理−数据融合模型的锂离子电池SOC在线估计方法. 将该方法所得估计结果分别与以一阶、二阶Thevenin电路为模型时等效电路模型法所得估计结果进行对比，仿真结果表明，本文建立的基于物理–数据融合模型的锂离子电池SOC在线估计方法，结合了等效电路法与ELM法两者的优点，使SOC估计结果的最大百分误差保持在0.09%以内，提高了SOC的估计精度；克服了电流、电压测量误差对SOC估计值的影响；解决了等效电路模型法中SOC估计精度与模型复杂度相矛盾的问题，且满足BMS系统对于SOC估计误差小于5%的要求，在在线SOC估计中具有广阔的应用前景.