基于DBN-DNN的离散制造车间订单完工期预测方法

刘道元，郭 宇，黄少华，方伟光，杨能俊

(南京航空航天大学 机电学院，江苏 南京 210016)

0 引言

目前，产品需求类型急剧增加，更新换代越来越快，从而驱动从按库存生产到按订单生产模式的转变[1]。在按订单生产的企业中，准确的订单完工期预测对合理的生产计划制定、准确的调度排产、按时的产品交付具有重要意义，甚至影响了制造企业的信誉和竞争力[2]。随着自动识别、智能传感、先进控制等技术在离散制造车间的逐步应用，车间在制品转运、设备运行、物料状态等制造数据的采集愈加快速准确[3]，而数据的体量和复杂程度也大大提高，这为订单完工期预测提供了更加完备的数据支撑，同时对预测方法提出了更高的要求。

参考现有文献，订单完工期预测方法主要可以分为仿真、基于案例推理(Case-Based Reasoning, CBR)、统计分析和神经网络等。申建红等[4]将Shapley值函数和仿真技术相结合，根据每道工序的工程量与单位时间完成工作量的比值，计算出每道工序的理想化工期；Vinod等[5]研究了在按订单生产环境下，通过建立仿真模型来评估订单截止日期。Chang等[6]讨论了CBR在晶圆制造截止日期分配问题中的应用；汪俊亮等[7]通过费舍尔Z变换筛选得到强相关特征数据，然后采用CBR方法实现订单交货期预测。Pearn等[8]将晶圆等待加工时间拟合为Gamma分布，计算晶圆加工周期；朱雪初等[9]首先基于ReliefF算法进行特征选择，然后基于支持向量回归(Support Vector Regression, SVR)完成晶圆加工周期预测。Chen等[10]使用模糊反向传播(Back Propagation, BP)神经网络对晶圆加工周期进行预测，并将自组织映射[11]、回归树[12]、模糊C-均值[13]与BP神经网络相结合，通过先聚类再预测的方法提高预测精度；Wang等[14-16]分别设计了基于密度峰值的径向基神经网络、基于熵的特征选择和BP神经网络相结合的预测模型，实现晶圆加工周期预测。在上述方法中，仿真技术通过仿真理想化车间的运行状态预估完工期，但对具有高复杂性和多扰动特性的制造系统而言，仿真模型较难精准地描述全制造过程。CBR融合了数据知识和专家经验，但在复杂的制造系统中难以设计高准确度的知识系统。统计分析虽然计算量小、效率高、方法简单，但统计模型过于简单，历史数据的可靠性、选择方法的科学性对预测准确度影响极大。浅层的神经网络虽然对数据的完整性和可靠性要求不高，但适应复杂映射能力较差，难以作为大规模数据的预测模型。

与仿真技术和CBR相比，在多扰动的制造系统中，制造数据隐藏着车间运行规律，使用海量数据训练的深度学习模型更能拟合车间实际运行状态，预测结果更加接近实际情况；与传统的统计分析和浅层的神经网络相比，深度学习可以从大规模、低价值密度的样本中提取高水平特征，获取有价值知识，且具有更强的泛化能力，对处理大数据问题具有更优越的性能[17-18]。深度学习在制造系统中产品质量预测、订单完成时间预测等方面已经有所应用，Bai等[19]使用深度神经网络(Deep Neural Network, DNN)对复杂制造过程中产品质量进行预测，使用贪婪算法进行无监督特征学习，然后将学习的特征输入回归模型中，完成质量预测；Wang等[20]将订单组成和RFID传感器实时采集的车间在制品信息作为数据集，构建深度神经网络模型，实现订单完成时间预测。

本文针对复杂离散制造车间中产生的海量、多源、动态制造数据，提出一种基于深度置信网络(Deep Belief Network, DBN)—DNN的订单完工期预测方法。通过构建ReLU激活的DBN特征提取模型，改善模型准确度和收敛速度，避免过拟合问题。为了进一步提高模型的泛化能力，在回归预测模型中加入dropout和L2正则化。结合某航天车间的生产数据进行实例验证，并与多隐含层BP神经网络、主成分分析和BP神经网络的结合、主成分分析和支持向量回归的结合3种常用的预测模型进行对比分析，验证了本文所提方法的准确度和适用性。

1 问题描述

假定某制造车间有M台机床，用于生产N种不同类型的零件，不同零件的加工路线和加工时间各异，零件的生产遵循以下原则：每个产品的加工工艺路线是确定的；每台机器只加工在制品的一个操作；在生产过程中，操作者选择入缓存区在制品进行加工和出缓存区在制品进行运输时，遵循先入先出的原则。

基于上述条件，定义订单完工期为从订单下达车间开始到最后一个在制品完成离开车间的整个时间长度，即OCT=Tout-Tin。式中：OCT表示订单完工期，Tout表示订单中最后一个在制品加工完成离开车间的时刻，Tin表示订单下达车间的时刻。订单完工期由等待时间、准备时间、加工时间、检测时间、运输时间和返工时间组成。在制品等待时间的主要影响因素包括出/入缓存区排队队列，零件类型；在制品的加工时间主要影响因素包括设备的加工状态、零件的类型和数量；返工时间的主要影响因素是零件类型以及产品的合格率；在制品准备加工时间和检测时间的主要影响因素包括工作人员的熟练程度和零件复杂程度，一般变化不大，设定为常数；运输时间的主要影响因素包括车间布局和车辆运输状态，设定为常数。

综上所述，将订单完工期影响因素归纳为以下3类：

(1)订单组成 零件的种类和数量决定了订单间的差异性。如式(1)所示：

P=[P1,P2,…,PN]。

(1)

式中：P表示订单的产品种类和数量，Pi表示第i种零件数量。

(2)在制品信息 订单任务下达时刻(t时刻)在制品的种类、等待队列等因素直接关系着在制品的加工顺序，并隐藏着零件的加工工艺路线等信息，对订单完工期具有重要的影响[21]。如式(2)所示：

c=1,2,…,M。

(2)

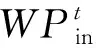
(3)机床运行信息 机床的不确定性影响着车间的生产进度。如式(3)所示：

(3)

基于以上分析，设计预测特征数据集如式(4)所示：

c=1,2,…,M。

(4)

式中CFS表示订单完工期预测的候选特征集。

通过以上介绍的CFS，使用深度神经网络拟合公式(5)完成订单完工期预测：

OCT=f(CFS)。

(5)

式中f表示CFS与OCT之间的对应关系。

2 基于DBN-DNN的订单完工期预测

基于DBN-DNN的订单完工期预测模型步骤如图1所示。首先，将原始数据进行归一化处理，随机选取其70%作为训练集，其余作为测试集。然后，使用训练集训练DBN，完成特征提取。再将DBN的权重(W′)和偏值(b′)初始化DNN对应层的权重(W)和偏值(b)，通过DNN进行目标值预测，并微调参数提高模型性能。最后，使用测试集测试预测模型的准确度和适用性。图1中：In表示输入层，h1表示第1层隐藏层，hn-1表示第n-1隐含层，hn表示第n层隐含层。

2.1 数据集归一化

数据归一化是将数据集按比例缩放，使之落入一个小的特定区间，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够比较和加权。一方面可以加快模型收敛速度，另一方面让各个特征对结果做出相同的贡献，提升模型的精度。采用式(6)所示的最大最小归一化方法，将原始数据集进行线性变化，使结果落到[0,1]区间，若原始订单特征数据均相同，则代表各特征贡献相同，用1表示。

(6)

式中Xmax和Xmin表示原始数据集中对应特征的最大值和最小值。

2.2 基于DBN特征提取

DBN由若干个受限玻尔兹曼机(Restricted Boltzmann Machine, RBM)堆叠组成，一个RBM由一层可见层和一层隐含层构成，可见层和隐含层的神经元之间为双向全连接[22]。DBN一方面在降低特征数据维度时，尽可能保留了原始特征；另一方面在训练神经网络时，难免会出现过拟合现象，DBN能够有效改善这个问题。

假设某个RBM可见层有V个神经元，隐含层有H个神经元，对给定状态(v,h)，能量函数定义如式(7)所示[23-24]：

(7)

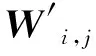
基于以上能量函数，给定状态(v,h)的联合概率分布如式(8)所示：

(8)

式中Zθ表示配分函数。

由于RBM层间相互连接、层内不连接的特殊结构，当给定可见层各神经元的状态时，隐含层各神经元的激活状态是相互独立的。同理，当给定隐含层各神经元的状态时，可见层各神经元的激活状态也相互独立，因此第j个隐含层神经元和第i个可见层神经元的激活概率分别如式(9)和式(10)所示：

(9)

(10)

其中σ表示激活函数。

传统的激活函数有Sigmiod函数和Tanh函数，但两者的导数值都在(0,1)范围内，当进行多层反向传播时，误差梯度会不断衰减，容易出现梯度消失，模型学习效率较低，同时还会丢失数据中的一些信息。本文采用ReLU激活函数[25]训练RBM，一方面能克服梯度消失，极大可能的保留数据信息；另一方面该激活函数会使一些输出为0，使网络具有稀疏性，缓解过拟合问题。

由于分配函数Zθ难以计算，导致联合概率分布Pθ(v,h)无法计算。2002年，Hinton等[26]提出对比散度(Contrastive Divergence, CD)算法，以加快RBM训练学习。通过CD算法对RBM进行训练，各个参数更新规则如式(11)～式(13)所示：

W′=W′+ρ(hvT-h′(v′)T)，

(11)

b′=b′+ρ(h-h′)，

(12)

a′=a′+ρ(v-v′)。

(13)

式中:v′表示可视层v的重构，h′表示根据重构v′所得隐藏层，ρ表示学习效率。

2.3 基于DNN订单完工期预测

DBN预训练通过学习输入数据特征的耦合关系完成特征提取，为DNN训练提供合理的初始参数。如图1所示，在DBN完成预训练之后，将DBN参数作为DNN对应层的初始参数，DNN最后一层网络参数随机给定，与其他层不同，该层的主要任务是利用前面网络提取的特征完成订单完工期预测。在训练过程中，预测值和实际值有一定的差距，因此使用BP算法对网络参数进行微调，提高预测的准确度。本文采用的是对整个网络的参数进行调优，提高网络预测性能，摆脱只对最后一层网络参数调整而陷入局部最优解的困境。

在训练神经网络的过程中，经常会发生过拟合现象，这导致网络在训练集上的表现力极强，而在测试集上的表现力较弱。由奥卡姆剃刀定律[27]可知，模型越复杂，越容易过拟合。为了降低DNN的复杂度，改善DNN的过拟合现象，加入dropout和L2正则化：

(1)dropout是在深度学习网络的训练过程中，将神经网络的神经元按照一定的概率将其短暂性地从网络中丢失[28]。dropout一方面简化神经网络结构，能够减少训练时间；另一方面每个神经元都以一定的概率出现，不能保证相同两个神经元每次都同时出现，权值更新不再依赖于固定关系神经元的共同作用，从而改善DNN的过拟合现象。

(2)L2正则化的思想是在原始损失函数Loss0的基础上加一个正则项，即各层权重Wk的平方和，使在显著减少目标值方向上的参数保留相对完好，对无助于目标值方向上的参数在训练过程中因正则项而衰减。具体形式如式(14)所示：

(14)

3 实例分析

根据上述特征数据集，通过反复试验，最终选择相对较好的DBN-DNN网络结构及参数进行订单完工期预测。DBN网络结构如下：1059→750→300→50，参数设置如下：学习率α=0.000 1，批尺寸batch_size=128，学习周期epochs=20。设计DNN网络结构如下：1 059→750→300→50，参数设置如下：学习率α′=0.001，dropout数据特征保留概率keep_prob′=0.9，批尺寸batch_size′=128，学习周期epochs′=150。因为均方根误差(RMSE)对预测中特大或特小误差非常敏感，所以RMSE能够很好的反映预测模型的准确度。RMSE是指预测值与真实值偏差的平方与预测次数(m′)比值的平方根，计算如式(15)所示：

(15)

将使用Sigmoid激活函数训练DBN，并在DNN中未添加dropout和L2正则化的预测模型称为R-DBN-DNN。图2是本文设计的预测模型和R-DBN-DNN在同样参数条件下的求解结果，实线表示训练集的优化过程，虚线表示测试集的测试过程。从收敛速度看，前者以较快的速度收敛；从模型泛化能力看，前者在训练集和测试集上的最小RMSE分别为17.11和21.22，后者在训练集和测试集上的RMSE分为别8.01和31.81，虽然后者在训练集上误差小，但在测试集上误差远大于前者。

预测模型完成训练后，将测试集输入模型，验证模型的准确度。预测结果如图3所示，描述的是从测试集中选取200个样本(sp200)作为预测对象，实线表示样本的真实值，虚线表示模型的预测值，可以看出预测值与真实值非常接近，且两者的变化方向和幅度几乎相同。

用模型预测值与样本真实值之间的差值大小评估预测模型的好坏。本文使用RMSE、残差平方和(SSE，计算如式(16))、平均绝对误差(MAE,计算如式(17))、R平方(R2,计算如式(18))和预测时间(T)评价预测模型在测试集上的预测性能。

(16)

(17)

(18)

神经网络[20]和支持向量回归[9]被广泛运用于订单完工期预测或相似目标预测，为阐述本文所提方法的准确度和适用性，提出以下3种方法进行对比分析，通过反复实验得到相对较好的训练参数：

(1)使用多隐含层的基于误差逆传播算法的BP神经网络进行预测，该模型的结构为1 059→750→300→50→1，与本文设计的模型结构相同，参数设置如下：学习率α=0.001，dropout数据特征保留概率keep_prob=0.82，批尺寸batch_size=256，学习周期epochs=150，该方法简称为M-BPNN。

(2)首先使用主成分分析(PCA)方法将数据集从1 059个特征降维到300个特征，然后使用BP神经网络进行预测，该网络结构为300→50→1，参数设置如下：学习率α=0.001，dropout数据特征保留概率keep_prob=0.85，批尺寸batch_size=128，学习周期epochs=150，该方法简称为PCA-BPNN。

(3)首先使用PCA方法降维至100个特征，然后基于支持向量机的回归算法SVR进行预测，选择径向基核函数，核函数系数gamma=0.01，惩罚因子C=100，该方法简称为PCA-SVR。

不同比对模型对sp200预测结果如图4所示，不同模型对测试集预测精度统计分析结果如表1所示。从图3和图4可以看出，与其他3种预测模型相比，DBN-DNN的样本实际值(实线)和样本预测值(虚线)拟合程度最好，表明其预测精度最高，PAC-BPNN实线与虚线偏差最大，预测结果出现了最大误差；车间存在随机扰动，在M-BPNN、PCA-BPNN、PCA-SVR三种预测模型中，少部分样本实际值与预测值相差较大，而DBN-DNN每个样本预测值都比较精确，抗干扰能力较强。在训练过程中，与DBN-DNN相比，M-BPNN损失值波动较大，增大批尺寸，梯度下降方向更准确，且容易陷入过拟合，减小dropout特征保留概率，提高泛化能力。表1通过描述模型好坏的评价指标：RMSE、SSE、MAE、R2，以数值形式直观地验证了DBN-DNN优于其他3种预测模型。这4种预测模型预测精度从高到低分别是：DBN-DNN,M-BPNN,PCA-SVR,PCA-BPNN，验证了DBN-DNN在解决预测问题的最优性。

表1 不同回归算法结果对比

从本实验可以得到以下结论：

(1)与R-DBN-DNN相比，ReLU激活函数避免了梯度消失，以较快的速度收敛于最小值，并使网络具有稀疏性，与dropout、L2正则化共同改善了DBN-DNN预测模型的过拟合问题，提高了模型的泛化能力。

(2)与M-BPNN相比，DBN确定的DNN初始参数优于M-BPNN模型随机生成的初始参数，不易收敛到局部最优解。

(3)与PCA-BPNN和PCA-SVR相比，DBN-DNN的特征提取、逻辑推理能力强，更适合处理大量的生产制造数据。

(4)在以上所有预测模型中，DBN-DNN的可靠性、适用性强，预测值最接近真实值，拟合复杂制造系统非线性映射程度最高。

4 结束语

本文重点针对复杂制造系统订单完工期预测展开研究，建立了一种基于DBN-DNN的离散制造车间订单完工期预测模型。该方法采用ReLU激活函数改进特征提取模型，极大可能地保留了数据信息；在回归预测模型中，增加dropout和L2正则化，改善了模型过拟合现象，提高了模型的泛化能力。

将基于DBN-DNN的订单完工期预测模型运用到某航天机加车间中，随着订单完工期预测能力的提升，车间生产计划更加合理，调度排产更加科学，提高了车间整体运行效率。在后续的研究中可以考虑车间的突发状况数据，提高模型的鲁棒性，并通过建立大数据分布式处理平台，提高计算效率。