可反馈线性化系统的鲁棒自适应容错控制设计
姚雪莲,杨 艺
(江苏理工学院汽车与交通工程学院,江苏常州 213001)
1 引言
执行器故障是性能关键系统中的一种常见的故障类型,该故障的发生会引起严重的性能损失甚至造成系统不稳定从而引发灾难性的事故.执行器故障的具有多重本质不确定性,即故障模式、故障发生时间、故障值大小以及故障类型都是未知的.因此需要发展有效的容错控制技术以补偿不确定执行器故障对系统性能的影响,从而确保闭环系统的可靠性和安全性.近年来,执行器故障补偿控制问题已经引起了越来越多研究者的关注,尝试了多种控制方法,并取得了一些成果.文献[1–4]综述了多种有效的容错控制方法.文献[5–6]将多模型自适应控制方法用于故障补偿设计中.文献[7–9]将神经网络用于传感器或执行器故障情况下可重构飞行器控制设计中.文献[10]基于自适应滑模控制方法设计近空间飞行器的故障辨识和容错控制策略.文献[11]针对含有外界扰动的航天器姿态控制系统,提出两种有效的容错控制方法.为提高多传感器测量系统的整体性能及减小各个传感器故障对系统造成的影响,文献[12]提出了一种新的多传感器信息融合设计框架.故障检测和诊断方法也被广泛用于解决被控系统的元部件故障问题[13].文献[14–15]将自适应观测器设计用于重构执行器故障,基于故障估计信息设计容错控制器.除上述容错控制方法外,自适应控制也是一种有效的工具被广泛的用于线性系统和非线性系统的容错控制设计中[16–18].尽管非线性系统的执行器故障补偿控制研究取得了大量可行的进展,但对含有不确定动态和执行器故障的被控系统而言,仍有许多值得深入研究的开放性问题,如针对一般的非线性系统,研究其多重执行器故障补偿控制问题,从而实现闭环系统稳定和渐近输出跟踪的控制目标.所谓的可反馈线性化系统,指的是一类可以通过合适的非线性反馈控制将其线性化的非线性系统[19].在反馈线性化设计的基础上,可以进一步实现模型匹配、极点配置或跟踪等控制目标.文献[20]和文献[21]将反馈线性化理论与自适应控制相结合设计能够有效解决非线性系统的参数不确定和容错控制问题.此外,非线性控制系统实际运行环境中存在各种扰动,使得被控系统的性能受到不同程度的影响,因此在控制器设计过程中应考虑扰动抑制问题.文献[22–24]针对线性系统中可测量干扰,可通过干扰解耦的方式解决干扰抑制问题,然而该方法不适用于不可测量干扰的抑制问题.文献[25–26]针对不可测量干扰提出鲁棒控制方法,然而无法实现渐近跟踪的控制目标.基于自适应控制设计的干扰抑制方法能够有效估计未知的系统参数和干扰参数.文献[27]将自适应内模控制方法用于解决航天器系统中,实现其在外界干扰环境下的姿态跟踪.针对含有不确定系统参数和外界干扰的通用高超声速飞行器,文献[28]提出一种新的滑模控制方法.文献[29]解决正弦干扰下非线性系统的渐近跟踪问题,所设计的干扰抑制算法主要是针对单输入单输出非线性系统,不适用于含有不匹配干扰的多输入多输出非线性系统.此外,文献[30–31]研究了多输入多输出非线性系统不匹配干扰的抑制问题.
实际运行环境中可能同时发生未知干扰和不确定执行器故障,该情况下多输入多输出非线性系统的渐近跟踪控制设计变得更具有挑战性.尽管针对多输入多输出非线性系统的干扰抑制和执行器故障补偿问题已经取得了一定的理论研究成果,仍存在一些重要的开放性的问题值得研究.本文针对一类可反馈线性化的多变量非线性系统,进一步研究多重不确定执行器故障补偿和不匹配输入扰动抑制问题.与现有的一些容错控制方法相比,本文提出的控制方法有以下几个特点:1)相比于部分文献中研究对象为一类标准型非线性系统,本文所研究的多变量非线性系统更具有一般性;2)提出一种新的非切换式的综合容错控制方法,该方法融合多个能够解决某具体故障模式下的故障补偿设计,得到一个能够处理多故障模式的综合控制器;3)针对控制输入关于系统的相对阶与干扰关于系统的相对阶之间的关系,设计多变量非线性系统的不匹配干扰抑制策略;4)详细讨论系统输入和扰动关于系统输出的相对阶之间的关系,分别给出不同的鲁棒控制器设计思路.
2 问题描述
本章描述含有冗余执行器系统的执行器故障补偿和扰动抑制问题.考虑如下非线性系统:

控制目标.本文针对可能发生至多一个不确定执行器故障(2)和不匹配外界扰动d(t)的可反馈线性化非线性系统(1),设计自适应控制器v(t)解决故障和扰动的多重不确定性,从而保证闭环系统稳定且系统输出y(t)渐近跟踪给定的参考输出.
故障模式.定义σ(t)=diag{σ1(t),σ2(t),···,σm(t)}为执行器故障模式矩阵.如果第j个执行器发生故障则σj(t)=1,否则σj(t)=0.当系统发生不确定执行器故障时,系统上的实际输入量u(t)可以表示为

3 外界干扰抑制设计
本章先基于反馈线性化设计得到基础控制器,然后构建因未知干扰参数引起的状态误差动态方程并设计自适应干扰抑制控制器,保证无故障情况下闭环系统稳定和渐近输出跟踪.
3.1 反馈线性化
多输入多输出非线性系统:

基于假设1,当非线性系统(1)的系统参数和故障参数均已知的情况下可以应用反馈线性化设计设计得到一个理想的控制器.通过对系统(1)中yi进行ρi次求导,可以得到


3.2 自适应干扰抑制
本节针对ρi与νi不同大小关系,分别讨论外界扰动抑制设计.
3.2.1 ρi <νi情况下扰动抑制设计
如果ρi<νi, ii1,i2,···,iP,该情况下外界干扰对系统输出没有影响,则δi(x,t)=0.式(8)可以进一步表示成以下形式:

当m=q,且G(x)满足行满秩的条件,设计控制输入信号为

从而得到线性化系统
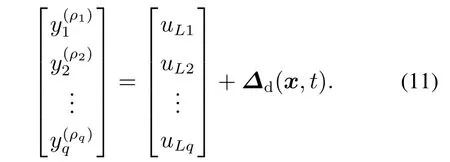
设置uLi(i=1,2,···,q)为

选取αiρi,i=1,2,···,q,式(12)使得输出误差及误差的高阶导数ei,,···,随着t趋于无穷而渐近趋近于零.
3.2.2 ρi=νi情况下扰动抑制设计

从而得到线性化系统


系统能够获得期望的性能.
3.2.3 ρi >νi情况下扰动抑制设计
若ρi>νi, i ∈{1,2,···,m},则式(8)可以表示为
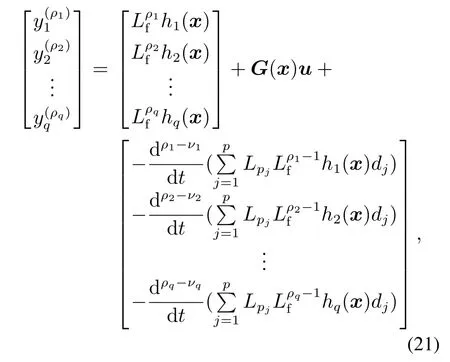
其中δi(x,t)与干扰d(t)以及干扰微分项,···,dρi−νi(t)相关.在该情况下,为实现干扰抑制和渐近输出跟踪控制,需事先获取干扰的微分信息且十分复杂,故在本设计中不考虑此类情况.
4 执行器故障补偿设计
本章节首先针对可严格反馈线性化的非线性系统结合控制等式
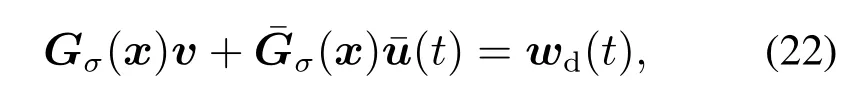
从而设计故障补偿控制器,其中:Gσ(x)=G(x)σ,

根据ρi和νi的不同关系得到uL为式(15)或式(17),其设计过程包含自适应控制器、误差等式、参数自适应更新律和稳定性分析,然后将故障补偿控制算法推广至部分反馈线性化系统.
4.1 严格反馈线性化系统的故障补偿设计
在执行器故障(6)下,系统模型可以表示为

若系统(1)相关度{ρ1ρ2··· ρq}满足ρ1+ρ2+···+ρq=n,则不确定执行器故障情况下该系统可被严格反馈线性化并转化为
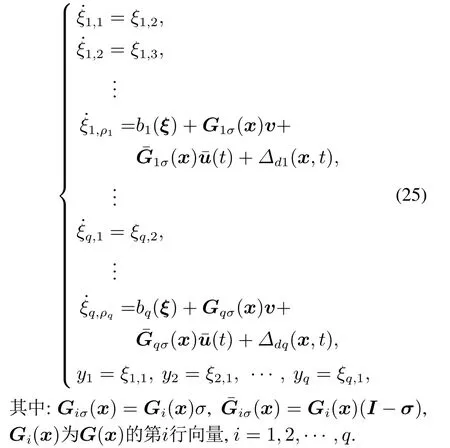
当系统发生不确定执行器故障的情况下,通过求解式(22)得到对应故障情况下的控制输入信号v(t).假设故障信息(故障模式、故障值与故障时间)已知,针对无故障和执行器u1故障两种情况分别设计理想的控制器

自适应控制器结构.由式(30)可以推导出自适应控制器的结构为


注1为演示本文的干扰抑制和故障补偿设计过程,本文仅考虑至多一个执行器故障情况.此外本文所提的算法能够扩展用于解决多个执行器故障情况下的扰动抑制和故障补偿问题,以m=6,q=3为例,简述u1,u3和u5同时发生故障的控制器设计过程.

故障补偿设计的其他过程(包括自适应控制律v(3)(t)的参数化设计、参数信号的自适应律以及性能分析)与本文第4.1节相似.从上述设计过程可以得出:本文所提的自适应干扰和故障补偿设计同样适用于解决多个执行器同时故障情况下非线性系统的控制问题并获得期望的系统性能.
综上所述,可以得到以下定理.
定理1针对可能发生不确定执行器故障(2)和不匹配干扰d(t)的多变量非线性系统(1),若ρ1+ρ2+···+ρq=n且不确定故障情况下的等效控制矩阵Gσ(x)=G(x)(I −σ(t))在域U(定义为h:U ⊂Rn→V ⊂Rq)内行满秩,控制器(31)及其参数自适应律(34)–(36),能够保证闭环系统稳定和渐近输出跟踪:
4.2 部分反馈线性化系统的故障补偿设计
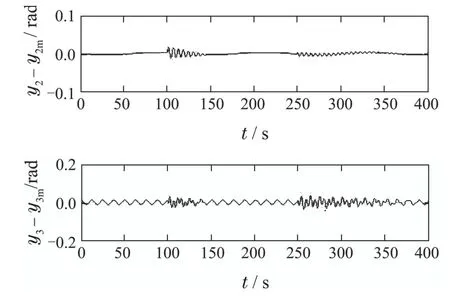
若ρ1+ρ2+···+ρq 及零动态子系统 与σ有关. 为保证闭环系统稳定和系统输出yi(t)渐近跟踪参考信号ymi(t)(其中ymi(t)的ρi,i=1,2,···,q微分有界且分段连续),本文将基于以下假设条件进行控制器设计: 假设2本文考虑的故障模式集中任意故障情况下,非线性系统(1)仍为最小相位系统,即在(t),d(t)和ξ输入作用下,零动态子系统:=ψ(ξ,η)+)为输入状态稳定. 结合假设条件1,针对部分反馈线性化系统所设计的自适应故障补偿控制信号v(t)与第4.1节中针对完全反馈线性化系统相似,这里不再赘述.基于零动态的输入状态稳定条件(假设条件2)且不确定故障情况下的等效控制矩阵Gσ(x)在域U内行满秩,自适应控制器(31)及其参数自适应律(34)–(36)能够保证系统(1)在发生多重不确定执行器故障(2)和未知干扰情况下闭环系统稳定和渐近输出跟踪. 本节将所提出的控制方法应用于飞行器的飞行控制系统中,仿真结果表明该方法能够有效解决阵风扰动下飞行器的不确定执行器故障补偿问题. 文献[33]中关于湍流条件下飞行器动态模型研究表明,飞行器的纵向非线性动态模型可以表示为[34] 其中:V 为飞行器速度,α为攻角,θ为俯仰角,q为俯仰角速率,m为质量,Iy为转动惯量,M为俯仰力矩,d1,d2和d3为湍流扰动信号, 控制目标.针对含有不确定湍流干扰和执行器故障的飞行器控制系统(45),设计自适应故障补偿控制器保证闭环系统稳定,且系统输出y(t)=[V α θ]T跟踪期望的控制指令 根据假设1 可以得到ρ1=v1=1,ρ2=v2=1,ρ3=v3=2,ρ1+ρ2+ρ3=4.系统满足假设条件2且反馈线性化后不含零动态子系统.经验证diag{1,0,0,0},diag{0,0,0,1},diag{0,0,0,0}均符合故障补偿要求,故通过该3种故障情况验证算法的有效性. 飞行器参数见文献[35],干扰参数为 仿真验证中,考虑以下故障情况:i)当t<100 s,系统无故障情况:ui(t)=vi(t), i=1,2,3,4;ii)当100 s 初始状态: 干扰模型基函数: 初始干扰参数: 仿真结果如图1至图3所示,其中图1为系统实际输出及对应的参考信号之间的一个对比关系,图2为系统的跟踪误差,图3为飞行器中4个执行器作用于系统的控制输入信号. 图1 系统输出与参考输出信号Fig.1 System outputs and reference outputs 图2 跟踪误差Fig.2 Tracking errors 图3 控制输入信号Fig.3 Control inputs 从图1和图2可以看出实际运行过程中无论是正常运行还是不确定故障情况下(如图3所示,当t=100s执行器u1故障,t=250 s执行器u4故障),所设计的控制算法始终能够实现闭环系统稳定且渐近输出跟踪的控制目标.图1表明t ∈[0,100 s)时间段内,系统存在外界干扰无执行器故障,系统输出跟踪给定指令过程中出现瞬态响应,并且随着时间变化瞬态响应逐渐减小,从而验证本文所设计的控制方法具有鲁棒性.仿真结果验证了本文自适应执行器故障和干扰补偿算法的有效性. 针对一类含有多重不确定执行器故障和不匹配输入扰动的多变量非线性系统,本文基于反馈线性化设计提出一种自适应执行器故障和干扰补偿控制方法.自适应干扰补偿设计的关键指出在于确定控制输入关于输出的相对阶与干扰输入关于输出的相对阶之间的关系.执行器故障具有多重不确定性,尤其故障模式和故障值参数不确定.本文采用自适应算法对其进行估计并基于参数估计构建自适应故障补偿控制器集合,然后采用加权算法将多个控制器融合成一个综合控制器,从而解决多重不确定执行器故障情况并能够保证闭环系统获得期望的性能.故障和扰动情况下飞行器的仿真控制研究结果验证了方法的有效性.

5 仿真研究
5.1 湍流情况下飞行器动态



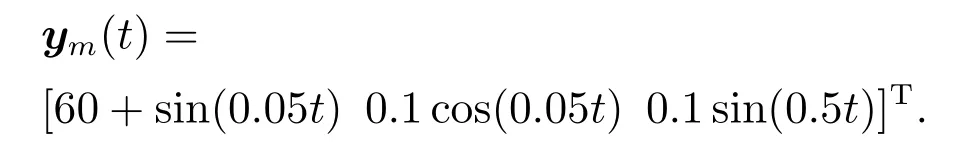
5.2 仿真条件

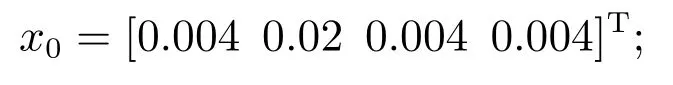
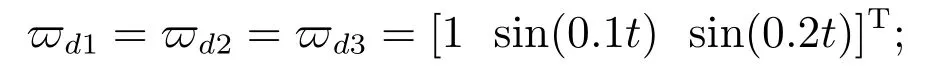

5.3 仿真结果



6 结论

