基于卷积网络与支持向量机的云资源预测模型

杨 云,闫振国

(陕西科技大学 电子信息与人工智能学院,陕西 西安 710021)

0 引言

云原生容器技术的生态系统正在快速发展，以Kubernetes为代表的容器云成为新的分布式架构解决方案.容器云封装整个软件运行时环境，为开发者提供用于构建、发布和运行分布式应用的平台[1].云资源的调度管理与部署是影响系统性能的重要因素.资源供应不足会导致服务水平协议(Service-Level Agreement,SLA)违约和服务质量(Quality of Service,Qos)下降，而过度供应又会带来资源浪费，增加网络、冷却和维护成本[2].高效的资源管理需要与应用需求动态贴合.但是新资源从请求、调度、部署到启动存在一定的时间延迟，这意味着，当系统达到某个负载阈值才请求新资源的反应性技术，在业务繁忙期会增大系统运行压力.而应对高流量的临时系统扩容又是必不可少的，包括系统规格扩增、服务扩展以及后端扩容.所以在系统过载之前预测未来时间窗口的云资源请求，提前进行调度分配与编排部署是应对该问题的有效解决办法.

云资源需求的波动不是一个随机游走过程，而是前后关联的.其相似的形态模式随业务规律会差异性复现.因为云资源序列与时间的高度相关，现有研究将其作为时序问题开展分析.针对云资源预测，早期的方法有基于统计学的自回归移动平均法(ARIMA)[3]、指数平滑法[4]等.ARIMA要求时序数据经过差分化之后是稳定的，本质上只能捕捉线性关系.指数平滑法对数据进行非等权处理，给予近期数据较大权值，但对转折点缺乏鉴别能力，长期效果较差.后来传统机器学习方法得到了广泛发展，Zia等[5]利用自回归神经网络(AR-NN)组合模型预测实时资源使用情况；Jitendra Kumar等[6]提出神经网络与自适应差分进化的结合方法，在精度上优于反向传播网络；Gopal等[7]利用贝叶斯模型预测内存密集型应用的资源需求.赵莉[8]采用支持向量机(Support Vector Machine,SVM)结合混沌分析方法对云资源序列进行处理，仿真实验对比神经网络大幅提高了预测精度；Wei等[9]将小波变换与支持向量机的优点结合，提出一种基于加权小波支持向量机的云负载预测模型，为不同样本赋予不同等级权重，同时利用改进的粒子群算法优化参数组合，进一步提升了预测效率.以上模型中神经网络具备良好的非线性映射能力，但随复杂度的提高阈值和权重参数成倍增加，训练结果容易过拟合或陷入局部最优，贝叶斯模型只适合特定预测场景.而相比其他学习算法，支持向量机同时考虑经验风险和结构风险最小化，使用核方法进行非线性学习，其作为二次凸优化问题同时避免了神经网络的局部最优缺陷，取得了更为理想的效果.

随着深度学习在时序预测领域的发展[10]，研究者开始利用卷积神经网络(Convolutional Neural Networks,CNN)、循环神经网络(Recurrent Neural Network,RNN)及其变体长短时记忆网络(Long Short-Term Memory,LSTM)等深度模型对序列进行处理.Yonghua Zhu等[11]使用循环神经网络提出基于注意力机制的LSTM云负载预测方法；Omer等[12]使用卷积神经网络(CNN)将时间序列转换为二维图像，根据原始时间序列起伏标注图像特征；Alberto Mozo等[13]利用CNN预测本地数据中心网络流量负载的短期变化，证实了CNN可以捕捉具有高度非线性规律的TCP连接数量；S Chan 等[14]使用CNN-SVM的混合建模技术对非平稳的多元时间序列进行了短期负荷预测，相比传统时序方法在精度上取得了显著优势.

在云场景中，资源需求波动是一个逐渐演变的过程，存在时间维上局部相关性的同时，受到空间维拓扑结构的影响，各结点的负载波动会链式带动其他结点的计算资源管理弹性变化[15].例如Kubernetes云平台依据服务发布Pod的负载情况动态调整外部存储对于业务的扩缩容响应.卷积神经网络并行化效率高，结构稳定，能够从局部特征关联聚合得到整体，从各维度挖掘潜在模式，相比其他方法更能满足云场景的时空维建模需求.现有方法中，通常使用单一预测模型或者是使用组合模型对不同预测结果进行权重集成，虽然有一定性能提升，但并未根本解决较差模型的短板影响.基于此，本文提出一种使用卷积网络与支持向量机相结合的预测算法，将卷积网络的特征学习能力与支持向量机的回归拟合能力结合，利用图卷积建模拓扑结构的空间维特征，同时利用遗传算法改善支持向量机的参数优化.从特征建模与拟合回归两方面提升现有方法预测能力.

1 问题定义

定义1(拓扑映射)容器云平台应用集群的资源负载随业务逻辑调用及时序演变呈非线性动态变化，将结点间的拓扑关联映射为图结构数据，用无向图G=(V,E)表示，V是结点集，结点个数|V|=N，E为边集，代表结点间拓扑连接.

定义2(时序数据)结点监测M个云资源指标(包含CPU、Memory等)的时间序列数据，即结点在特定时间切片产生M维特征向量.用三元组

x(v,m,τ)表示结点v的m维指标在时刻τ的监测记录，其中v为结点标识，m∈M为特征标识，τ为时间标识.用t=[tstart,tend)表示某个时间区间，Δt=tend-tstart为区间长度，则在t时段内，所有结点的第m维指标监测序列记录表示为张量Xm=

|{x(v,m,τ)|x.v∈N∧x.m=m∧x.τ∈t}|.用

Xτ=|{x(v,m,τ)|x.v∈N∧x.m∈M∧x.τ=τ}|

表示所有结点的所有监测指标在时刻τ的记录值.

定义3(滑动窗口)利用滑动窗口采集历史时间序列记录，将moveGAP[tstart,Δt]=Xm(tstart为起始记录,Δt为窗口长度)称为m维指标的Δt滑动采集窗口.

定义4(问题定义)本文的预测任务为，依据应用集群历史时序片段的资源使用记录值，预测未来时间窗口TP的资源使用需求.记当前时刻为t0，用X=(Xt0-Th+1,Xt0-Th+2,…,Xt0)∈Th×N×M表示所有结点在历史区间Th的记录值，用Y=(Xt0+1,Xt0+2,…,Xt0+Tp)∈Tp×N×M表示所有结点在未来区间Tp的待预测值，则本文的目标是学习如公式(1)所示的映射模型f(·).

(Xt0+1,Xt0+2,…,Xt0+Tp)

(1)

数据准备：云资源时序数据的待预测时段随集群业务负载变化而与其近期、日周期、周周期片段产生关联，滑动窗口依据规律特性从三个维度采集序列数据.假设结点监测的采样频率为每天l次，用χr表示从近期片段采集的时序数据，即与预测窗口直接相邻的时序片段，则有χr=moveGAP[tstart,Δt](tstart=t0-Tr)，其中Δt=Tr为近期片段长度；用χd表示按日周期规律采集的时序数据，即与预测窗口相邻日期的同时段数据，则有χd=moveGAP[tstart,Δt](tstart=t0-(Td/Tp)×l,t0-(Td/Tp-1)×l,…,t0-l)，其中Δt=Tp，Td为日周期片段总长，采集步长为l；用χw表示按周周期规律采集的时序数据，即在预测窗口相邻周内同星期且同时段属性的数据，则有χw=moveGAP[tstart,Δt](tstart=t0-(Tw/Tp)×7×l,t0-(Tw/Tp-1)×7×l,…,t0-7×l),其中Δt=Tp,Tw为周周期片段总长，采集步长为7×l.Tr、Td及Tw均为预测窗口Tp的整数倍.将三个维度的采集片段作为原始输入，确保模型充分捕获时间维特征.则模型的输入数据X及历史区间Th可由公式(2)、(3)表示.

Th=Tr+Td+Tw

(2)

X=[χr,χd,χw]∈Th×N×M

(3)

2 卷积网络与支持向量机模型

2.1 卷积网络

本文通过图卷积建模云资源拓扑结构的空间维特征，刻画邻近结点的信息聚合，再沿时间轴卷积，捕获序列数据的时间维依赖，通过多个图卷积与时间维卷积的堆叠网络学习特征表示.

现有的图卷积神经网络主要有两类:谱图方法和空间方法.本文通过谱图方法在谱域定义图卷积.谱图方法概括说就是利用图的拉普拉斯矩阵的特征值和特征向量研究图的性质，通过对谱空间的信号做傅里叶变换实现卷积操作，而傅里叶变换的定义依赖于拉普拉斯矩阵[16].无向图G的拉普拉斯矩阵的一般定义为L=D-A，其中D是顶点的度矩阵，为对角矩阵，对角线上的元素依次为各个顶点的度，A是邻接矩阵.

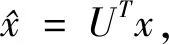
gθ*Gx=gθ(L)x=gθ(UΛUT)x=

Ugθ(Λ)UTx

(4)

youtput=σ(Ugθ(Λ)UTx)

(5)

其中，gθ(Λ)=diag([Θ0,…,ΘN-1])，卷积核参数通过初始化赋值然后利用反向传播进行调整.因为非线性变换在非欧空间数据的图结构中作用有限，使得图卷积操作发挥作用的是每一层的特征传播机制[18]，所以本文放弃层之间的非线性变换，即将特征传播融合到一个层内，进行维度变换后再由激活函数作用在聚合结果上.σ(·)是激活函数，本文使用线性修正单元ReLU.youtput即为卷积层输出，刻画邻近节点的信息聚合.但是由于每一次前向传播都要进行谱分解及计算大规模的矩阵乘积，代价较高，所以本文采用切比雪夫多项式进行近似求解[17]：

(6)

gθ*Gx≈

θ0x+θ1(L-IN)x+θ2(2(L-IN)2-IN)x

(7)

简化计算以K=2为例，卷积操作表示为：

gθ*Gx≈θ0x+θ1(L-IN)x=

(8)

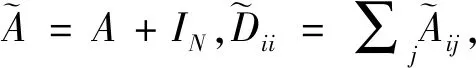
(9)

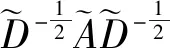
经过图卷积建立结点数据间的空间相关性，再由标准卷积提取隐藏的时间维特征信息，组成一个时间图卷积模块，由多个时间图卷积结构堆叠形成卷积网络层，如图1所示.

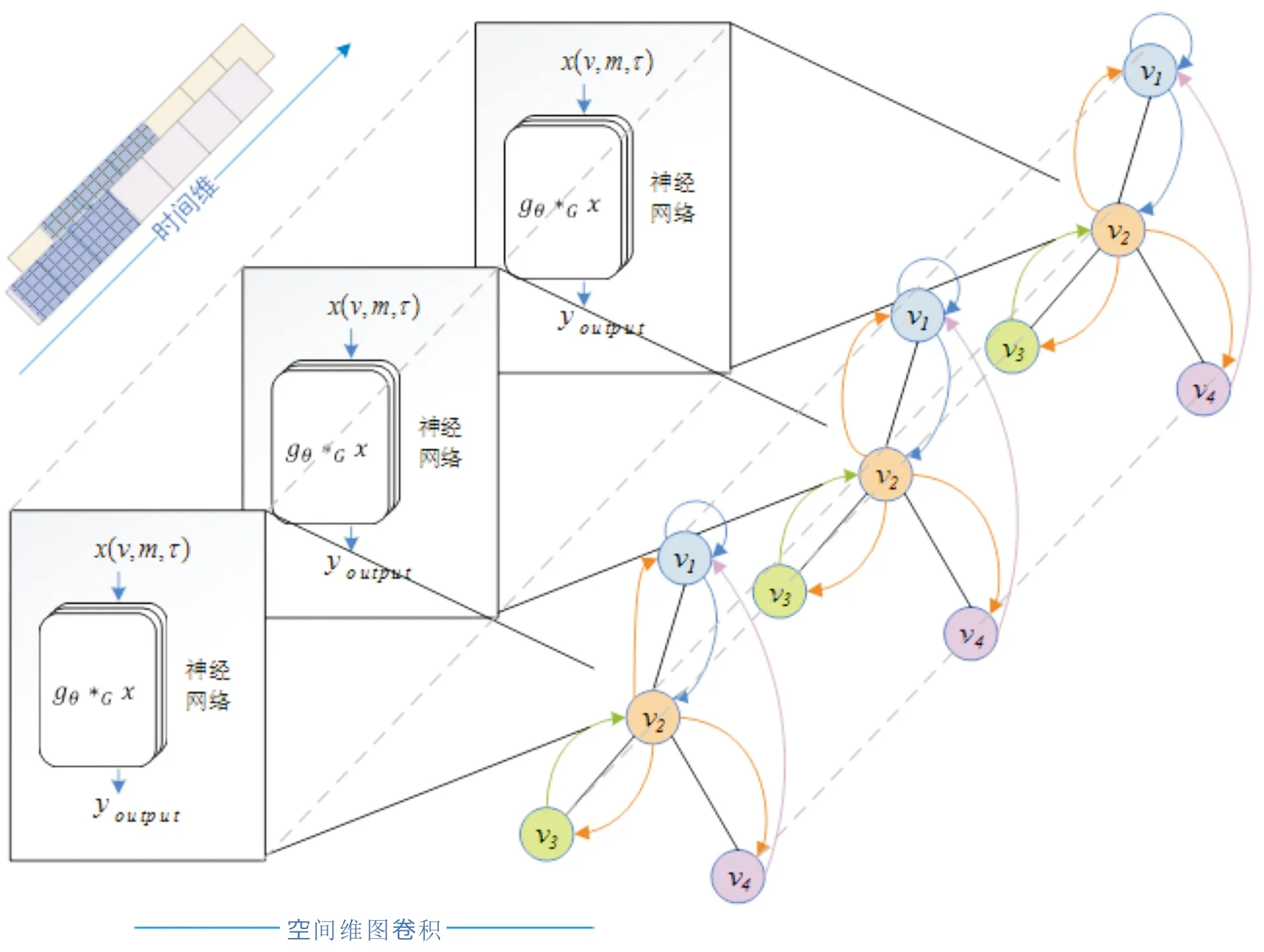
图1 时间图卷积结构

以x∈N×Hi×Ti代表一层时间图卷积模块的输入，Hi代表结点的输入特征维度，Ti为输入时间维长度，用N×Ho×To表示该层时间图卷积的输出，也即为下一层的输入，Ho与To分别为输出特征维度与时间维长度，则一个时间图卷积模块的形式化定义为：

(10)

其中,σ(·)是时间维卷积单元的激活函数，本文使用修正线性单元ReLU.Γ*为时间维卷积操作.gθ∈K×Hi×Ho为待学习的图卷积核参数.结点特征由Hi维转化到Ho维.时间维卷积示意图如图2所示.使用训练好的时间图卷积模型对原始输入数据进行特征提取，进行维度转换后从全连接层提取特征数据输入支持向量回归机(Support Vector Regression,SVR)完成回归训练.

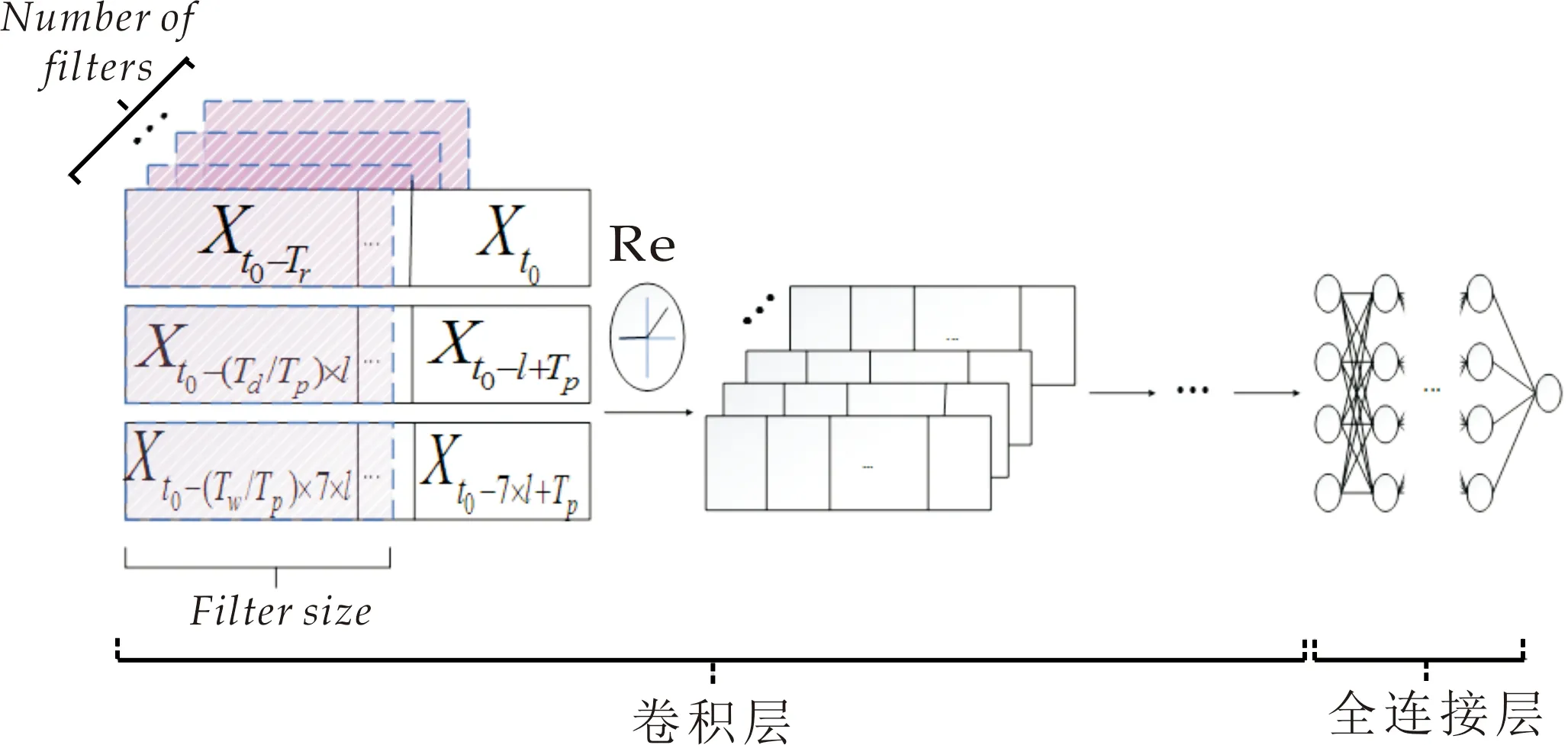
图2 时间维卷积示意图

2.2 支持向量回归

将经过多层时间图卷积获得的特征向量送入支持向量回归机(SVR)训练，在过拟合时利用主成分分析降低特征向量维数.实验中发现特征提取相比SVR调参对预测结果的影响更大，而时间图卷积模块确保了特征提取不会成为提高准确率的瓶颈.

(11)

s.t.ω·φ(xi)+bi-yi≤+ξi,

yi-(ω·φ(xi)+bi)≤

ω,b是待确定的目标模型参数，分别为回归模型中的权重向量与偏置量，φ(x)为映射函数，C为正则化常数，对结构风险和经验风险进行折中，

ω·φ(xi)+bi为模型估计，yi为真实输出.面对该类二次规划问题，通过引入拉格朗日乘子求得上式对应拉格朗日函数，继而代入模型参数与松弛变量的偏导等式得其对偶问题，依据Karush-Kuhn-Tucker条件，解得拉格朗日乘子，即可通过下式解得模型偏置量b,可取多个样本得其平均值：

b*=yi+

(12)

κ(x,xi)=μκRBF(x,xi)+(1-μ)κPOLY(x,xi)

(13)

(14)

κPOLY(x,xi)=(xTxi)d

(15)

其中，μ为权值系数，d≥1为多项式次数，ρ为带宽.SVR的决策回归函数为:

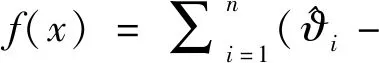
(16)

参数的选择对模型的预测精准度与泛化能力有着重要影响，相对于文献[8]的主观取参方式,本文结合云资源序列的非线性与复杂性特点，利用遗传算法(Genetic Algorithm,GA)进行参数寻优.

GA寻优的SVR参数包括：惩罚参数C、核函数系数ρ、多项式核最高次项次数d、核函数组合权值系数μ.算法步骤描述如下：

(1)初始化种群.随机生成初始群体，以C、ρ、d、μ参数作为基因构建n个染色体，采用多参数级联拼接方式，惩罚参数C和核函数带宽ρ使用间接二进制编码，去除小数点与符号位，避免交叉变异结果出现一串基因两位符号位或小数点.次数d和权值系数μ采用格雷码编码.指定参数寻优区间

C∈[2-8,28],ρ∈[2-8,28],d∈[1,3],μ∈

[0.1,0.9].当前迭代次数t←1，最大迭代次数

T=200.

(2)依据各条染色体基因编码中的参数在训练集上训练SVR模型，采用式(17)的均方误差作为适应度函数进行评估并排序，淘汰后10%个体，依据适应度大小按梯度选择复制，保持个体总数不变.

(17)

式(17)中:S为评估样本数目，fi为模型预测值，yi为真实值，γ为适应度.

(3)从种群随机选择2个染色体作为亲代染色体，每个染色体的选择概率依据式(18)计算.

(18)

式(18)中:p1(i)表示被选为亲代染色体的概率，γi为适应度值.

(4)将亲代染色体进行基因交叉重组，交叉算子如下：

(19)

(20)

(21)

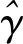
(22)

式(22)中:γi为突变个体适应度值，β2为调节因子.

t←t+1，若t≤T,则执行步骤2；否则执行步骤6.

(6)将当前种群中最佳适应度染色体的基因编码作为最优解解码输出，即得C、ρ、d、μ的最优参数值，依此在训练集训练最终的SVR预测模型.

遗传算法具备自适应和自学习性，其从问题解域搜索的并行化实现使得在参数寻优中避免了陷入局部最优的风险.

3 实验与结果分析

为了验证本文模型的有效性，本节介绍实验设置以及与其他模型的对比分析.

3.1 数据集及实验参数

本文使用Google云公开数据集，数据来自Google云计算中心Borg集群计算单元的工作负载.CusterData2019数据集提供了2019年5月8个cells跨度30天的资源请求、调度与任务记录，单个cell包含12 500台机器，672 000个作业，去除了终端用户对存储系统的访问模式等额外数据.数据集中的CPU使用信息依据5 m一个周期的频率采样汇总，同时包含带时间戳的内存、带宽等多维特征信息.本文筛选计算节点的数据子集作为需求序列信息，以前25天作为训练集，后5天作为测试集.

对输入数据进行预处理.利用线性插值法填补空缺值，为了使模型性能不受大规模输入样本影响，再通过中心化和归一化得到均值为0的规范化输入.模型的训练和测试采用深度学习框架Pytorch.卷积网络参数设置如表1所示.

表1 实验参数

实验中对切比雪夫多项式系数K∈{1,2,3}分别取值测试，预测误差随K值增大而减小，邻居节点超过3阶后卷积聚合不满足局部性要求.图卷积与时间维卷积均采用32个滤波器进行局部特征提取，以3个时间维周期采样片段作为3个通道(channel)，通过调整步长改变序列长度.学习率在对数尺度进行取样.优化算法采用小批量梯度下降(mini-batch gradient descent),实验中批处理大小(batch_size)取值过小其损失值随迭代会震荡式下降，故取样测试后在2的幂次方尺度以64为最佳.遗传算法获取的SVR最佳超参数分别为C=105.32,ρ=0.89,d=2,μ=0.6.寻优过程中的适应度函数变化曲线如图3所示.

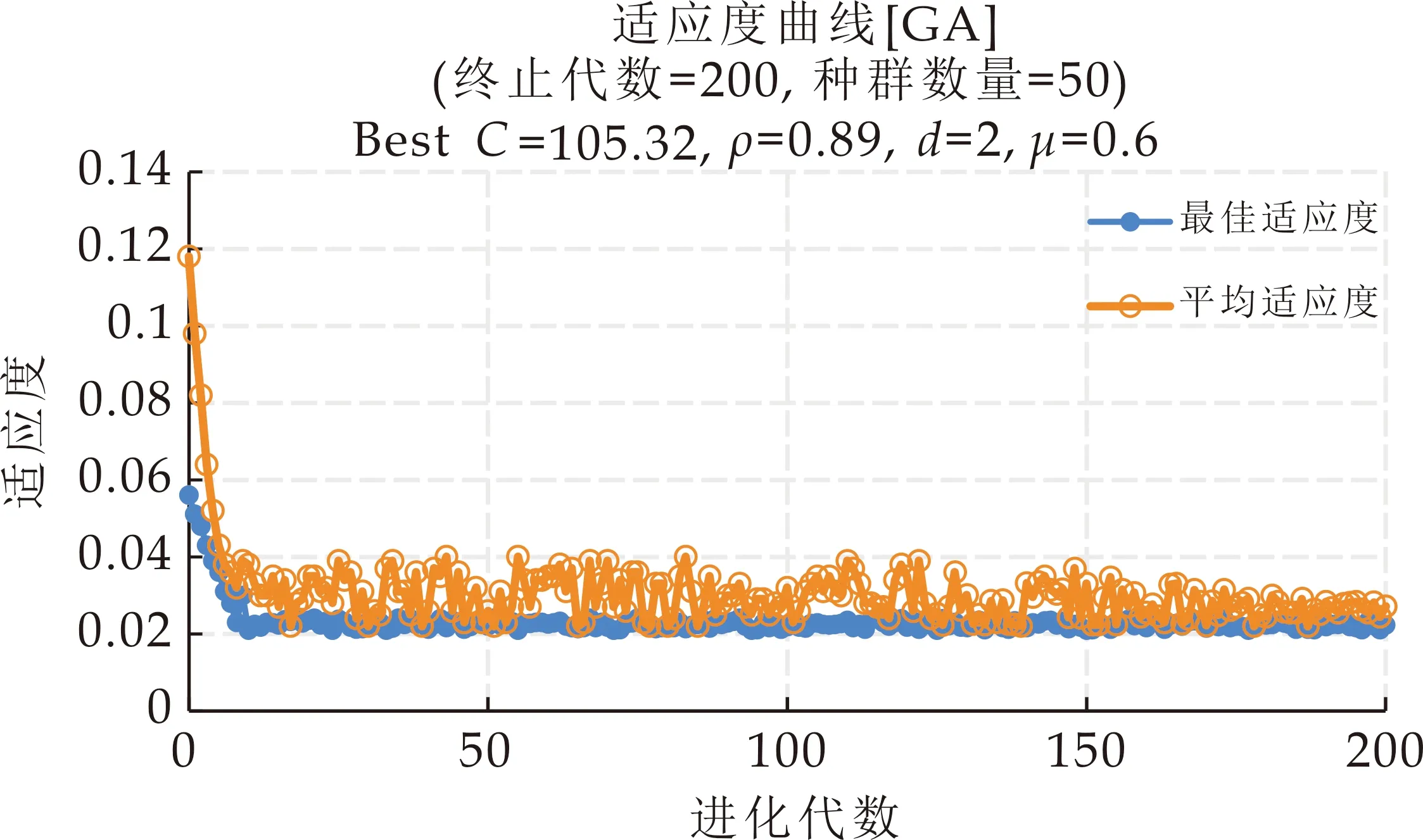
图3 遗传算法优化参数适应度曲线变化图

图中平均适应度在种群进化后期收敛到值域为[0.02,0.03]的小幅波动区间，最佳适应度在20代之后趋于稳定.

3.2 实验结果及分析

本文针对云资源预测模型的改进主要立足于支持向量回归与卷积网络的结合，具体创新点为融合图卷积的空间维建模以及对SVR的GA寻参优化.因此，本文基于支持向量回归和卷积神经网络分别选择对比模型，包括：本文提出的新的预测模型；本文未融合图卷积网络结构的(CNN-SVM)；文献[8]未进行GA寻优的支持向量机(SVM)模型；以及进行泛化对比的经典时序预测算法ARIMA、LSTM.

因为容器云平台的计算资源管理主要针对CPU与Memory进行，超过使用阈值即进行扩缩容响应，所以对比试验针对CPU利用率与Memory使用量序列进行预测研究.使用均方根误差(RMSE)、平均绝对误差(MAE)、平均绝对值百分比误差(MAPE)、平均均方误差(MSE)评估对比模型，计算式如下：

(23)

(24)

(25)

(26)

式(23)～(26)中:n为预测样本数，yi为实际值，fi为预测值.

各模型在测试数据集上对未来2 h每隔5 min的单步预测结果对比见图4和图5所示，以original表示原始数据，ours为本文模型.

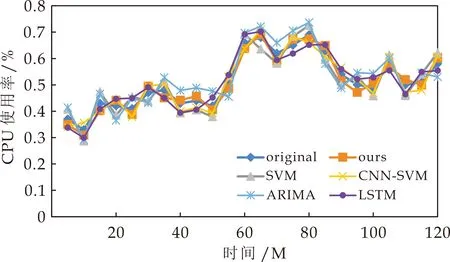
图4 各模型CPU预测结果对比

图5 各模型内存预测结果对比

从图4和图5的实验结果可以观察到，所有算法与原始序列的趋势基本一致，本文模型相比其他算法，取得了更加理想的拟合效果.同时也可以看到，CPU序列数据起伏波动较大，各算法相比内存序列在转折点处预测偏差更为明显.为了进一步量化对比结果，各模型具体误差统计见图6和图7所示.

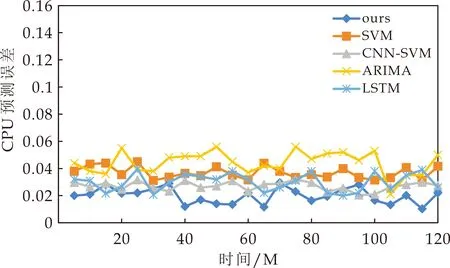
图6 CPU预测误差对比

图7 内存预测误差对比

从图6和图7可以更清楚地看到，在CPU和内存序列的预测中，本文模型相比其他方法具有更低的预测误差，且融合图卷积与GA优化的效果反映在图中表现为对CNN-SVM和SVM的明显精度优势，这说明本文的改进思路是有效的.但是也应当注意到，面对随机性更强且波动剧烈的CPU序列，各模型的预测稳定性显著降低，本文模型也出现了较为明显的精度波动，且相较于内存序列优势减小，这说明面对弱平稳的不规则波动，本文模型依然存在可优化空间，这也是未来的工作方向.各模型的详细误差指标如表2和表3所示.

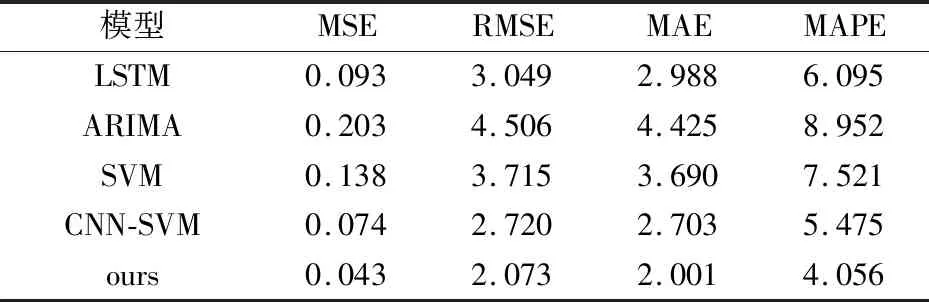
表2 预测性能对比(CPU)/10-2

表3 预测性能对比(内存)

云资源预测主要针对未来一段时间的变化趋势进行分析，单步预测结果只能描述下一时刻的资源变化情况，为了检验本文方法的泛化能力，每隔6、12、18个原始采集点分别求取平均，以此构建30 min、60 min、90 min间隔的资源序列作为新的训练样本，在测试集的多步预测结果如表4和表5所示.

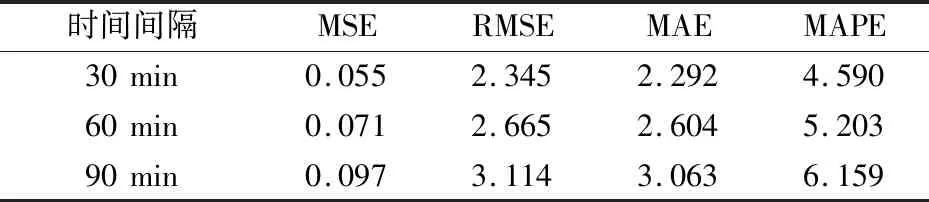
表4 不同间隔步长的预测性能(CPU)/10-2

表5 不同间隔步长的预测性能(内存)

从表中可以看到，随时间间隔增加，预测难度越来越大，但本文模型在不同步长依然保持较低的预测误差，能够稳定地描述资源的多步变化趋势，证明了模型的可靠性与稳健性，且具备一定的泛化能力.这为实际云场景中通过多步需求预测为基础平台的弹性承载力赋能提供了重要指导意义.

4 结论

本文提出一种基于卷积网络与支持向量回归的云资源预测模型，该模型结合图卷积与标准卷积提取网络拓扑下的时序数据特征，并利用遗传算法优化SVR预测性能.在谷歌云计算中心数据集上的实验表明，本文模型相比传统时序预测方法提高了预测精度与稳定性，提升了容器云平台的资源分配与调度效率.