Sklearn 数据挖掘技术在职业院校人才招聘中的应用
林海,叶小玲
(1.惠州城市职业学院,惠州 516001;2.惠州工程职业学院,惠州 516001)
0 引言
职业院校新兴专业岗位已经出现招聘多年,一无所获的情况。职业院校虽然有较多灵活的引入人才的机制,但缺乏预测应聘者入职学校意愿的研究。在现实招聘工作中,很多大学毕业生即使参加了笔试、面试、甚至体检,但最后放弃到学校任职的情况很多。对应聘者的入职学校的意愿进行分析,能够帮助人事部门与应聘者深化沟通,旨在提高招聘成功率。数据挖掘技术发展迅猛。近3 年,知网核心期刊收录的期刊文献有1908 篇,2020 年预测达1000 篇。如图1 所示。

图1 知网“数据挖掘”为主题的期刊发表年度趋势
数据挖掘技术被很多行业采纳,受到了学者们的关注,例如邵为爽等人(2020)数据挖掘在房地产价格预测中的应用研究[1];丁国勇(2020)在高校学生学业表现中展开了数据挖掘技术的研究[2];李铁波(2019)对学生行为特征分析与预测中运用了数据挖掘技术[3]。
在机器学习和统计领域,线性回归模型是最简单的模型之一。用回归方法进行预测的期刊文献2015-2020 年被知网收录的就有3932 篇。主要主题涉及回归分析、支持向量机、多元分析、预测精度、线性回归模型、logistic、主成分分析、随机森林等。如图2 所示。

图2 知网收录2015至今以“回归预测”为主题的期刊论文分布
线性回归、支持向量机、逻辑回归等被广泛采用。如陈战勇(2020)建立融入证据权重的逻辑回归用于预测客户违约情况[4];侯恩科等人(2020)的将回归分析方法用于矿井涌水水源识别[5];彭辉等人(2018)将回归模型用于铁路客运量预测[6];刘小英等(2020)大学生心理韧性对主观幸福感的预测研究[7];苏理云等人(2020)研究了逻辑回归模型的损失函数等[8];冷建飞等人(2015)多元线性回归统计预测模型的应用[9];毛瑛等人(2015)将其余模型与回归模型组合实施了卫生系统人力资源的预测[10];向红艳等(2020)基于 RF-LR 的高速公路逃费车辆状态预测模型[11];左妹华等人(2019)基于逻辑回归模型的消费者购买意向研究[12]。
但数据挖掘技术,特别是回归等算法在职业院校招聘人才的研究与实践较少。Python 在数据挖掘中,通过sklearn 方法,可运行线性回归算法、决策树算法、随机森林算法、逻辑回归算法等。因此,本次研究,将探讨数据挖掘技术在职业院校人才招聘中的应用,运用sklearn 数据挖掘技术,探讨特征提取、模型训练、降维与聚类的在数据挖掘中的应用;并比较逻辑回归、支持向量机、决策树、随机森林、K 临近分类器的准确率、召回率、F1Score 等指标,寻找回归、分类、聚类等算法在职业院校人才招聘业务中的应用价值[12]。
1 研究方法
1.1 Logiissttiicc回归模型
逻辑回归可用于分类。且主要用于两分类问题。函数logistic 被称为函数Sigmoid。它的函数形式为:
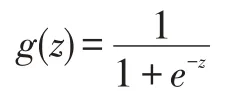
逻辑回归首先对决策边界建立回归方程,然后将回归方程映射到分类函数上以实现分类。例如,线性回归旨在能够依据历史记录,拟合给出1 条直线,利用这条直线对新的数据实时预测。其中,线性边界形式如下:

广义线性回归模型包含了逻辑回归。它的构造预测函数为:

函数hθ(x)可以用于表示类别0、类别1 的概率,它们公式分别如下:
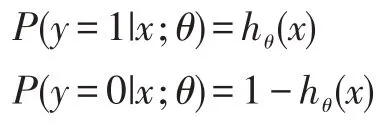
cost 函数的推导依据是最大似然,它的公式如下:

其损失函数计算方法如下:
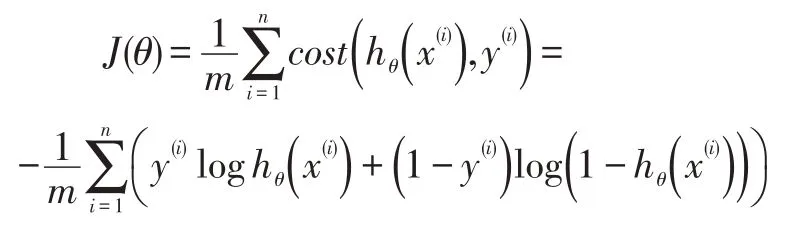
更新θ值中,应用了梯度下降算法,它的计算方法如下:
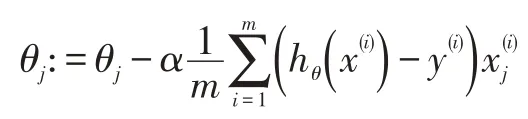
1.2 正则化Regularizaattiioonn
正则化能够降低模型的复杂程度,旨在提高模型应对新数据是有良好的预测。但有时候正则化会增加误差。在现实情况下,相对复杂的模型去训练模型时,往往得到比较好拟合效果,非常容易产生过拟现象,但去面对新数据时,效果却下降,缺乏泛化能力。正如在学习中,某些学生在平时模拟题目表现良好,但面对从来没有面对过的高考题,却表现糟糕,这就是过拟合[13]。线性回归算法、逻辑回归算法模型中,某权重设置的大小,会引发过拟合[14]。
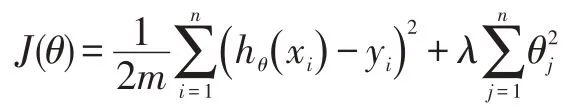
将之前损失函数,加上正则化项,对目标函数指定一些规矩。当λ值提高,这个限制机制更强[15]。通过L1实现正则,通过L2 防止过拟。为此,选择λ值要相当仔细,一般会让λ值慢慢变好,以观察数据的变化。
正则化后,更新θ值中,应用了梯度下降算法,它的计算方法如下:

L1 正则化可以容易获取稀疏的特征,相对而言,L2 正则化的应用比L1 广泛些。Python 中,只需要少量Scikit-Learn 代码,就可以运行正则化。
2 实证案例与分析
Python 3.7 环境中,numpy、pandas、matplotlib、seaborn 等包。数据集包括几个在主程序应用中重要的参数:Total Score(专业核心课程总成绩)、CET Score(英语成绩)、School Rating(学校级别)、BEH(从教意愿)、RM(求职资料评分)、INM(试讲评分)、ORTeach(是否有教学经历)。
目标值:Admit(入职学校意向)。
2.1 统计描述与特征初探
Total Score(专业核心课程总成绩)均值为346.653846、CET Score(英语成绩)均值为 492.374359、School Rating(学校级别)均值为 3.074359、BEH(从教意愿)均值为3.416667、RM(求职资料评分)均值为3.411538、INM(试讲评分)均值为 8.604487;ORTeach(是否有教学经历)为分类变量,1 表示“是”,0 表示“否”。样本量为390 个。Total Score(取值范围320-370)、CET Score(取值范围 477-505)、School Rating(取值范围 1-5 个级别)、BEH(取值范围 1-5)、RM(取值范围 1-5)、INM(7.2-9.92)、ORTeach(0 或 1)。Total Score(标准差 11.5)、CET Score(标准差 6.09)、School Rating(标准差 1.13)、BEH(标准差 1.003)、RM(标准差0.91)、INM(标准差 0.599);Total Score(较高值 355)、CET Score(较高值 497)、School Rating(较高值 4.0)、BEH(较高值 4.0)、RM(较高值 4.0)、INM(较高值9.06)。如图 3 所示。

图3
对比 Total Score、CET Score、School Rating、BEH、RM、INM、ORTeach 各变量与 Admit 的关系,以及变量之间的关系,并用散点图来显示。发现专业核心课程总成绩与试讲评分有明显的正相关关系。如图4 所示;将是否具有教学经历ORTeach 对图4 的特征进行分类,没有呈现明显的关系。如图5 所示。
将试讲评分与专业核心课程总成绩进行比较,并以散点图形式呈现,用sns.regplot 绘制回归线,试讲评分与专业核心课程总成绩有较强的正向关系,如图6所示;从教意愿与试讲评分存在较强的正向关系,如图7 所示。但此时回归线不具备明显的意义。

图4

图5

图6

图7
用sns.heatmap 绘制热力图,展示专业核心课程总成绩、英语成绩、学校级别、从教意愿、求职资料评分、试讲评分、是否有教学经历、入职学校意向多个变量的相关关系矩阵。初步判断:最有可能影响入职学校意向是专业核心课程总成绩(与Amit 相关系数为0.75)、英语成绩(与Amit 相关系数为0.73)、试讲评分(与Amit 相关系数为0.72);可能影响较小为是否具备教学经历(与Amit 相关系数为0.49)。如图8 所示。
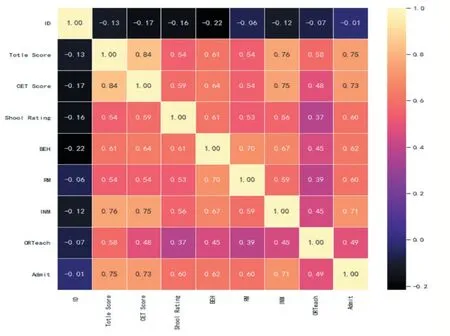
图8
用hist(柱状图)初探,候选人的专业核心课程综合评分的频率,密度较为集中为340-360 之间,在这个范围以上是候选人脱颖而出的一个很好的特征。如图9所示。
从图10,学校级别(办学质量)越高,候选人的试讲评分往往随之提高,如图11 所示;专业核心课程总评明显与试讲评分存在正向的关系,如图12 所示;从教意愿较强的,试讲评分有提升的趋势,如图11 所示。

图9

图10

图11

图12
2.2 训练模型
去掉ID 字段,用train_test_split 将数据集划分为训练集(占比为80%)、测试集(占比为20%);并运用MinMaxScaler 对数据取值范围缩放到固定范围(取值从0-1)。分别用线性模型、随机森林、决策树实施训练。线性模型R2 为0.669349356777144、随机森林 R2 为 0.6785217580151383、决 策 树 R2 为0.5074934372008834。从线性模型、随机森林、决策树三种模型的预测值与真实值的拟合图,分别如图13、图14、图15 所示。从3 个图得知,线性模型随机森林性能优于决策树。但应聘者既然进入了面试、试讲等环节,是非常有可能入职学校的,没有得到很好的预测。

图13
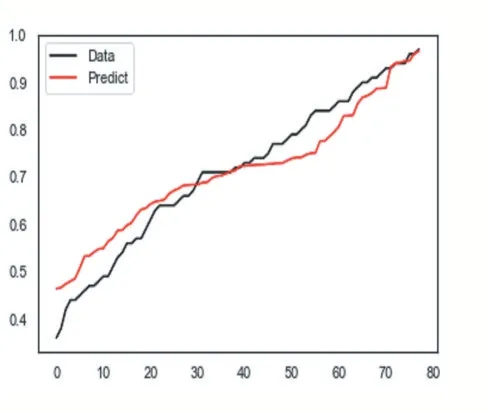
图14
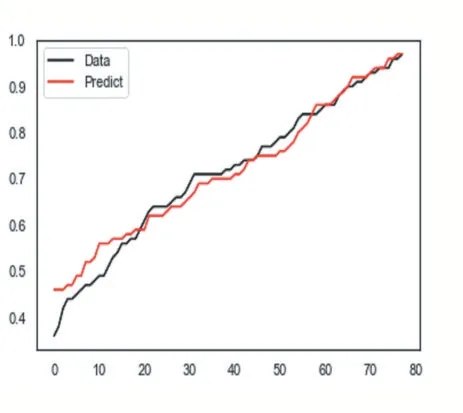
图15
2.3 特征分类与挖掘
若候选人的入职学校意向大于80%,则该候选人将获得1 个标签。如果候选人的入职学校意向小于或等于80%,则该候选人将获得0 标签。并利用混淆矩阵观察TP、FN、FP、TN 指标。调用多种模型进行比对,并且观察Precision(精确率),观察Recall(召回率),观察F1 Score 指标。
(1)实施逻辑回归:实施逻辑回归的精确率是0.9047619047619048,如图16 所示;实施逻辑回归的召回 率 是 0.76,如 图 17 所 示 。 其 中 ,F1Score 是0.8260869565217391。
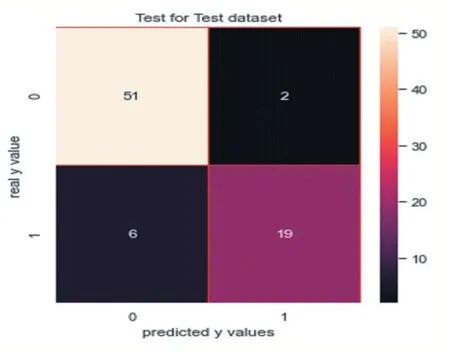
图16

图17
观察此混淆矩阵得知,在训练集样本上,有36 个分错的样本,有73 人想入职学校;在测试集上有6 个分错的样本。
(2)实施支持向量机:实施支持向量机的精确率是1.0,如图18 所示;实施支持向量机的召回率是0.68,如图 19 所示。其中,F1Score 是 0.8095238095238095。
观察此混淆矩阵得知,在训练集样本上,有27 个分错的样本,有79 人想入职学校;在测试集上有8 个分错的样本。
(3)实施朴素贝叶斯算法:实施支持朴素贝叶斯算法的精确率是0.8461538461538461,如图20 所示;召回 率 是 0.88,如 图 21 所 示 。 其 中 ,F1Score 是0.8627450980392156。

图18
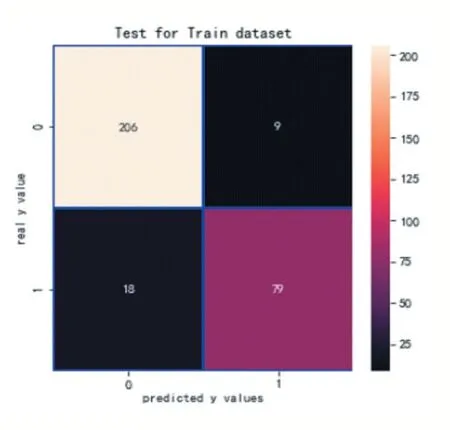
图19

图20

图21
观察此混淆矩阵得知,在训练集样本上,有50 个分错的样本,有81 人想入职学校;在测试集上有3 个分错的样本。
(4)实施决策树:实施决策树的精确率是0.88,如图 22 所示;召回率是 0.88,如图 23 所示。其中,F1Score 是 0.88。

图22
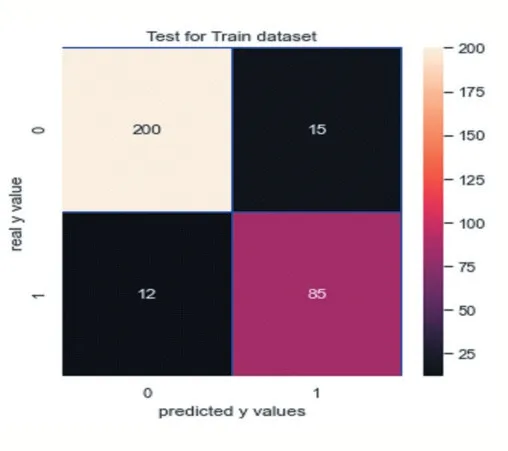
图23
观察此混淆矩阵得知,在训练集样本上,有27 个分错的样本,有85 人想入职学校;在测试集上有3 个分错的样本。
(5)实施随机森林:实施随机森林的精确率是0.9473684210526315,如图 24 所示;召回率是 0.72,如图 25 所示。其中,F1Score 是 0.8181818181818181。

图24
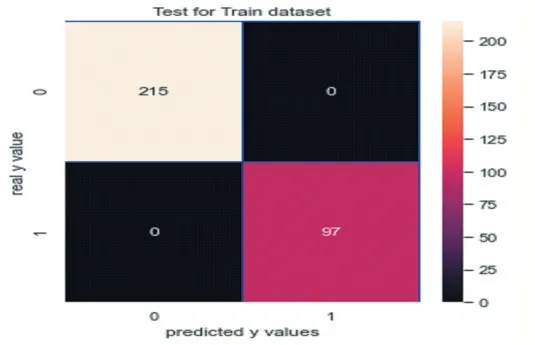
图25
观察此混淆矩阵得知,在训练集样本上,有0 个分错的样本,有97 人想入职学校;在测试集上有7 个分错的样本。
(6)实施K 临近分类器:实施K 临近分类器精确率是1.0,如图26 所示;召回率是0.68,如图27 所示。其中,F1Score 是 0.8095238095238095。
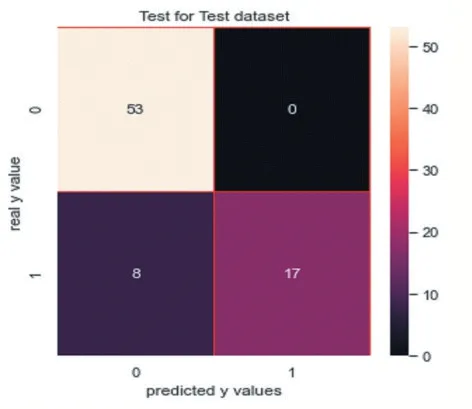
图26

图27
观察此混淆矩阵得知,在训练集样本上,有35 个分错的样本,有70 人想入职学校;在测试集上有8 个分错的样本。
比较逻辑回归、支持向量机、朴素贝叶斯、决策树、随机森林、K 临近分类器,可以得知,各类算法的效果预测效果良好。如图28 所示。

图28
2.4 降维与聚类分析
高维数据务必要重视,因此训练高维数据集时,往往引发维度灾难。通过降维将高维数据集降到三维、二维,人们才能更好地理解数据。数据在低位空间将更加容易出来,而且保留了相关特征,让重要特征得以在数据中明确显示。降维还可以减少噪声,并能够大大降低算法的开销[16]。PCA(主成分分析法)广泛被采用。这里,我们通过降维可以得到主要影响Admit(入职学校意愿)的主要特征:专业核心课程总成绩、英语成绩、试讲评分等。依据影响入职学校意愿排名较高的几个特征,能够实施K 均值聚类,层次聚类,以探求最佳的聚类参数取值。
(1)实施K 均值聚类:观察得知,最佳聚类数是3。数据集分成三个类别,一部分是决定到学校入职,一部分是选择放弃,还有一部分处于犹豫中的,但是入职学校可能性较大。
(2)实施层次聚类:采用树形图方法确定了层次聚类的最佳聚类数又是3。如图32、图33、图34 所示。
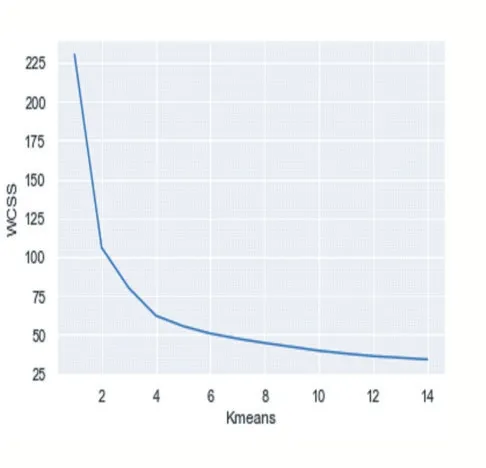
图29

图30

图31

图32

图33
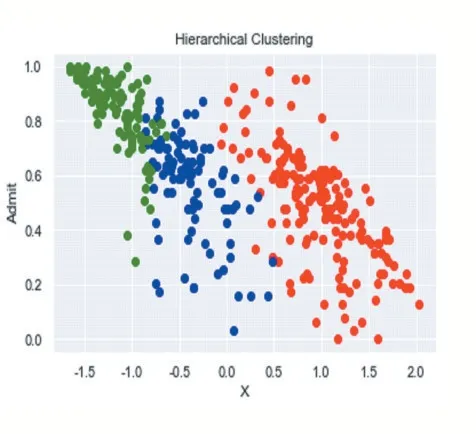
图34
可以得知,k-均值聚类和层次聚类是相似的。
(3)降维前后r2 比较:以逻辑回归算法为例,降维前 r2 是 0.669349356777144,降 维 后 r2 是0.6844177463055583。保持了较好的解释力度。降维会造成部分的信息损失,但能够节约时间与成本。
3 结语
此次,结合Sklearn 数据挖掘技术,将数据集中的Total Score(专业核心课程总成绩)、CET Score(英语成绩)、School Rating(学校级别)、BEH(从教意愿)、RM(求职资料评分)、INM(试讲评分)、ORTeach(是否有教学经历)等特征,包括目标值Admit(入职学校意向),实施了统计分析描述,对应聘者数据实施了探索,对比Total Score、CET Score、School Rating、BEH、RM、INM、ORTeach 各变量与Admit 的关系,以及变量之间的关系,并用散点图来显示,能够发现变量间明显的关系;通过热力图的相关系统中,得出了影响入职学校因素的专业核心课程总成绩、英语成绩、试讲评分的初步判断;并在实施归一化压缩后,实施并比对了线性模型、随机森林、决策树三种模型的预测值与真实值的拟合图,在训练模型中,线性模型、随机森林性能优于决策树;为进一步挖掘数据,将特征进行分类,并利用混淆矩阵观察 TP、FN、FP、TN 指标,实施了决策树算法、逻辑回归算法、朴素贝叶斯算法、K 临近分类器算法,通过比较得知各类算法的效果预测效果良好;聚类分析之前,运用PCA 实施了降维,对应聘者数据实施了K均值聚类、层次聚类,并得知此数据集最佳聚类数为3。最后比对了降维后的预测效果,模型保持了良好的解释力。综上职业院校人才招聘业务中,数据挖掘技术除了提供较为直观的统计描述,亦能够实施回归、分类、聚类等方法,数据都可以进行回归,分类,聚类的算法,得到了较好的预测效果。加上丰富的图表功能,Sklearn 数据挖掘技术将助力职业院校提升招聘效能,争夺到宝贵的人才资源。
由于此次样本量较小,算法的实验与测试受到了限制。不同算法的收敛时间缺乏比对意义。另外,逻辑回归算法采用默认参数,没有进行调参的比对。今后,不同岗位应聘者特征工程、各类算法模型的参数设置需要继续探讨,旨在优化算法,帮助招聘工作者招揽到合适大学毕业生到校任教任职,并期望为其余类别的招聘工作提供参考。

