借助函数对称的特性 实现问题简单化

吴大良

(江苏省射阳县陈洋中学 224361)

函数的有关性质是高中数学经常考查的内容，也是高考考查的重点对象.对称性作为函数的基本性质之一，广泛存在数学问题当中.利用函数的对称特性，可以使得某些问题简单化，使得问题更加简洁高效地解决，充分展现数学的美.下面通过例题，介绍函数对称性在解题中的具体应用.

一、二次函数对称性问题

二次函数是高中数学中极其普通常见的函数，是非常重要的函数，其存在广泛的应用空间.借助二次函数的对称性，可以提高解决关于对称方程根的问题的效率，尤其是在选择题中，借助对称的特性进行相互转化，方便找到解决问题的入口，如：

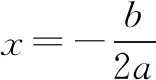
A.{1,2} B.{1,4}

C.{1,2,3,4} D.{1,4,16,64}

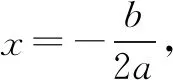
反思二次函数关于某条直线对称实际就是告知二次函数的对称轴是什么，要善于将问题中的信息进行等价转化.

二、三角函数对称性问题

除二次函数以外，三角函数也是数学中十分重要的函数之一.正弦函数、余弦函数不仅仅是周期函数，更是对称性的函数.因此，在利用正余弦函数的对称性时，有时还要考虑周期性，如：

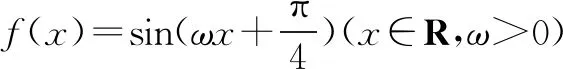
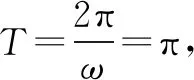
反思：正弦函数与余弦函数在利用对称性解决问题时，一定要考虑定义域和函数的周期性，避免出现错解.

三、奇偶函数对称性问题

奇偶函数是函数中的一种特殊的函数，一旦问题中提及到函数是奇函数或是偶函数，相当于告诉我们函数的定义域满足的条件和奇偶函数的性质.无论奇函数还是偶函数的定义域都是关于原点对称，不同的在于奇函数的图象是关于原点成中心对称，而偶函数的图象关于y轴成轴对称.因此，把握最经典也是最简单的奇偶函数的对称性质，可以实现快速解题，如：

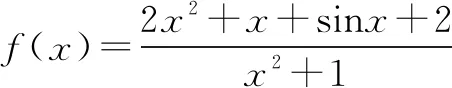
A.3 B.4 C.5 D.6

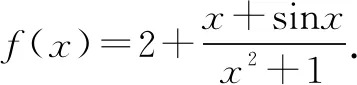
g(x)是奇函数，且函数关于原点对称，因此函数g(x)的最大值与最小值是互为相反数.所以f(x)max+f(x)min=[2+g(x)max]+[2+g(x)min]=4+g(x)max+g(x)min=4+0=4，故选择B.

反思此题借助函数奇偶性判断出函数具有的相关性质，奇函数的最大值与最小值的和是为0的，体现了数学上设而不求的思想，搭建到达问题彼岸的桥梁.此外，此题也对奇函数的图象的对称性和分离常数等知识进行综合的考查与研究.

简而言之，函数的对称性非常多，无法一一详述，也不可能将所有的对称性问题全部举例.因此，在日常学习中，可以关注常见的利用对称性解决问题的题型，通过不断积累，找到解决问题的快捷高效的方法.