大胆猜想 数形求证

王苏文

(浙江省诸暨市浬浦中学 311824)

普通高中数学课程标准(2017版)指出，数学学科核心素养包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析.在学习数学和应用数学的过程中，学生能发展数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析等数学学科核心素养.本文以2019年浙江高考第16题为例，阐述如何在数学素养下求解问题.

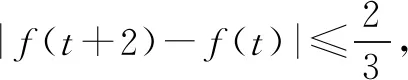
从试题来看，题干清楚、简洁，但有难点，尤其是存在性与任意性的问题对于学生而言始终是个难点.本题主要考查函数、不等式(含绝对值)等高中数学的基础知识，多角度、多层次地考查函数方程思想、数形结合思想等数学思想，同时也深度考查数学抽象与逻辑推理等数学学科核心素养，属于中等题.试题背景熟悉，学生容易入手，试题设计上能适合不同能力层次的学生.

本题在很多杂志上都有相应的佳作，在阅读杂志过程中头脑中有这样一个想法，注意到函数发现f(x)为奇函数，图象关于原点对称，同时f(x+2)-f(x)的横坐标之差为定值，结合浙江高考题的命题理念(高考命题数学组的试题评析和命题思路报告中提到：从整体出发运用合理的算法快速求解问题，这种“想得多一点，算得少一点；想得少一点，算得多一点”的命题理念).

一、大胆猜想

高中数学课程标准指出：直观想象是指借助几何直观和空间想象感知事物的形态与变化，利用空间形式特别是图形，理解和解决数学问题的素养.主要包括：借助空间形式认识事物的位置关系、形态变化与运动规律；利用图形描述、分析数学问题.

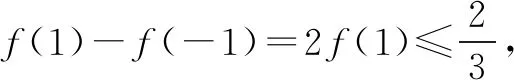
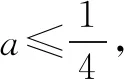
二、形的验证

为了证实这个问题的正确性，随后运用几何画板，通过图象来验证结果的可靠性，以下是几何画板的验证情况.

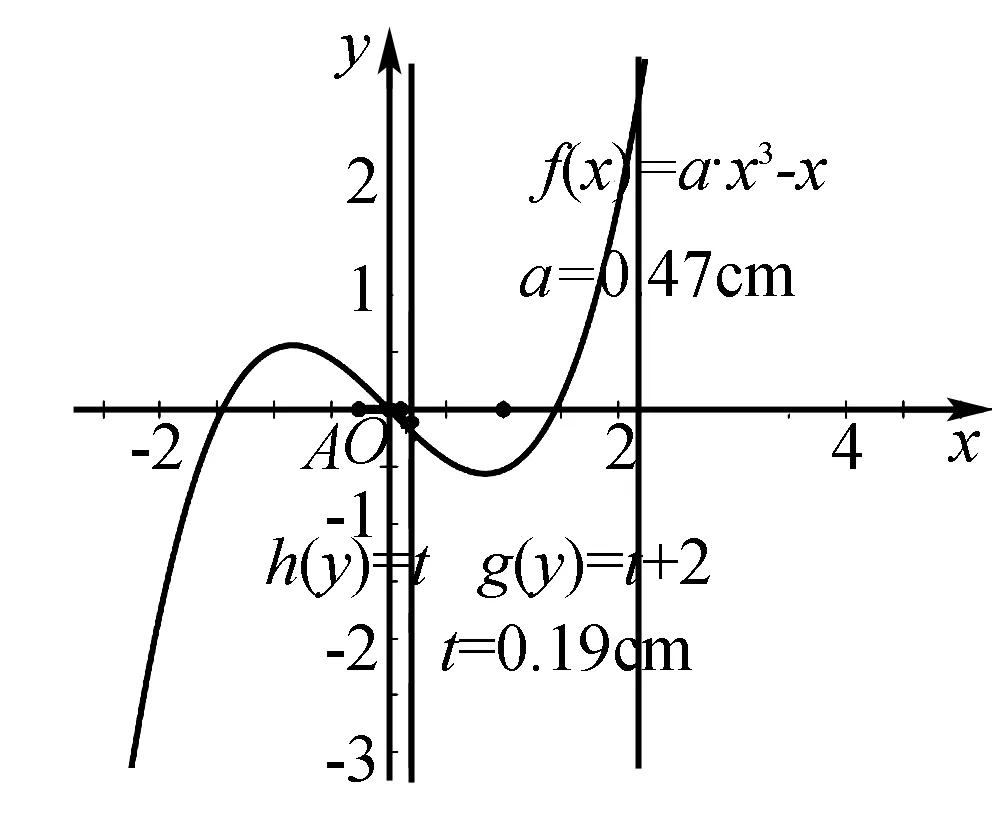
在实数a的变化过程中，夹在x=t,x=t+2的纵坐标之差最小值为恰好为t=-1时取到.

三、数的求证

高中数学课程标准也指出：数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题的素养.通过高中数学课程的学习，学生能进一步发展数学运算能力；有效借助运算方法解决实际问题；通过运算促进数学思维发展，形成规范化思考问题的品质，养成一丝不苟、严谨求实的科学精神.为了确保解题的严密性，笔者也运用最基本的运算方法进行解答.

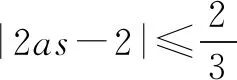
此法围绕函数思想进行求解，作为绝对值问题的常见方法为分类讨论，解法如下.

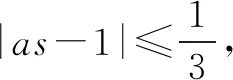
此法主要利用|x|≤m(m>0)⟺-m≤x≤m分类讨论去掉绝对值，同时运用分离变量法求函数的最值问题，使问题越来越简洁，明了.

四、几种视角

从数学的视角发现问题、提出问题，分析问题、建立模型，确定参数、计算求解，检验结果、改进模型，最终解决实际问题.本题可从以下几个视角进一步的思考：

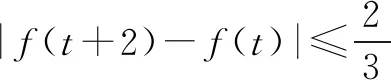
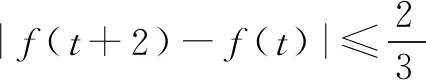
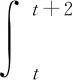
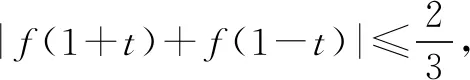
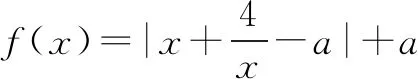
在平时求解过程中一方面要敢于大胆的猜想，而猜想的根源来于自己所掌握的知识和方法中所提炼的，同时也要能够进行严密的计算与验证，只有通过这样才能将数学学科素养得以在数学学习中不断提升.