利用隔项思想突破数列通项公式难题

高振宁

(山东省新泰市第一中学 271200)

数列问题是高考解答题必考题型，随着高考命题改革的进行，此类考查形式变化较大、有一定的解答技巧.此类问题的本质是数列的通项公式与数列求和问题，而解决的关键是求解数列的通项公式.为此笔者就利用隔项思想求解数列通项公式的方法介绍一下自己的浅见，试图建立解决此类问题的通法，供大家参考.

例1已知数列{an}满足a1=1，anan+1=3n，求数列{an}的通项公式.

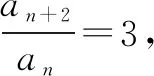
若不利用隔项思想：log3an+1+log3an=n，则令bn=log3an，则得

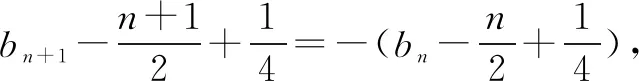
例2已知数列{an}满足a1=1，an+an+1=3n，求数列{an}的通项公式.

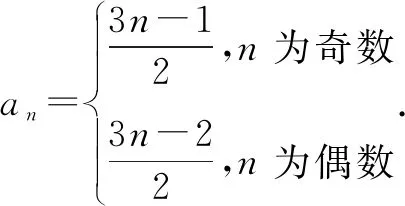
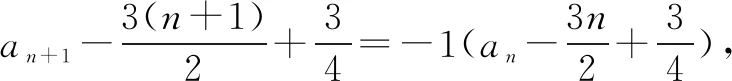
通过上述的两个例题，可以发现此类问题大都是以邻项和或邻项积的形式出现，解决问题的方法可以采取两种方式，第一种采取隔项思想解决，它的本质是在子列中构造等差数列或等比数列，上述例1的子列项的比值为常数，是等比数列，例2的子列项的差值为常数，是等差数列，且两个通项公式相对简单，便于应用解决数列的相关问题；第二种方法，直接构造等比数列，也可求出数列的通项公式，但是通项公式一般含(-1)n项，公式本身很复杂，很抽象，应用价值不大，即使要应用也需要利用分类讨论去掉(-1)n项，最终得到利用隔项思想得到的通项公式,这体现了隔项思想的巨大应用应用价值.隔项思想处理此类问题的本质是寻找子列当中的等差或等比数列，而直接求解是整个数列构造公比为-1的等比数列，它们都是构造数列，只是处理的的角度不同.

利用隔项思想处理问题的规律总结：

(1)题目中出现连续两项或几项的和与积，

(2)若是若干项的和，则连续两项作差；若是两项的差，则连续两项求和，若是若干项之积，则连续两项求商.

(3)解决问题的灵魂是构造等差数列或等比数列.

(4)求出的通项公式一般是分段形式，且与奇偶数有关.

(5)求出通项公式后，若求和一般也需对序号进行隔项求解，可以利用抽象问题具体化的思想来防止出错.

从下面两个例题来感受如何高效利用隔项思想.

例3(2012全国卷)数列{an}满足an+1+(-1)nan=2n-1，则数列{an}的前60项和为( ).

A．3690 B.3660 C.1845 D.1830

解当n为奇数时，an+1-an=2n-1，代入n+1得an+2+an+1=2n+1，两式相减得an+2+an=2，可知n为奇数时{an+2+an}为常数列，n为偶数时，an+1+an=2n-1，代入n+1得an+2-an+1=2n+1.

两式相加得an+2+an=4n，可知n为偶数时{an+2+an}为等差数列，则S60=(a1+a3)+(a2+a4)+(a5+a7)+(a6+a8)+…+(a57+a59)+(a58+a60)

=(a1+a3)+(a5+a7)+…+(a57+a59)+(a2+a4)+(a6+a8)+…+(a58+a60)

=2×15+(8+24+…+232)=1830，故答案是D.

实际上高考试题对连续两项的性质加入(-1)n后，使题目难度增大，但是根据上述规律2，n为奇数时求差，n为偶数时求和，最终得到了子列是等差数列，但是在求解出通项公式后，应用容易出错，n为偶数时，an+2+an=4n，若求S偶=(a2+a4)+(a6+a8)+(a10+a12)+…

则n的取值分别为2,6,10…，而不是2,4,6，…，这是解决此类问题的易错点，可以利用列举法来归纳规律.

例4设数列{an}的前n项和为Sn，an+1+an=2n+1，a2<2，则使Sn=2019的n的最大值为____.

解由题意an+1+an=2n+1，得an+2+an+1=2n+3，两式相减得an+2-an=2，故{a2n-1}是a1为首项2为公差的等差数列，{a2n}是a2为首项2为公差的等差数列,则

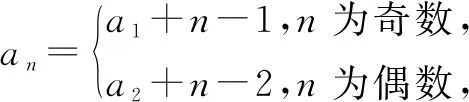
当n为偶数时,

Sn=(a1+a3+a5+…+an-1)+(a2+a4+a6+…+an)

=[a1+(a1+2)+(a1+4)+…+(a1+n-2)]+

[a2+(a2+2)+(a2+4)+…+(a2+n-2)]

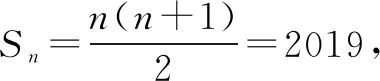
当n为奇数时,

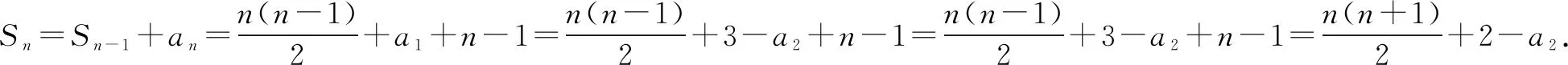
又因n∈N*，可知n≤63，故n的最大值是63.

此题是隔项思想求通项公式与基本不等式的知识的综合，在不知前两项的前提下，可以求出数列的通项公式与a1,a2有关，借助于分类讨论思想，利用分组求和方式求出数列的Sn，发现如下规律：

(1)当n为偶数时Sn与a1,a2都无关，仅与n有关，

(2)当n为奇数时Sn既可以写成与a1有关的解析式，也可以写成与a2有关的解析式.

(3)在利用求解不等式解决问题时注意变量的取值范围.

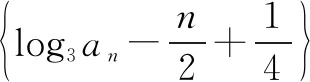
(1)若数列{an}满足anan+1…an+k=Mαn+β(k≥1,k∈N*,M≠0)成立，则数列{an}可以拆分成k+1个子数列，且每个子数列都为等比数列；

(2)若数列{an}满足an+an+1+…+an+k=αn+β(k≥1,k∈N*)成立，则数列{an}可以拆分成k+1个子数列，且每个子数列都为等差数列.

利用隔项思想解决邻项数列问题，值得我们进一步作深入的研究.