基于概率密度演化的风机基础疲劳可靠度计算

赵俭斌，王凯威，王一达，付兵†

（1.沈阳建筑大学 土木工程学院，辽宁 沈阳 110168；2.上海杰地建筑设计有限公司，上海 200085）

在过去20 年，风电持续高速发展[1-3]，到2018 年底，全球风电累计装机容量已突破600 GW，新增装机容量共53.9 GW.风机受到长期的动力荷载作用，疲劳问题突出，需要准确预测风机结构的疲劳损伤，尤其是在塔底动应力很高的地方.

影响结构疲劳损伤的因素甚多，其中荷载是最主要的方面，风荷载本质上具有不可忽略的随机性，因此，采用可靠度的分析方法分析结构疲劳损伤是一种自然的选择.

目前，可靠度的求解方法包括：Monte Carlo[4，5]、一次二阶矩[5]、响应面法[5]等.基于一次二阶矩理论的可靠度分析方法的主要目标在于寻求随机结构响应的二阶矩统计量.在获得二阶矩统计量之后，通过假定结构响应服从正态分布计算结构的使用可靠度.响应面法的基本思想是将功能函数的输入和输出变量表示为标准正态分布变量的多项式，而各变量的系数通过配点法（collocation points）确定，最后由功能方程得到可靠指标和失效概率.Monte Carlo 法虽然适用性较强，但以过高的计算量为代价.近年来陈建兵和李杰[7-9]发展了一类随机结构反应的概率密度演化方法，利用这种方法，可以精确定量地给出结构反应的演化概率密度曲线族，由此，可方便地根据指定的位移反应限值，直接计算给出随机结构在随机荷载作用下的可靠度.

对于风机这种新的结构形式，其受到的风荷载突出，随机风引起的疲劳损伤问题也更突出，但是有关风机结构的疲劳可靠度分析成果还很少.

本文基于概率密度演化思想，构造一个虚拟随机过程，使得随机结构时域内的疲劳损伤为该虚拟随机过程的截口随机变量.进而，建立概率密度演化方程并求解出随机结构疲劳损伤的概率密度，在安全域内积分给出结构的疲劳可靠度.

1 风荷载的数值模拟

设x，y，z 为空间中的一个点，其中z 是离地面的高度，x 是横向风向，y 是顺风向.在实践中，为了简化概念，风速波动可以在平面y=0 中表征[10].当只考虑竖向相关性时，风速场可以写成：

式中：符号θ 表示相应数量的随机性，V（θ；z，t）是高度z 处的风速（m/s），是高度z 处的平均风速（m/s），是风速的波动分量（m/s），假设为正常的零均值稳态随机过程.平均风速可用幂函数表示为[11-12]：

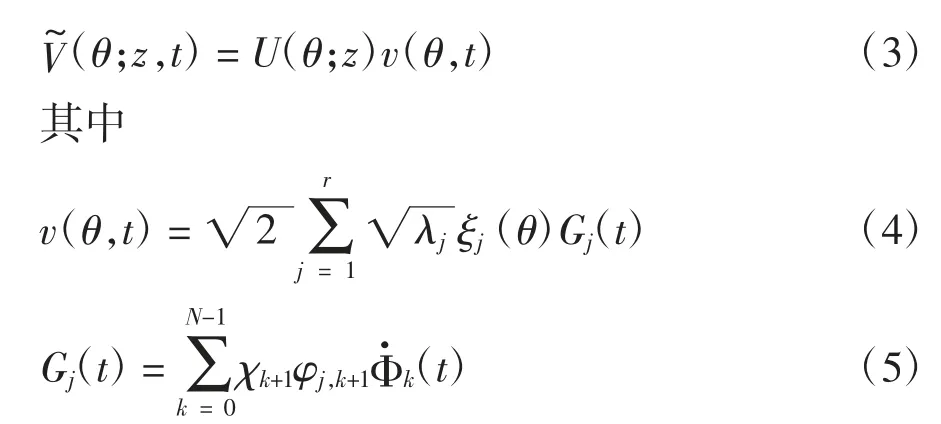
式中：·表示导数，χk+1为谐波能量调整系数，φj，k+1是标准特征向量Фj的k+1 个元素，λj和Фj分别是相关矩阵R 的特征值和特征向量[13]RФj=λjФj.R=[ρij]（N×N）.

无量纲的随机变量组{ξ1（θ），…，ξr（θ）}满足下列关系:

式中：δij为Kronecker-delta 符号.

式（3）中：

只考虑其中λzj和fzj（z）是特征值和相关函数RUz（z1，z2）的相应本征函数，可由Fredholm 积分方程得到

式中：δij为Kronecker-delta 符号.本文中rz=5.

2 疲劳可靠度分析的概率密度演化方法

在对风速进行正交展开后，可将展开结果代入塔身动力反应控制方程，求解控制方程进而可以得到对应不同θ 的动力反应（如塔身某点的速度），将对应于不同θ 的动力反应代入概率密度演化方程，将求解结果对θ 积分，可得所需要的动力反应随时间变化的概率密度.

风机结构的动力反应控制方程[14]为：

式中：M，C，K 分别为n × n 阶质量矩阵、阻尼矩阵与刚度矩阵，，X 为n 维加速度、速度与位移向量[13]，Q 为n 维激励即风荷载向量，θ 为反映激励随机性的随机矩阵，本文中此随机矩阵的行向量个数为15 个，行向量的维数遵循数论选点法[15，16].其概率密度函数pΘ（θ）已设定.

式中：μD为拉力系数，假定为1.2；ρ 为空气密度；Bj为塔身单元面积.Vj为风速（见式（13），与θ 有关）.

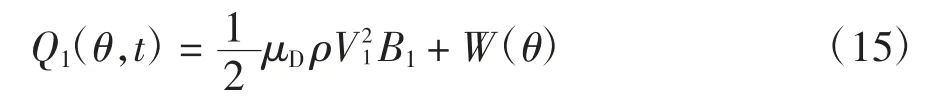
式中：W（θ）为用推力系数法[17，18]求得的由旋转叶片传递给塔身的风荷载推力，W（θ）=，r 为叶片长度，VT为塔顶风速，Thr为推力系数.

对于疲劳损伤D，就结构动力学问题而言，它必连续依赖于随机参数θ，构造以τ 为虚拟时间参数的虚拟随机过程Zl

显然，D（θ，T）为Zl在τ=1 时的截口随机变量，亦即：

（Zl，Θ）的联合概率密度函数的概率密度演化方程为：

其初始条件为：

求解偏微分方程初值问题（18）、（19）即可给出联合概率密度函数，进而给出Zl（τ）的概率密度函数

由式（17）可知，

由式（21）可方便地求解随机结构的可靠度，亦即：

3 疲劳累积损伤理论

损伤是指在循环荷载作用下材料的损坏程度，一般用一个无量纲参数D 来表示它，当D=0 时，说明材料完好无损，当D ＞1 时，表示材料已经达到它的疲劳寿命.

在随机荷载作用下，结构疲劳损伤分析采用疲劳累积损伤理论.目前普遍采用的理论有Palmgren[20]-Miner[21]线性疲劳损伤准则.

本文主要分析风荷载作用下风机塔身底部混凝土基础的疲劳可靠度，采用P-M 准则对应的S-N 曲线[22]为：

式中：Smax为风荷载作用下的应力范围，单位为MPa，Nf为对应Smax的导致材料发生疲劳破坏的循环次数.疲劳损伤D 的定义为

式中：nk为第k 级应力幅值下的实际循环次数，Nfk为第k 级应力幅值下达到疲劳破坏时的允许循环次数，由S-N 曲线查得.k 为计算疲劳损伤时所涉及到的所有工况所对应的应力幅值总数.

4 实例计算

本文基于某风电场3 MW 风力发电机进行建模分析.该风力发电机轮毂高度90 m，风轮直径100.8 m，额定风速11.9 m/s，设计寿命为20 年.基础混凝土采用圆形台柱式扩展基础，底板直径21.5 m，高3.9 m，埋深3.5 m.塔筒材料为Q345 钢材，基础环采用Q345 钢材，基础混凝土采用C35 混凝土，底部采用完全约束，采用ABAQUS 有限元软件建立模型，选用实体单元.表1 为各段塔筒的几何参数，采用的ABAQUS 中混凝土损伤本构模型如图1 所示.

表1 塔身风荷载计算参数Tab.1 Calculation parameter of wind load of tower body

图1 混凝土损伤本构模型Fig.1 Concrete damage constitutive model

图1 中，fcm为屈服强度，εc1为屈服应变，Ec为弹性模量，dc为损伤因子，为非线性应变，为塑形应变，为弹性应变，σc为压应力，εc为压应变，dc=取值为0.35～0.7，应力应变关系由混凝土规范[23]提供，将相关参数输入软件中计算可得所需数据.

4.1 风荷载的计算

平均风速的选取考虑到轮毂处的工作情况，根据平均风速的指数模型计算可选取相应10 m 处平均风速（标准平均风速）12 m/s.

在计算方程（18）时，令θ=θq，θq=（θ1，q，θ2，q，…，θs，q）（s=15，q=1，2，…，Nsel），将对应θq的D（θq，T）代入方程中，可得联合概率密度函数，进而对方程（20）积分并结合式（21）和（22），最终可得D值的疲劳可靠度.关于Nsel的选取遵循数论选点法，在Matlab 中实现选取步骤，对n=2 422 957 的随机列向量采用数论选点法[10，15，16]进行筛选，得到Nsel=182 个随机列向量组，依次编号1、2、3…，方便后续整理计算.

在这182 个随机列向量组的基础上，根据算法在Matlab 中进行编程，独立地生成标准平均风速为12 m/s 时的182 种风速时间历程，每一个随机列向量对应生成一个风速时程，将脉动风速时程继承随机列向量的编号，并将脉动风时程与平均风时程合并，可得到轮毂处的总风速时程，如图2.

图2 标准平均风速为12 m/s 轮毂处总风速Fig.2 Total wind speed at hub with standard average wind speed of 12 m/s

为了验证风速模拟数值的准确性，在平均风速为10.27 m/s 时进行实测，实测风速的采样频率为1/7 Hz，选择的实测风速为风向稳定且基本与应变测点一致的时间段，实测结果如图3.采用文中所述方法展开风速为10.27 m/s 时结果如图4.

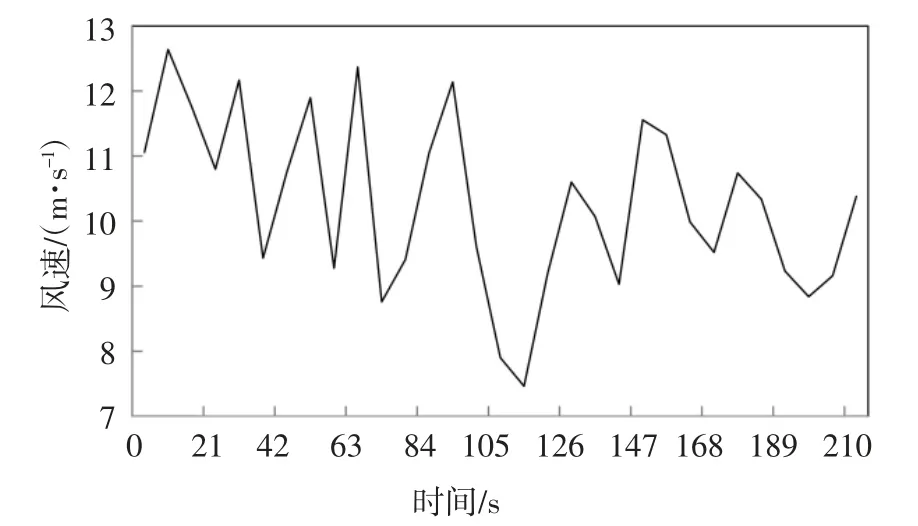
图3 平均风10.27 m/s 的实测风速Fig.3 Measured wind speed with an average wind of 10.27 m/s

由对比可知，文中风速展开方法与实测值趋势大体一致，可以由此确定风速模拟取值的正确性.

图4 平均风速为10.27 m/s 模拟风速Fig.4 Simulated wind speed with an average wind speed of 10.27 m/s

4.2 风机动力响应的有限元模拟

将风荷载时程加载至风机模型上，可以得到各个随机风荷载下的风机动力响应，本文主要观察钢环与混凝土接触范围内的动力响应，取10 m 处平均风速为12 m/s.利用公式（14）、（15）计算塔身处各点的风荷载时程.

将风荷载加至有限元模型，并考虑塔身风荷载的影响，采用应力等值线来表示模型内部的应力分布情况，可以清晰描述外动力响应在结构中的分布，从而快速确定模型中的最危险区域.疲劳损伤的计算是在等效应力时程的基础上计算，因此提取基础环和基础的等效应力云图.本文提取182 种随机风荷载时程的第一和第二个时程，编号为1、2，编号1、2 动力响应下基础环和基础等效应力云图如图5所示.

图5 基础钢环应力云图Fig.5 Stress of the basic steel ring

由图5 可看出，基础环在与混凝土基础上部接触部位出现应力集中现象，初步验证了本文工况破坏发生的位置，进一步提取出编号1 动力响应混凝土基础的整体应力云图与剖面应力云图如图6 所示.

图6 编号1 风荷载作用下基础应力云图Fig.6 Stress cloud diagram of the foundation under number 1 wind load

同样，查看其他编号动力响应的应力云图与编号1 的结果进行对比，可看到应力最大的位置相同，区别只是应力大小和时程的变化.如图7 为编号2动力响应的风机基础的动力响应结果.

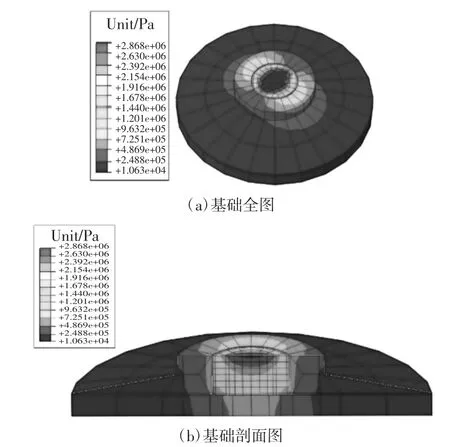
图7 编号2 风荷载作用下基础应力云图Fig.7 Stress cloud diagram of the foundation under number 2 wind load

由图6 和图7 可知，在顺风向的钢环内外侧与混凝土基础表面接触处，动力响应产生的混凝土应力值最大，此处为疲劳危险位置，符合实际工程发生的破坏位置.

经过对比发现钢环内侧混凝土的应力比外侧更高，这意味着，当工程实际遇到本文工况基础环外侧混凝土疲劳破坏时，其实钢环内侧混凝土接触部分更有可能已经破坏.提取危险点的应力响应，所有编号荷载作用下的危险点应力响应如图8 所示，编号1 对应的压应力时程如图9 所示，编号1 的雨流统计数据如图10 所示.由于风荷载是θ 的函数，故应力时程平均应力和最大幅值随θ=182 而变化，由图8可见，最大应力幅值可达10 MPa.

图8 危险点动力响应结果Fig.8 Dynamic response results at dangerous points

图9 编号1 风速对应的危险点应力时程Fig.9 Stress time history of dangerous points under number 1 wind load

图10 编号1 应力时程降雨计数矩阵Fig.10 Stress time history rainfall counting matrix of number 1

根据有限元模拟所得的应力时程运用雨流计数法进行求解疲劳损伤，根据雨流计数法的基本思想在Matlab 中进行编程，得到雨流计数结果之后可将结果进行等效应力修正，结合选取的S-N 曲线对所有编号响应情况的应力时程根据线性叠加理论进行疲劳损伤计算，结果如图11 所示.

图11 疲劳损伤Fig.11 Fatigue damage

图11 的疲劳损伤值为加载时长600 s 时的过程所造成的疲劳损伤，将求解出的疲劳损伤转化为以秒为单位，将之与所需计算的加载时长相乘即可得到所需年限的疲劳损伤，以此可以分别计算出使用时长10 年～30 年时危险点处的疲劳损伤累计值.

将疲劳损伤定义为关于τ 的随机过程，即虚拟随机过程，并进一步进行离散，采用单边差分法进行计算方程（18）的数值解.

采用单边差分方法时，其中时间步数为100，步长为0.01 s，疲劳离散步数为50 步，离散区间为[0，5]，每一编号对应的疲劳损伤结果都作为初始条件进行一次计算，将计算所得所有编号的疲劳概率分布离散数值解相加，可以得到此年限下的概率密度数值解，不同年限时，代入不同的疲劳累计损伤即可得到该年限下的疲劳破坏概率密度数值解，全部结果展示如图12 所示.其中疲劳破坏年限为30 年、20 年和10 年的概率密度离散值如图13 所示.

由图11、图12 可看出，使用时间越短时，疲劳损伤累计值小于1 的概率分布越多，随着年限增加疲劳概率密度曲线总体呈现向疲劳损伤大于1 的方向偏移的趋势.

图12 各年限下疲劳损伤概率密度数值解Fig.12 Numerical solution of probability density of fatigue damage under various years

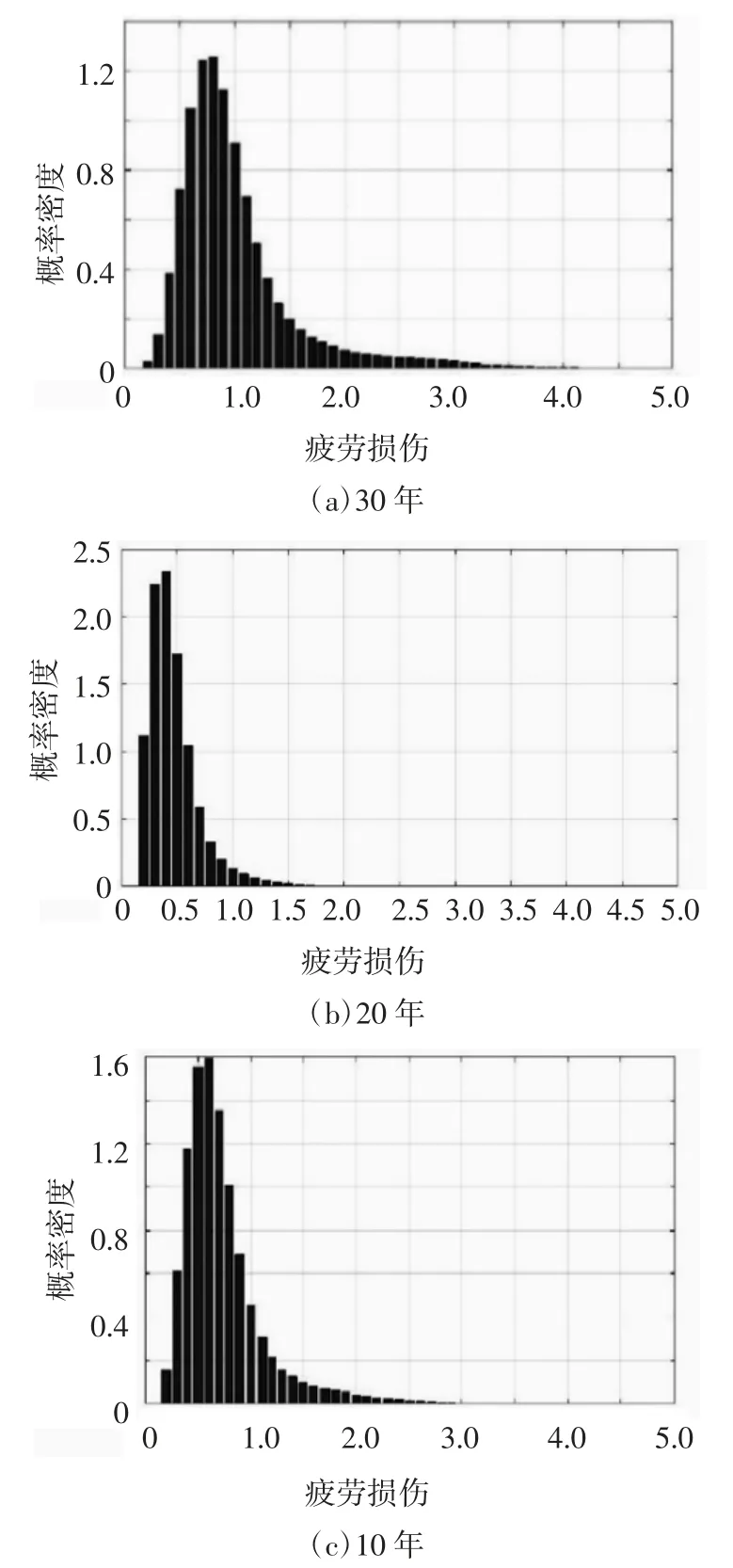
图13 疲劳概率分布离散数值解之和Fig.13 Sum of the discrete numerical solutions of the fatigue probability distribution

当疲劳损伤值在1 以下时，钢环侧混凝土不会发生疲劳破坏，换言之，结构处于安全状态.将疲劳损伤值为1 以下的疲劳概率进行数值积分，即为结构处于安全状态的概率，即为结构的安全可靠度.可靠度计算结果如图14 所示.

图14 疲劳可靠度Fig.14 Fatigue reliability

由图14 可见，随着时间的增加，疲劳可靠度不断降低，随着年限的增加，疲劳可靠度的降低呈现不断加快的趋势.当年限到达30 年时，疲劳可靠度为76.66%，风机使用时长20 年时，疲劳可靠度为94.67%.从已有文献[24]来看，风机在使用寿命20 年内，基础环附近混凝土发生疲劳破坏是真实存在的.

5 结论

本文主要研究了陆上风机在风荷载作用下混凝土基础的疲劳可靠度，具体结论如下：

1）根据随机动力作用的正交展开法和数论选点法，将风荷载展开为分散点集，由此进行动力荷载的计算较为合理.这种方法是用概率密度演化方法求解概率密度的前提和基础.

2）提出了一个基于概率密度演化方法的疲劳概率计算方法，将雨流计数法得到的疲劳损伤D 值代入概率密度演化方程进而求解基础处疲劳损伤的概率密度是一种有效的方法，不但过程简单，而且精度较高.采用概率密度演化方法，可精确定量地给出结构反应的演化概率密度曲线族，由此，可以方便地得出结构在随机荷载作用下的各种可靠度.给定阀值为1，通过对概率密度在小于阀值的范围内进行积分可得对应某风速的疲劳可靠度.

3）由表2 可以看出，本文所研究的混凝土基础的疲劳可靠度随着时间降低，当年限到达30 年时，疲劳可靠度只有大约76.66%，这意味着，风机基础有23.34%的概率发生疲劳破坏，这是一个非常危险的数值，结合本文实际工况实例中风力发电机的设计寿命为20 年，风机使用时间长20 年时的疲劳可靠度有94.67%，意味着疲劳破坏概率为5.33%，也印证了本文实际工况的发生并不是意外情况，尤其是在风机场的风机数量基数大的情况下，发生本文工况所示的疲劳破坏的概率还是不容小觑的.