反应谱兼容的时频非平稳地震动合成及其对结构非线性响应的影响

程顺，黄天立，李守文，2，王宁波

(1.中南大学土木工程学院，湖南长沙，410075；2.中建二局第一建筑工程有限公司，北京，100023)

地震引起的地面运动加速度不仅受时变振幅的影响，而且受时变频率的影响[1-2]。大量研究表明，地震动的时频非平稳性对结构反应尤其是非线性反应产生重要影响[3-5]。在进行复杂结构的时程分析中，常常要求采用与设计反应谱兼容的人工地震动作为输入，因此，研究能反映地震动时频非平稳特性且与反应谱兼容的地震动模拟方法具有重要意义。为了模拟时频非平稳特性且与反应谱兼容的人工地震波，CACCIOLA[6]将人工地震动合成分为2步：第一步由天然地震动记录生成具有时频非平稳特性的时程；第二步通过引入纠正随机过程使得生成的地震动与反应谱兼容。该方法引入了随机过程，增加了计算量。曲国岩等[7]通过引入具有统计参数的时频包线描述地震动非平稳特性，建立了与反应谱兼容的非平稳地震动模拟方法，该方法的关键在于如何获得具有统计意义的时频包线。张郁山等[8]通过增量加速度小波函数实现合成地震动与反应谱拟合，该方法具有较快的收敛速度，但小波函数的选取具有不确定性。OHSAKI[9]采用相位差谱替代[0，2π]均匀分布的随机相位以反映地震动频率非平稳的影响。国内一些学者[10-11]对相位差谱进行了深入研究，并模拟生成了人工地震波，但此类方法合成得到的地震动时频特性与天然地震动时频特性有较大差别。由此可见，上述反应谱兼容的地震动合成方法存在难以准确反映地震动时频特性或计算过程复杂等问题，存在应用局限性。自PRIESTLEY[12]提出演变过程理论以来，利用演化谱模拟地震动的研究得到很大发展。LIANG 等[13]由演化谱理论导出非平稳地震动过程模拟的一个谱表示方法，按照该方法可直接将样本过程由余弦级数公式计算。樊剑等[14]分别利用均匀调制非平稳模型和时变修正Kanai-Tajimi 非平稳模型模拟地震波的时变谱，建立了非平稳地震波的合成方法。何浩祥等[15]认为小波包分解方法是建立时变功率谱的有效工具，依据统一时频谱进行调整，人工合成的地震动具有较高的精度和较强的非平稳性。上述基于演化谱的合成方法未考虑如何使地震动与反应谱兼容。基于演化谱理论的方法模拟生成人工地震波虽然计算过程简单，但难以获取能准确反映地震动时频特性的时变谱。Hilbert-Huang 变换(HHT)方法[16]作为一种新的时频信号分析方法，其具有良好的时频局部化特性，可以更客观地估计地震的时变谱，从而模拟出时频非平稳特性且更符合实际情况的地震动时程。WEN等[17]用HHT变换得到天然地震动样本的Hilbert 谱，建立了非平稳随机过程合成方法，并且将该方法应用于多向量随机过程的模拟过程中。LI 等[18]基于Hilbert 谱建立了三向地震动的合成方法，通过HHT 变换调整合成的地震动的时频特性，可实现地震动时程的反应谱与目标反应谱兼容。楼梦麟等[19]指出，由HHT 方法中的经验模式分解(EMD)得到的固有模式分量(IMF)是不完全正交的，由此获得的Hilbert时频谱存在能量泄漏问题，进而会影响Hilbert 时变功率谱的估计。HUANG 等[20]进一步提出了3 种正交化经验模式分解方法即正交化HHT 方法，解决了Hilbert 时变功率谱估计中的能量泄漏问题，并给出了其在地震加速度谱分析中的应用。胡灿阳等[21]采用正交化HHT 方法，在估计Hilbert 时变功率谱的基础上，提出了基于正交Hilbert 谱模拟非平稳随机地震动的方法。陈清军等[22]结合演变谱理论和正交HHT 法的优点，提出了一种能同时反映强度和频率非平稳特性的地震动人工合成方法，但未考虑与反应谱的兼容问题。应该指出的是，基于演化谱和正交HHT 方法合成的人工地震动虽然可以准确地描述地震动的时频特性，且计算简单，但未考虑将合成的地震动与规范设计反应谱兼容的问题。为此，本文在陈清军等[22]提出的基于演化谱和正交HHT 方法合成地震动基础上，通过迭代调整时变功率谱，使合成的地震动时程反应谱拟合目标反应谱，提出一种与目标反应谱兼容的时频非平稳地震动合成方法；以El Centro 地震加速度时程南北分量作为种子地震动时程，设计与目标反应谱兼容的4 组加速度时程，分别对层数为7层和15 层的2 栋钢筋混凝土框架结构进行非线性时程分析，研究地震动时频非平稳特性对框架结构非线性响应的影响规律。

1 反应谱兼容的时频非平稳地震动合成方法

1.1 基于演化谱和正交HHT方法的地震动合成

首先选定种子地震动时程，通过HHT 或正交HHT 变换提取其Hilbert 时频谱，并根据Hilbert 时频谱估计其时变功率谱[21]，即

式中：f(t,wk)为时变功率谱；H(t,wk)为Hilbert时频谱。

将种子地震动时程的时变功率谱代入基于演化谱理论的非平稳地震动合成公式[22]，得

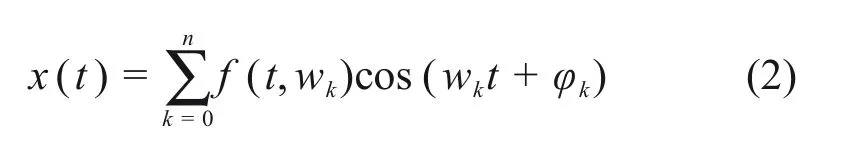
式中：x(t)为基于演化谱和正交HHT 方法合成的时频非平稳地震动时程；φk为[0,2π]上均匀分布、相互独立的随机相位角。

1.2 基于解析方法的反应谱计算

田玉基等[10]提出了先计算位移反应谱，进而求解加速度反应谱的方法，该方法可有效避免结构周期过短情况下积分步长的选择问题，使反应谱的计算更加便捷。该反应谱的计算流程简述如下。

单自由度结构在地震动a(t)作用下的运动方程为

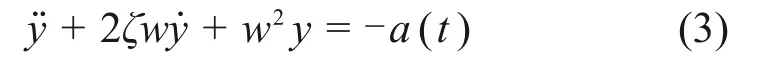
式中：w为结构自振频率；ζ为结构阻尼比；y，和分别为结构的相对位移、相对速度和相对加速度。

将式(3)改写成状态方程形式：

式(4)的解可写成如下迭代形式：

式中：A=eK•Δt；D=K-1(A-I)。

将式(5)展开，即可得到结构的位移响应时程及其峰值。对于不同频率控制点wi，可以得到其位移响应的峰值|yi,max|，即位移反应谱Sd(wi)=|yi,max|，进一步得到结构的加速度反应谱：

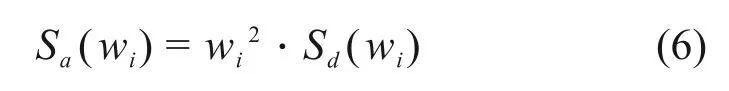
1.3 基于时变功率谱迭代调整拟合反应谱

通过迭代调整种子地震动时程的时变功率谱，直到合成的人工地震动时程反应谱以一定精度拟合目标反应谱为止。合成的人工地震动时程与给定的反应谱兼容，也准确地描述了种子地震动时程的时频特性。

定义调整系数Rj(wi)为n个频率控制点wi(i=1，2，…，n)处目标反应谱STa(wi)与经j次调整后地震动时程的计算反应谱Sja(wi)之比，即

对n个频率控制点wi处的时变功率谱f j(t,wi)乘以调整系数Rj(wi)进行迭代调整，得到调整后新的时变功率谱f j+1(t,wi)，即

式中：j表示第j次迭代。

为使合成的地震动时程反应谱以一定精度与目标反应谱拟合，采用式(9)定义的反应谱误差精度E(wk)，即

当E(wk)≤ε时，结束对频率控制点wk处的时变功率谱调整(其中，ε为设定的反应谱误差精度，本文取5%)。

时变功率谱经式(8)调整后，再采用1.1节基于演化谱和正交HHT方法合成人工地震动，重复1.2节和1.3节的步骤，直至合成人工地震动的反应谱以一定精度与目标反应谱吻合，由此得到与目标反应谱兼容且与种子地震动时程的时频特性一致的非平稳地震动。图1所示为此调整时变功率谱获得反应谱兼容的时频非平稳地震动合成方法流程图。

图1 反应谱兼容的时频非平稳地震动合成流程Fig.1 flowchart for simulating target response spectrum compatible time-frequency non-stationary ground motions

2 地震动时程方案设计及拟合结果

2.1 种子地震动及目标反应谱确定

选择1940-05-18 美国加州帝王谷(Imperial Valley)El Centro 台站记录的El Centro 地震加速度时程南北分量作为种子地震动时程，如图2(a)所示。图2(b)所示为基于正交HHT 方法获取的该地震动时程的正交Hilbert时频谱。

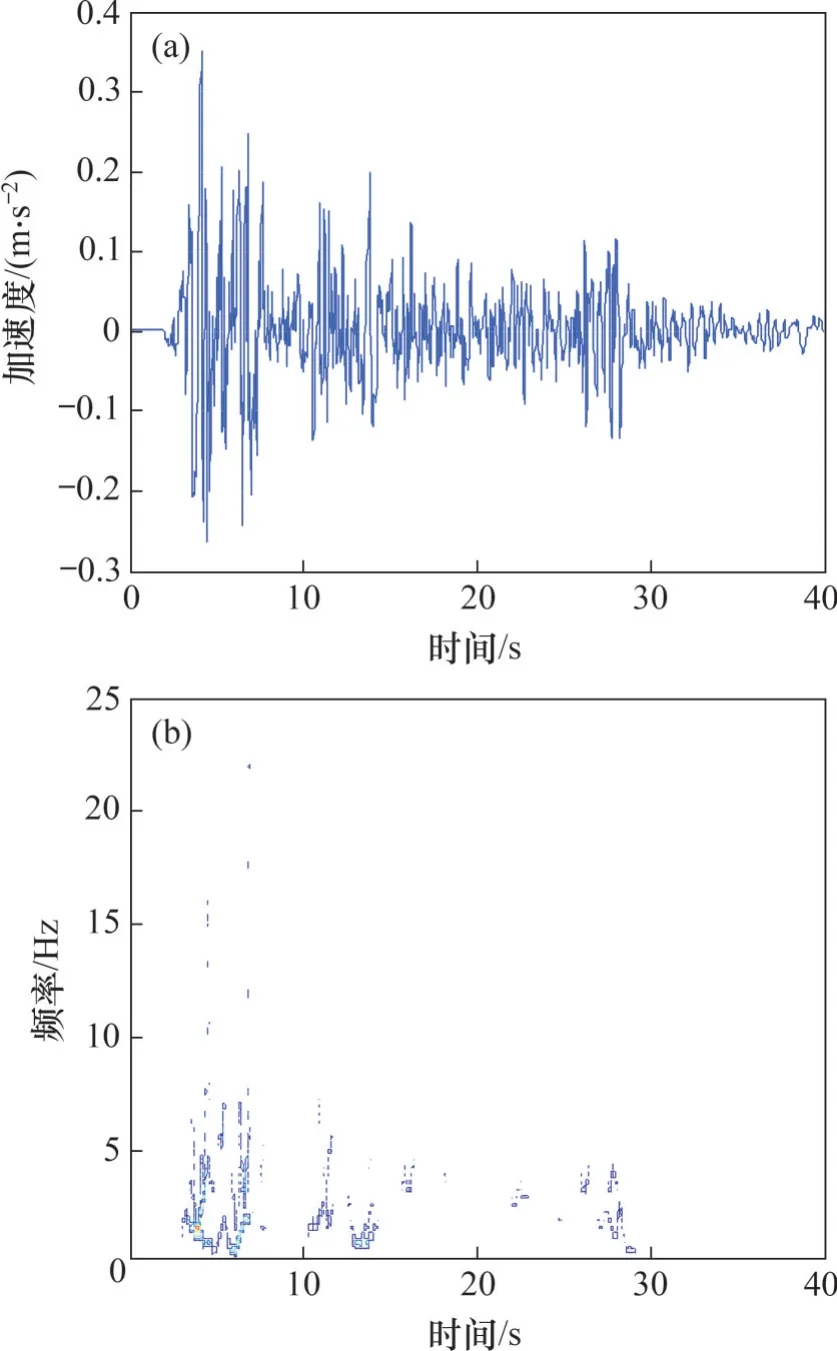
图2 El Centro地震加速度时程和正交Hilbert时频谱Fig.2 Recorded El Centro earthquake accelerogram and its orthogonal Hilbert spectrum

2.2 与目标反应谱兼容的地震动时程合成

假定某建筑物抗震设防烈度为7度，场地类别为Ⅱ类，设计地震分组为第1 组，考虑罕遇地震作用，根据GB 50011—2010“建筑抗震设计规范”确定目标反应谱，如图3所示。

选择目标反应谱的80 个频率控制点，设定拟合误差精度为5%，以El Centro地震动加速度时程作为种子地震动，采用图1所示时变功率谱迭代调整方法，使调整后的地震动时程反应谱以设定的精度拟合目标反应谱。

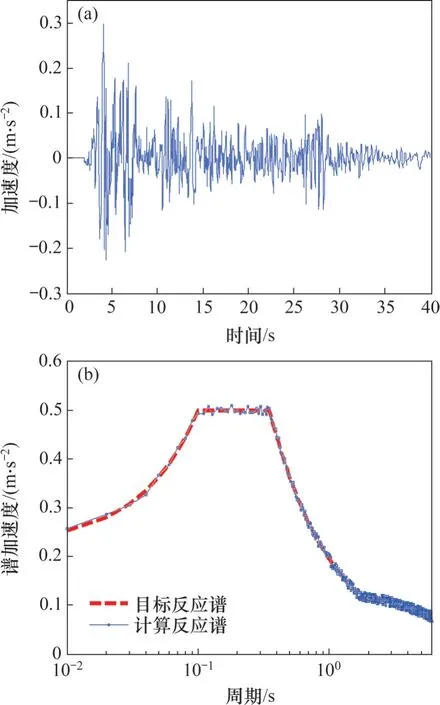
图3 基于El Centro地震加速度调整的地震动时程及其反应谱Fig.3 Adjusted earthquake ground motion and its response spectrum based on El Centro earthquake acceleration

图3(a)所示为采用El Centro地震加速度作为种子时程，经调整后的地震动时程，该地震动时程的计算反应谱与目标反应谱的拟合结果见图3(b)。从图3(b)可以看出：在短周期(0.01～0.10 s)和长周期(0.40～6.00 s)，调整后的地震动时程反应谱与目标反应谱较吻合，拟合效果较好。在中等周期(0.10～0.40 s)范围内，由于地震动能量在该分布范围较弱，可供迭代调整的数据量较少，故调整后的地震动时程反应谱存在“奇点”，经过多次调整之后虽然仍无法收敛，但拟合精度满足要求。

2.3 输入地震动时程方案设计

为研究地震动时频非平稳特性对框架结构非线性响应的影响，设计了4种输入地震动时程。

1)地震动时程1。采用2.2 节基于El Centro 地震加速度时程调整的地震动时程如图3(a)所示。

2)地震动时程2。仅考虑地震动强度非平稳特性，采用式(10)所示三段式强度包络函数在时域内对平稳随机过程进行调整。

式中：t1和t2分别为地震动的振幅上升和下降的起始时间；T为地震动的总持续时间；c为峰值衰减系数。参数t1和t2分别取El Centro地震加速度记录的5%和75%Arias 强度对应的时间，即t1=6.28 s，t2=16.56 s，峰值衰减系数c=0.10，采用图1所示的时变功率谱迭代调整方法调整时程，使其与目标反应谱兼容。调整后的地震动时程如图4(a)所示，时程的计算反应谱与目标反应谱的拟合结果如图4(b)所示。

3)地震动时程3。利用HHT方法提取El Centro波的时频特性，根据演化谱理论合成人工地震动样本，并采用图1所示的时变功率谱迭代调整方法调整时程，使其与目标反应谱兼容。调整后的地震动时程如图4(c)所示，时程的计算反应谱与目标反应谱的拟合结果如图4(d)所示。

4)地震动时程4。利用正交HHT 方法提取El Centro波的时频特性，根据演化谱理论合成人工地震动样本，并采用图1所示的时变功率谱迭代调整方法调整时程，使其与目标反应谱兼容。调整后的地震动时程如图4(e)所示，时程的计算反应谱与目标反应谱的拟合结果如图4(f)所示。

2.4 时程拟合结果分析

图3(a)以及图4(a)，(c)和(e)所示分别为4 种输入地震动方案的时程曲线。从图3和图4可以看出：地震动时程1，3 和4 的波形与El Centro 原始记录波形相似；而地震动时程2的波形与El Centro原始记录波形相差较大。图3(b)及图4(b)，(d)和(f)所示为4种时程的计算反应谱与目标反应谱拟合结果，可以看出各时程的计算反应谱都能与目标反应谱较吻合。

图5所示为输入的4 种地震动时程的正交Hilbert时频谱。对比图5和图2(b)所示El Centro原始记录的正交Hilbert时频谱可以发现：

图4 输入的地震动时程及其反应谱拟合情况Fig.4 Inputted earthquake ground motions and their calculated response spectra

1)对El Centro地震波时变功率谱迭代调整后，得到与反应谱兼容的地震动时程1，其很好地保留了El Centro地震波的时频特性。

2)基于三段式强度包络函数生成的仅考虑强度非平稳特性的地震动时程2，其能量在时频上分布较均匀，主要分布在0～20 s 时间段和0～5 Hz 频率段内，未能有效地反映El Centro 地震动的时频非平稳特性。

3)采用基于演化谱和HHT、正交HHT方法合成的地震动时程2和4，经过时变功率谱迭代调整后与反应谱兼容，其能量在时频上的分布与El Centro地震动的时频分布较相似，这2种时程均很好地保留了原始地震动的时频非平稳特性。

图5 输入4种地震动时程的正交Hilbert时频谱Fig.5 Orthogonal Hilbert spectra of four kinds of inputted earthquake ground motions

3 框架结构非线性地震响应分析

为研究地震动时频非平稳特性对框架结构非线性响应的影响，选择层数为7层和15层的2栋钢筋混凝土框架结构，输入上述4种地震动时程，对结构非线性时程进行分析。

3.1 结构模型

模型1为3跨7层钢筋混凝土框架结构，模型2为5跨15层钢筋混凝土框架结构，其立面如图6所示。模型1 和模型2 的底层框架柱截面长×宽为600 mm×600 mm，其余框架柱截面长×宽均为500 mm×500 mm，框架梁截面长×宽均为300 mm×500 mm，现浇板厚度为120 mm。框架结构的柱、梁和板的混凝土强度等级皆为C40，楼面、屋面恒载为4 kN/m2，楼面、屋面活载为2 kN/m2。模型1和模型2的前4阶周期和自振频率如表1所示。

3.2 非线性时程分析结果

采用SAP2000 软件建立框架有限元模型，将上述4种地震动时程作为输入，分别对2个模型进行非线性时程分析，并对模型的楼层最大位移和层间位移进行比较分析。

特别地，以地震动时程1作用下的结构响应计算结果为基准，定义地震动时程2，3，4 与时程1作用下的结构各楼层层间位移相对误差δi(i=2,3,4)，即

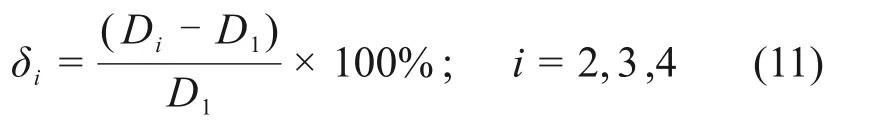
式中：Di为第i个地震动时程作用下框架结构层间位移；D1为地震动时程1 作用下框架结构层间位移。

3.2.1 模型1

图7所示为4 种地震动作用下，模型1 的楼层最大位移曲线。从图7可以看出：

图6 模型1和模型2的立面布置图Fig.6 Elevation layout of model 1 and model 2

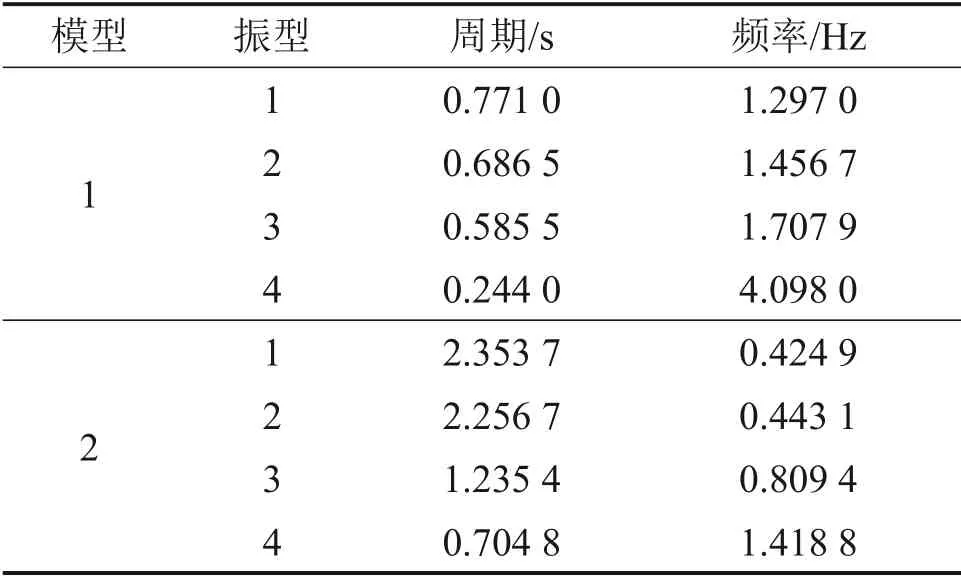
表1 模型1和模型2的前4阶周期和自振频率Table 1 The first four periods and natural frequencies of model 1 and model 2

1)在4 种地震动时程作用下，随着楼层数增加，结构的楼层最大位移增加，且各曲线之间的差距也不断增加，差距在顶层达到最大值。

2)地震动时程2作用下结构的楼层最大位移响应总体上比地震动时程1 作用下的最大位移响应小，其顶层最大位移比地震动时程1作用下的顶层最大位移小5.34%；地震动时程3 和4 作用下结构的顶层最大位移比地震动时程1作用下的顶层最大位移分别增大4.16%和2.82%；地震动时程4 作用下结构的楼层最大位移与基准值最接近，由此表明在基于正交HHT 方法合成的地震动时程与天然地震动时程作用下，框架结构楼层的最大位移响应较一致。

图7 4种地震动作用下模型1的楼层最大位移曲线Fig.7 The maximum floor displacement curves of model 1 under action of inputted four earthquake ground motions

图8所示为4 种地震动作用下，模型1 的各楼层层间位移曲线；表2所示为4种地震动作用下模型1的1～4层层间位移及地震动时程2，3和4与地震动时程1作用下1～4层层间位移相对误差。从图8和表2可以看出：

1)在4种地震动作用下，随着楼层数增加，层间位移均出现先增大后减小的趋势，其中第2层层间位移最大，由此可推断模型1 的第2 层为薄弱层，这与结构第2层柱截面面积减小是一致的。

表2 模型1第1～4层层间位移和相对误差Table 2 Interlayer displacements and relative errors from the 1st to 4th floor of model 1

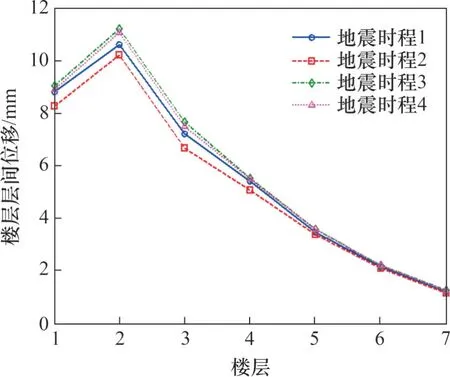
图8 4种地震动作用下模型1的各楼层层间位移曲线Fig.8 Interlayer displacement curves of model 1 under action of inputted four earthquake ground motions

2)在4种地震动作用下，结构各层间位移均呈现以下规律，即时程3、时程4、时程1和时程2的位移依次减小。在地震动时程2作用下，各层间位移最小，其原因在于地震动时程2仅考虑了强度非平稳特征，未考虑频率非平稳特性。由此可见，在结构非线性时程分析中，忽视输入地震动时程的频率非平稳特性可能会低估天然地震动对结构的响应。

3)在4种地震动作用下，结构1～4层的层间位移误差峰值出现在第3层即薄弱层附近；随着楼层增加，各层层间位移误差逐渐缩小。其中，地震动时程2的各楼层层间位移相对误差最大，最大值为-7.43%；地震动时程4的各楼层层间位移相对误差最小，最大值为4.30%；时程3 的各楼层层间位移相对误差介于地震动时程2和4的位移相对误差之间，最大值为6.66%。在地震动时程4 和1 作用下，计算得到的楼层层间位移最接近，由此表明基于正交HHT 方法合成的地震动能更准确地反映天然地震动对结构非线性响应的影响。

3.2.2 模型2

图9所示为4 种地震动作用下，模型2 的楼层最大位移曲线。从图9可以看出：

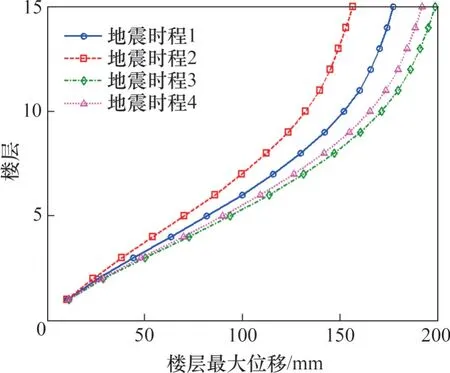
图9 4种地震动作用下模型2的楼层最大位移曲线Fig.9 The maximum floor displacement curves of model 2 under action of inputted four earthquake ground motions

1)在4种地震动作用下，随着楼层数增加，各楼层最大位移迅速增加；在地震动时程1 作用下，模型2 顶层位移为177.42 mm。由此可见，对于高层建筑结构，为满足建筑结构的功能要求和适用性，控制顶层位移至关重要。

2)地震动时程2 作用下的位移最小，为156.48 mm，比地震动时程1 作用下的位移小11.80%；在地震动时程3和4作用下，结构的顶层位移均大于地震动时程1作用下结构顶层位移。在地震动时程4作用下，结构的顶层位移与基准值最接近。对比图7和图9可以看出：模型2 中地震动时程2，3 和4 作用下的顶层位移与基准值的偏差均比模型1中对应的偏差要大，时程2，3和4与基准值的偏差都随着楼层数的增加而增大。

图10所示为4种地震动作用下，模型2的各楼层层间位移曲线，表3所示为4 种地震动作用下，模型2第1～8层层间位移及地震动时程2，3和4与地震动时程1作用下的层间位移相对误差。从图10和表3可以看出：

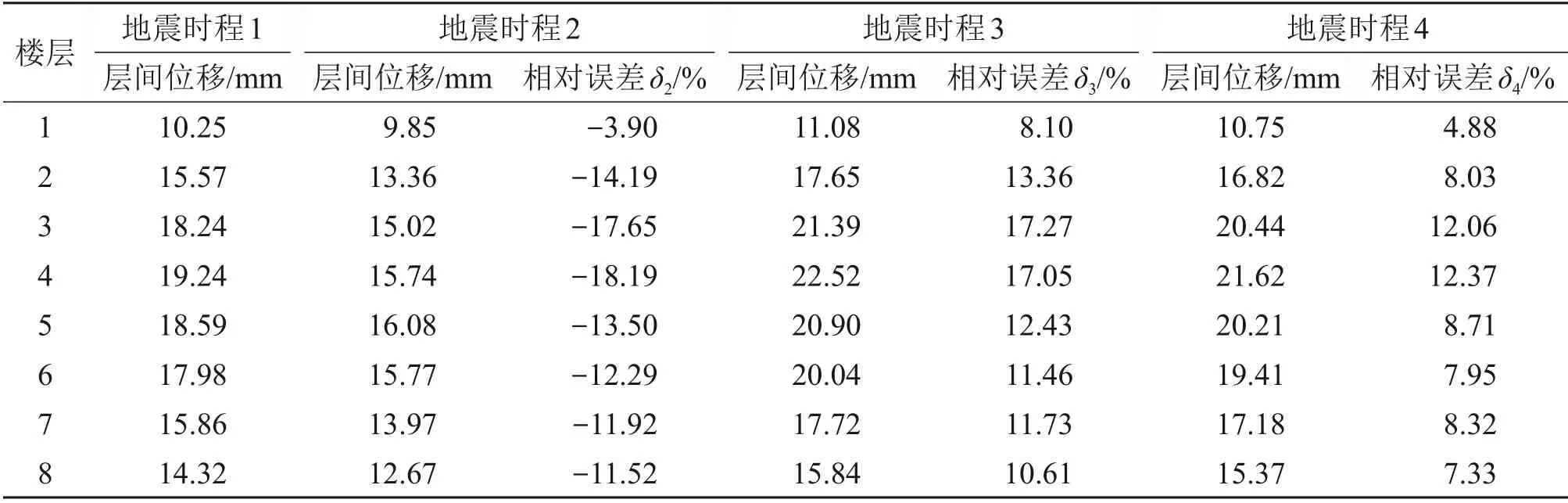
表3 模型2第1～8层层间位移和相对误差Table 3 the interlayer displacements and the relative errors from the 1st to 8th floor of model 2

图10 4种地震动作用下模型2的各楼层层间位移曲线Fig.10 Interlayer displacement curves of model 2 under action of inputted four earthquake ground motions

1)在4种地震动作用下，模型2的各楼层层间位移随层数的增加呈现先增大后减小的趋势，其中，第4 层层间位移最大，可推断模型2 的第4 层为薄弱层。

2)在4种地震动时程作用下，随着楼层层数增加，地震动时程2，3 和4 的各楼层层间位移与基准值的相对误差也呈现先增大再减小的趋势，并且在薄弱层达到最大值。其原因是：结构进入非线性后，地震动的时频非平稳特性对结构响应的影响更加显著，合成的地震动与天然地震动之间的时频特性仍存在差别，这种差别因结构在地震作用下产生局部破坏，材料进入非线性而被放大。其中，在地震动时程4作用下，楼层层间位移与基准值的相对误差最小，为12.37%，这是由于基于正交HHT 方法合成的地震动时程，其时频非平稳特性与天然地震动记录更接近。

图11所示为模型1和模型2的1～7层的层间位移与基准值的相对误差绝对值。从图11可以看出：随着楼层层数增加，地震动时程2，3 和4 与地震动时程1作用下的楼层层间位移相对误差增大；模型1 和模型2 中，地震动时程2 作用下的结构响应均小于地震动时程1作用下结构响应，其原因在于地震动时程2仅考虑了强度非平稳特征，未考虑频率非平稳特性。因此，在结构非线性时程分析中，输入的地震动仅考虑强度非平稳特征，会低估实际地震动对结构的响应，随着建筑高度增加，这种频率非平稳特性对结构地震响应的影响被放大。

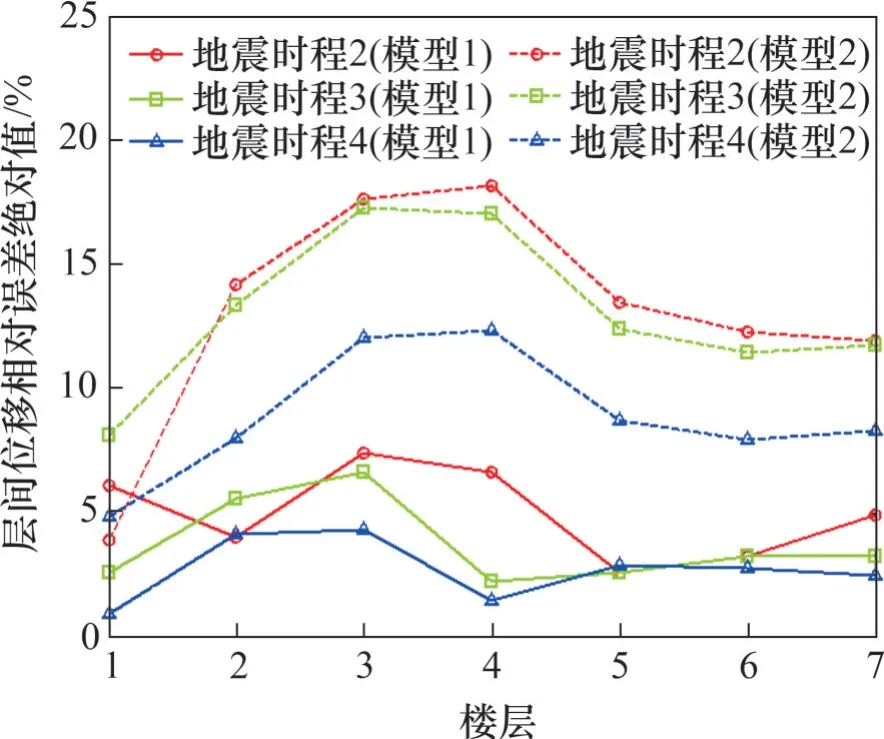
图11 模型1和模型2第1～7层层间位移相对误差绝对值曲线Fig.11 Absolute values of relative error from the 1st to the 7th floor of model 1 and model 2

4 结论

1)基于演化谱和正交HHT 方法的地震动合成方法，通过迭代调整时变功率谱，提出了一种与目标反应谱兼容的地震动合成方法。由该方法合成的地震动时程中，不仅其计算反应谱以一定精度拟合目标反应谱，而且其时频特性与种子地震动时程的时频特性基本一致。

2)基于正交HHT 方法合成的人工地震动能更好地描述天然地震动的时频特性，且框架结构在其作用下的响应与天然地震动作用下的响应最接近。

3)在结构非线性时程分析中，基于强度包络函数生成的人工地震动时程由于仅考虑了强度非平稳特性，未考虑地震动的频率非平稳特性，故存在低估结构响应的问题。因此，采用合成人工地震动作为地震输入时，应考虑地震动的频率非平稳特性，以确保结构安全。