盐渍土地区混凝土加速寿命试验可靠性分析方法

路承功，魏智强，乔宏霞，乔国斌，朱彬荣

(1.兰州理工大学土木工程学院，甘肃兰州，730050；2.兰州理工大学理学院，甘肃兰州，730050；3.东南大学土木工程学院，江苏南京，211189)

与其他土木工程材料不同，混凝土因易于就地取材、造价低廉和可模型好被广泛应用于房屋、道路桥梁和大坝等基础设施建设之中，已成为当今世界用量最大的工程材料[1]。然而在服役地区气候与环境的综合作用下，混凝土可靠性不断降低[2]，耐久性服役寿命往往达不到结构设计要求寿命，不仅带来巨大维修费用，而且造成极大的安全隐患[3-4]。因此，关注混凝土在服役过程中可靠性，对于提升混凝土结构耐久性、安全性及延长服役寿命具有重要意义[5]。

针对混凝土结构在服役过程中耐久性损伤劣化及寿命问题，诸多学者从多方面展开研究。吴彰钰等[6-7]主要研究海洋环境中氯离子侵蚀及海浪冲刷作用，利用可靠度理论及氯离子扩散理论分析混凝土寿命，指出胶凝材料种类、水胶比和保护层厚度对混凝土在海洋环境中的服役寿命影响较大；曾俊杰等[8-10]针对氯离子侵蚀现状，提出用偏高岭土、粉煤灰、矿粉和硅灰等改性辅助胶凝材料改善海洋浪溅区环境中混凝土抗腐蚀性，发现偏高岭土等辅助材料可提高混凝土密实度，提高铝硅比可以抑制混凝土中氯离子的结合量；刘伟庆等[11-12]更关注地下环境中混凝土结构遭受的腐蚀，分析地下混凝土结构随机裂缝宽度、硫酸盐扩散和湿度分布等参数，并依据扩散方程及演化模型预测使用寿命；LIANG等[13-14]考虑了材料、荷载和环境的不确定性，评估干湿循环条件下混凝土可靠性，发现断裂能的均值对可靠性的影响比标准差的更大，但在4 000次干湿循环后影响均不显著；ZHENG 等[15]基于损伤力学与热学理论，提出混凝土耐久性可靠度分析的修正疲劳断裂模型，并评估冻融循环后的损伤状态及剩余寿命；孙博等[16]利用时变概率分析法评定混凝土结构的碳化性能，并通过贝叶斯更新方法，充分考虑模型不确定性对结构碳化结果的影响。

从上述研究中可以看到，有关混凝土材料在服役环境中的耐久性能研究及寿命评估成果丰富，但耐久性研究多考虑1～2个主要损伤因子进行室内试验，寿命评估多基于结构可靠度理论及Fick 定律扩散模型。而实际服役环境中，特别是西部盐渍土地区，在气候和环境的综合作用下，混凝土劣化包含腐蚀盐侵蚀、冻融破坏和干湿循环等多个损伤因子，上述耐久性定量化模型及可靠度分析理论不再适合。基于此，本文从西部盐渍土混凝土实际服役环境出发，设计考虑诸多损伤因子的室内加速试验，并利用Gamma和Weibull分布函数分析混凝土在盐渍土环境中可靠性寿命，找出最佳适用模型，为该地区混凝土耐久性设计及寿命评估提供参考借鉴。

1 试验过程及方案设计

保证失效劣化机理相同的情况下开展室内加速试验，是进行混凝土耐久性研究及寿命评估的重要途径。因此，本文以具有典型盐渍土特性的青海省西宁市腐蚀环境及气候为参照，设计模拟盐渍土地区四季侵蚀的室内人工气候加速试验，加速损伤因子包括复合盐侵蚀、干湿循环、冻融循环及太阳辐射，具体试验制度如图1所示。其中，腐蚀离子包括CO2-3，HCO-3，Cl-，SO2-4和Mg2+，配置复合溶液所需盐包括NaHCO3，NaCl，MgSO4和Na2SO4，其质量分数分别为1.1%，2.2%，3.2%和3.5%，腐蚀盐总质量分数达到10.0%。

试验中成型3种强度等级混凝土所用的配合比如表1所示。水泥为祁连山水泥厂生产的普通硅酸盐水泥，粉煤灰为兰州二热厂生产的Ⅱ级粉煤灰。粗骨料、细骨料及减水剂均由兰州华龙商砼公司提供，级配良好，含泥量等相关指标符合规范要求。试件长×宽×高为100 mm×100 mm×400 mm 的棱柱体，成型后在标准养护室养护。

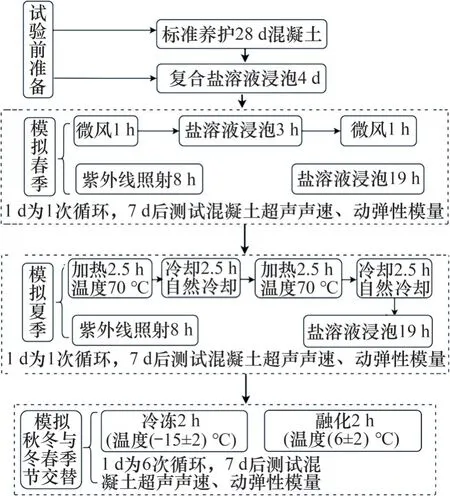
图1 盐渍土地区模拟四季损伤混凝土室内加速试验制度Fig.1 Indoor accelerated test system of simulated four seasons damaged concrete in saline soil area

为更有利于搜集失效数据与判别试件破坏，并最大限度避免每次测量时因仪器等原因对试验结果的影响，参考文献[17]，归一化处理的超声声速损伤评价参数ξa及动弹性模量损伤评价参数ξb，追踪评价混凝土耐久性能，并采用2类损伤评价参数搜集混凝土试件在综合因子作用下的寿命。基于超声声速的损伤评价参数ξa及基于动弹性模量损伤评价参数ξb如式(1)～(2)所示：

式中：Vt和Et分别为一定暴露周期后混凝土的超声声速和动弹性模量；V0和E0分别为初始时刻混凝土的超声声速和动弹性模量。当ξa和ξb介于0～1之间时，认为试件出现损伤劣化；当ξa和ξb大于1时，认为混凝土试件失效破坏。

表1 混凝土配合比及物理性能Table 1 Mix proportion and physical properties of concrete

2 耐久性试验

将收集得到的超声声速及动弹性模量代入式(1)～(2)，得到不同加速周期下混凝土损伤评价参数，如图2所示。由图2(a)可见：随着循环周期增加，3类混凝土ξa呈波动式上升变化，且在28 d后ξa增加速率更快。表明混凝土在太阳辐射、干湿循环、冻融循环及多种腐蚀性盐综合作用下的耐久性能发生较大损伤。这主要是加速试验后期，各种损伤因子相互促进，产生的温度应力、膨胀应力、胀缩应力和盐结晶应力引起混凝土内部微孔孔壁拉裂，原本独立的微孔开始贯通，从微裂纹发展成为微裂缝，甚至形成内外贯通的较宽裂缝。此外，整个加速试验过程中，腐蚀离子在干湿循环及紫外线照射产生的动力作用下，源源不断向混凝土内部迁移运动，与水化产物发生化学反应，生成膨胀产物，产生较大的膨胀应力，加快了裂缝的形成与发展。其中，水化铝酸钙为在硫酸钙存在时生成膨胀应力极大的钙矾石晶体，该晶体因结合32个水分子，体积可增大2.5倍。而混凝土强度主要来源的水化硅酸钙与溶液中的Mg2+发生置换反应，生成无胶凝性的水镁石，极大破坏水泥石的化学组成。胶凝材料溶解析出，导致骨料分离，混凝土内部疏松、溃烂，黏结性能下降，更容易在胀缩应力及温度应力作用下产生裂纹和裂缝；溶液中还有HCO3-和SO2-4等腐蚀性阴离子，不断消耗、固化水泥水化产生的氢氧化钙，生成碳酸钙和硫酸钙等腐蚀产物，导致Ca2+不断释放，出现脱钙现象。在2种腐蚀产物同时存在时生成既无胶凝性，又有膨胀性的碳硫硅钙石，损伤劣化越来越严重。因而，混凝土内部密实度不断下降，超声声速降低，进而ξa快速增大，损伤劣化程度加剧。C30，C40 和C50 这3 类混凝土分别在42，84及105 d附近损伤度达到1.0，表明试件出现破坏。

由图2(b)可见：C30 混凝土的ξb波动性最大，而C40和C50混凝土波动性较小，且C50混凝土的ξb基本呈线性增加，表明C50混凝土在盐渍土多因素作用下的抗侵蚀能力最好，这与水泥水化形成的孔隙结构及凝胶材料的胶凝性有关。对比2类损伤度评价参数，可以看到，基于超声声速的损伤度变化更剧烈，其敏感性更强，表明混凝土内部孔隙密实度处于不断地变化之中。从ξb的变化可知：分别在49，63 及105 d 左右时C30，C40 和C50这3类混凝土破坏试件的损伤度达到1.0，表明试件出现破坏。

3 可靠性建模

3.1 可靠性模型理论

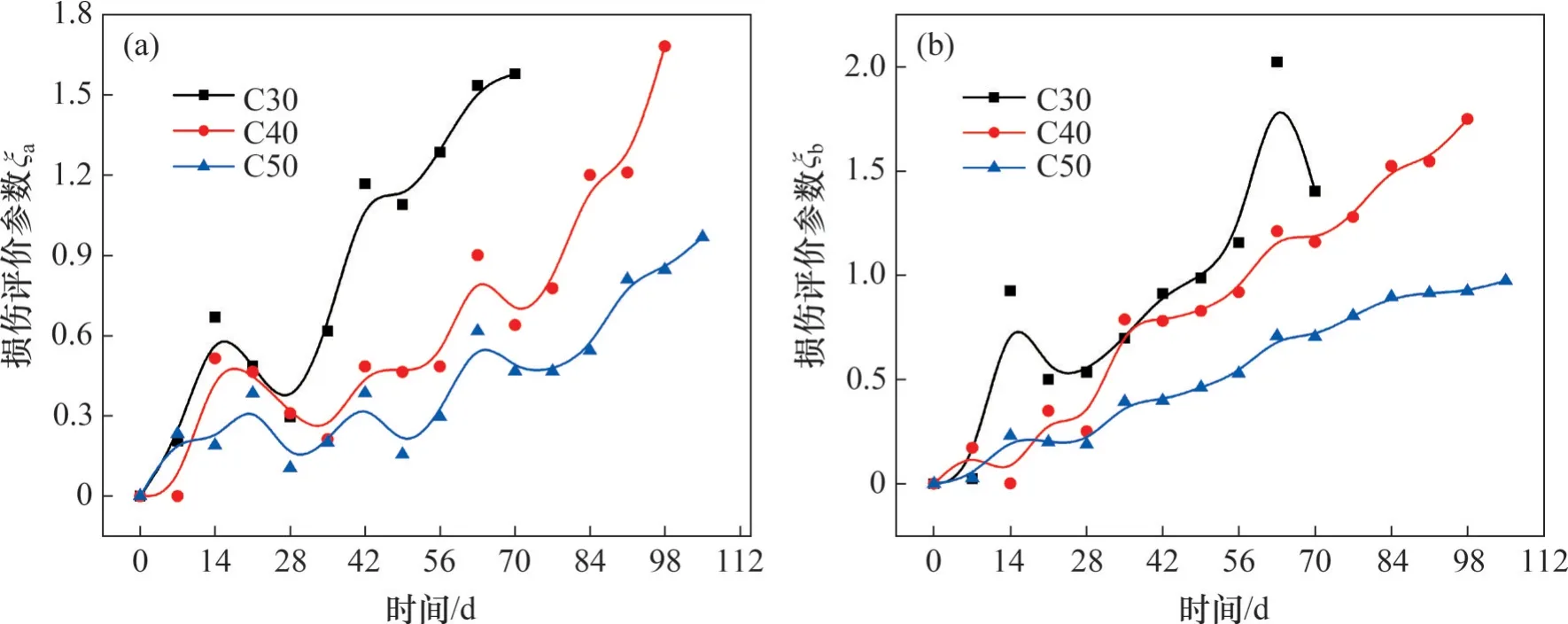
图2 混凝土损伤评价参数Fig.2 Damage evaluation parameters of concrete

产品可靠性分析最早始于20世纪20年代，用以评价分析产品在规定服役环境和时间内完成预定功能的概率，且初期主要针对军工产品。随着计算机科学的发展及可靠性理论的不断深入，开始在机械设备、航天器、车辆和电子仪器等方面应用，并取得了良好效果[18]。可靠度是可靠性分析中衡量产品无障碍工作最显著的指标，其计算主要依据数理统计及概率论极限状态方法[19]。Weibull分布和Gamma分布均是可靠性领域十分重要的分布函数[20-21]，然而Gamma 分布具有较复杂的密度函数和生存函数，且参数估计较困难，应用范围不及Weibull 分布，特别是在混凝土寿命评估方面。

以较成熟的2 参数Weibull 分布模型为基础，对比分析3参数Weibull分布模型和Gamma分布模型在混凝土可靠性评估方面的适用性。其中2参数分布模型有形状参数与尺度参数2类参数，形状参数主要影响分布曲线形状，其值不变时，表明混凝土失效机理不变。尺度参数主要影响曲线在时间轴上的离散程度，其值越大，表明混凝土在加速试验环境中所得寿命越不集中。3参数分布模型则在2参数模型的基础上增加位置参数，可直观表示混凝土失效的初始时间。

假设混凝土在模拟盐渍土加速环境中所得寿命t服从Gamma 分布，α为形状参数，β为尺度参数，则其密度函数为：

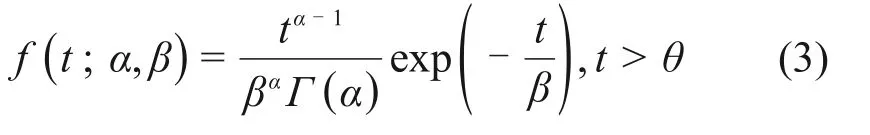
式中：γ(α，t/β)为不完全Gamma 函数，且γ(α,t)=

与Gamma 模型函数表达不同，假设位置参数为δ，则3参数Weibull模型的分布函数、密度函数分别如式(5)～(6)所示，当位置参数为0时，即可转变为2参数Weibull分布。

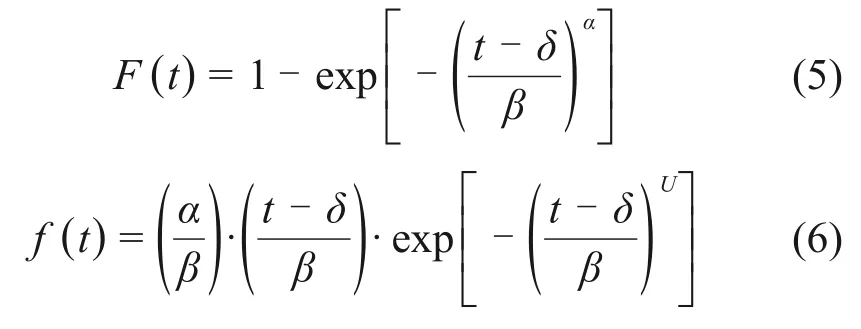
相应的可靠度R(t)及失效率λ(t)可通过分布函数及密度函数求得，其相互之间关系如式(7)～(8)所示：

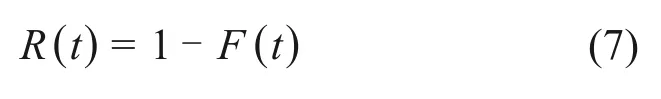
3.2 模型先验假设检验

对室内加速试验中所得混凝土寿命数据预先进行Weibull分布和Gamma分布检验，通过概率分布图中样本点与变换后所选分布拟合直线的离散程度进行预先判定。在检验中确定显著性水平为0.05，利用SPSS 统计分析软件得到具有95%保证率的概率检验图，如图3所示。从图3可见：寿命样本点基本分布在所选分布拟合直线95%置信区间之内，且C30 寿命样本点位于概率图最左的位置，而C50混凝土位于最右位置，较好反映了混凝土寿命数据符合所选分布。为更精确判定寿命样本点是否符合相应的分布，采用K-S检验法进行判定，不同混凝土检验结果如表2所示，从表2可以看到：K-S值均高于0.05显著性水平，表明各寿命样本点均服从Gamma分布及Weibull分布。

图3 可靠性模型假设检验图Fig.3 Test chart of reliability model hypothesis

表2 不同可靠度模型K-S检验值Table 2 K-S test values of different reliability models

3.3 可靠性模型参数估计

通过Gamma分布及Weibull分布函数评估混凝土可靠性，还需利用寿命样本进行参数估计。结合分布函数形式，采用极大似然法对Gamma 分布及2 参数Weibull 分布进行参数估计[22]。该法主要利用密度函数及样本信息，通过构造似然函数进行参数估计，是统计学中最经典的参数估计方法。当似然函数一阶导数为0时，所求参数即为参数估计值，其Gamma分布及2参数Weibull的似然函数一阶导数分别如式(9)～(10)所示。

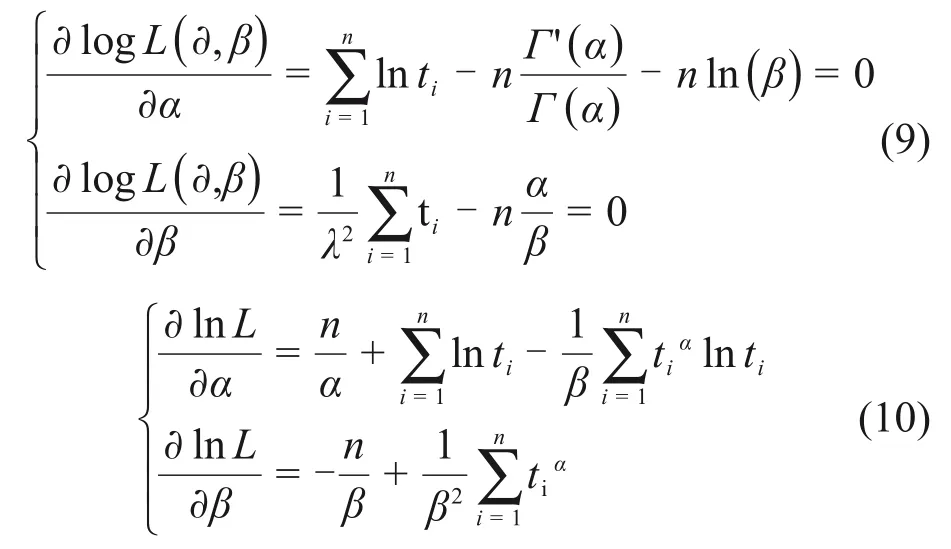
式中：n为样本容量；i代表样本中第i个寿命数据。

通过求解式(9)～(10)便可得Gamma 分布及2 参数Weibull 分布参数估计值。3 参数Weibull 分布因其具有3个未知参数，构造似然函数进行求解时需求解一个非线性方程组，变量多，难度大，因此，参考文献[23]，采用易于理解计算的相关系数优化法进行参数估计。不同分布模型下参数估计值如表3所示。

4 混凝土可靠性寿命评估

4.1 Weibull分布模型和Gamma分布模型

将表3所得参数估计值代入式(3)～(8)，通过Matlab 计算得到不同损伤劣化时间下2 参数Weibull分布与Gamma分布的可靠度、密度及失效率，如图4所示。

表3 各分布模型下混凝土参数估计值汇总Table 3 Summary of concrete parameter estimates under each distribution model

由图4(a)可见：不同强度混凝土基于Gamma分布、2参数Weibull分布的可靠度曲线均呈2个阶段变化。第1阶段可靠度高，且混凝土强度等级越高，在第1阶段的持续时间越长；第2阶段可靠度持续降低，表明混凝土性能损伤加剧，直至失效。对比2类分布可靠度曲线，3类混凝土基于Gamma分布的曲线在第1阶段持续时间均略长，在第2阶段的下降速率相对更快，得到的可靠度寿命也较长。C30，C40和C50混凝土基于Gamma分布的可靠性寿命分别约为1 239，2 239和2 869 h，而基于2 参数Weibull 分布的可靠性寿命分别为1 207，2 211和2 838 h。

分布函数的密度曲线可以很好地描述单位时间“产品”失效的概率，从图4(b)观察到：3 类混凝土密度曲线呈较对称的峰值，峰值处可靠度降低的加速度最大，混凝土强度等级越高，峰值出现的时间越迟。C30，C40和C50基于Gamma分布的密度峰值出现时间分别为1 046，2 058和2 645 h，而基于2 参数Weibull 分布的峰值出现时间分别为1 086，2 095 和2 692 h。基于Gamma 分布的密度曲线峰值明显较基于2 参数Weibull 分布的峰值更早地出现，但2类分布密度曲线峰值差异较小，其中C30混凝土峰值几乎相同，而C40和C50混凝土峰值略有差异。

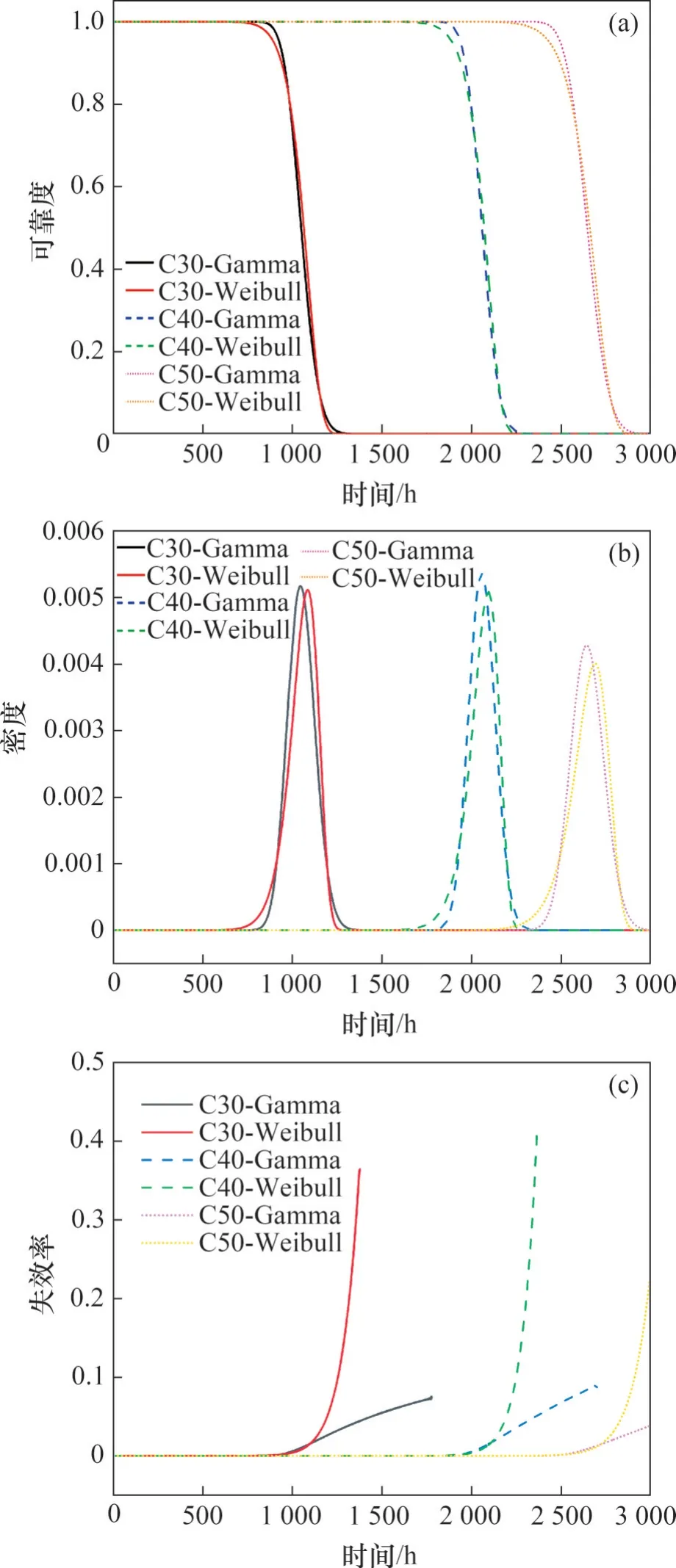
图4 Gamma与2参数Weibull分布可靠性曲线Fig.4 Reliability curve of Gamma and two-parameter Weibull distribution

失效率直接反映产品在某种加速环境中失效速度。从图4(c)观察到：3 类混凝土初期失效率极小，随着时间延长，失效速率显著增大，除部分时刻外，2 参数Weibull 分布的失效率曲线均高于Gamma 分布失效率曲线。且后期2 参数Weibull 分布失效率增加速率远远大于Gamma 分布的失效增加速率。相同失效率下，强度等级越高，所需时间越长，其失效速率越慢。

4.2 2参数Weibull模型和3参数Weibull模型

为充分对比分析Weibull 分布的参数数目对混凝土可靠性寿命分布的影响，分别选用2 参数Weibull 分布和3 参数Weibull 分布模型分析混凝土加速寿命样本，将表3中2种模型的参数估计值代入相应函数，得到2 参数Weibull 分布和3 参数Weibull 分布模型的可靠度寿命曲线、密度曲线及失效率曲线如图5所示。

从图5(a)可见：2 种参数模型下，3 类混凝土基于Weibull 分布的可靠度寿命曲线下降段差异较小，但第1阶段的差异较大，其第1阶段的持续时间明显不同。且2 参数Weibull 模型可靠度曲线在第1阶段与第2阶段的过渡处更平稳，可靠度随时间有一个较缓慢的降低过程，而3 参数Weibull 模型从第1阶段向第2阶段过渡时更迅速，拐点位置更明显，可靠度一旦出现下降，就以极快速率降低。其中C30，C40和C50混凝土2参数Weibull可靠度曲线第1阶段的持续时间分别为804，1 790和2 304 h，而3参数模型可靠度曲线第1阶段的持续时间分别为917，1 964和2 508 h。可以看到，3参数模型在第1阶段持续时间较2参数模型增加110～200 h。至可靠度完全降至为0 时，即混凝土完全破坏时的可靠性寿命对于2 类Weibull 模型也略有差异。当可靠度下降至0.2 以下时，3 参数Weibull模型的可靠度曲线一直在2 参数Weibull 模型的上方，其可靠性寿命较2 参数模型可靠性寿命长。C30，C40 和C503 类混凝土基于2 参数Weibull 模型的可靠性寿命分别约为1 207，2 212 和2 838 h，而基于3 参数Weibull 模型的可靠性寿命分别约为1 294，2 400和2 960 h。

由图5(b)可见：2类基于Weibull分布模型的密度曲线差异较大。其中，2 参数Weibull 模型的密度曲线基本呈单峰对称状，而3 参数Weibull 模型密度曲线对称性不佳，其左侧密度曲线上升极快，右侧密度曲线下降较缓慢。同时观察到3类混凝土密度曲线中，3 参数模型的密度曲线峰值较2 参数模型密度曲线峰值出现较早，即2 参数Weibull 模型密度曲线峰值相较3参数Weibull模型更偏右。

图5 2参数Weibull与3参数Weibull分布可靠性曲线Fig.5 Reliability curves of two-parameter Weibull and three-parameter Weibull distribution

从图5(c)可见：2 类模型下混凝土失效率在初期极小，基本为0，表明混凝土失效的概率小。随着时间延长，3 类混凝土失效率增加较快，尤其2参数Weibull 模型失效率增加速率更快。后期3 类混凝土的2 参数模型失效率均比3 参数模型的高，且以幂次形式增加，而C40和C50混凝土3参数模型失效率在阶跃式上升后失效率增加速率有所减缓，C30混凝土失效率以直线增加，均不同于2参数模型的失效率幂次增加。考虑到混凝土后期失效特点，2 参数模型失效率变化特点更符合实际状况。

4.3 3类模型可靠性结果对比

结合上述结果，同时对比2 类Weibull 分布模型与Gamma 分布模型可以观察到，3 参数Weibull分布模型与2 参数Weibull 分布模型、Gamma 分布模型相差较大，其可靠度曲线从第1阶段向第2阶段过渡时较迅速，密度曲线对称性不强，失效率曲线后期以直线增加一段时间后又以较低速率增加。Gamma 分布与2 参数Weibull 分布最接近，可靠度曲线在过渡阶段更平缓，密度曲线更对称，失效率曲线后期以较快速率增加。3 类模型中，2参数Weibull 分布在第1 阶段的持续时间最短，可靠度完全降为零时的可靠度寿命最小，失效率在加速试验后期以幂次型增加，更符合混凝土在多损伤因子作用下的损伤劣化机理。且2 参数Weibull 分布模型参数估计更简便，工程适用性更强。

为更好对比混凝土在3类可靠性分布模型下降段中可靠度与时间的关系，整理各可靠性分布模型在部分可靠度水平下的可靠性寿命，如表4所示。由表4可见：在可靠度为0.2～0.6的区间，3类混凝土2 参数Weibull 分布模型的可靠性寿命均较其他2类模型的高。结合耐久性分析中混凝土加速寿命，可靠度水平为0.4附近时，可靠性寿命最接近各强度混凝土加速寿命。该可靠度水平既为混凝土寿命预测提供了重要的结束标志，也符合混凝土结构材料有关安全储备的要求。

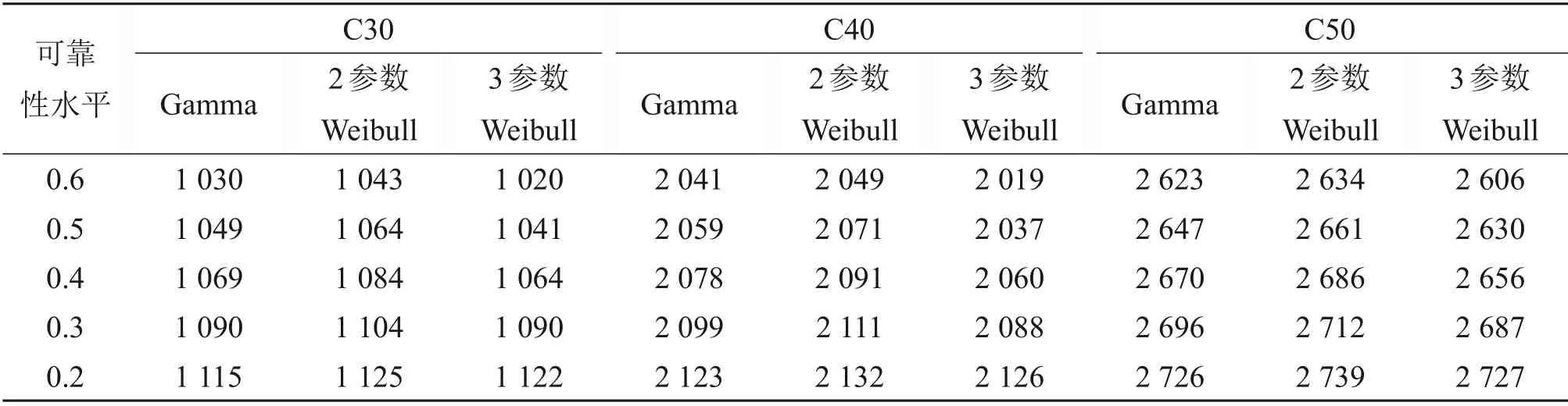
表4 不同可靠度水平下Weibull、Gamma模型可靠性寿命Table 4 Reliability life of Weibull and Gamma models under different reliability levels h

5 结论

1)Gamma分布与Weibull分布均可以很好地拟合模拟混凝土盐渍土地区多损伤因子作用下的室内加速试验寿命样本，两者概率分布图具有较高拟合精度。

2)3 参数Weibull 模型可靠度从第1 阶段向第2阶段过渡时较迅速，密度曲线对称性不强，失效率曲线后期以直线增加一段时间后又以较低速率增加。

3)Gamma 分布与2 参数Weibull 分布最接近，可靠度曲线在过渡阶段更平缓，密度曲线更对称，失效率曲线后期均以较快速率增加。

4)3 类分布模型中，2 参数Weibull 在第1 阶段的持续时间最短，可靠度寿命最小，在加速试验后期，失效率以幂次型增加，更符合混凝土在多损伤因子综合作用下的劣化规律，且2 参数Weibull 分布模型参数估计更简便，工程适用性更强。

5)可靠度水平为0.4时，可靠性寿命最接近混凝土加速寿命，该可靠度水平可作为盐渍土地区多损伤因子作用时混凝土寿命结束标志，也符合混凝土结构材料有关安全储备的要求。